[Linear Algebra] Subspace of Rn

Subspace of Rn

Rn에 set H가 subspace이면 다음 세 가지 조건을 만족한다.
a) The zero vectors is in H
b) H에 임의의 벡터 u와 v가 있을 때, u+v는 H에 있다.
c) H에 임의의 벡터 u와 스칼라 c가 있을 때, 벡터 cu는 H에 있다.

• 조건 b와 c는 덧셈과 스칼라 곱에 닫혀있다.
• Rn에 zero vetors는 zero subspace이다.
  

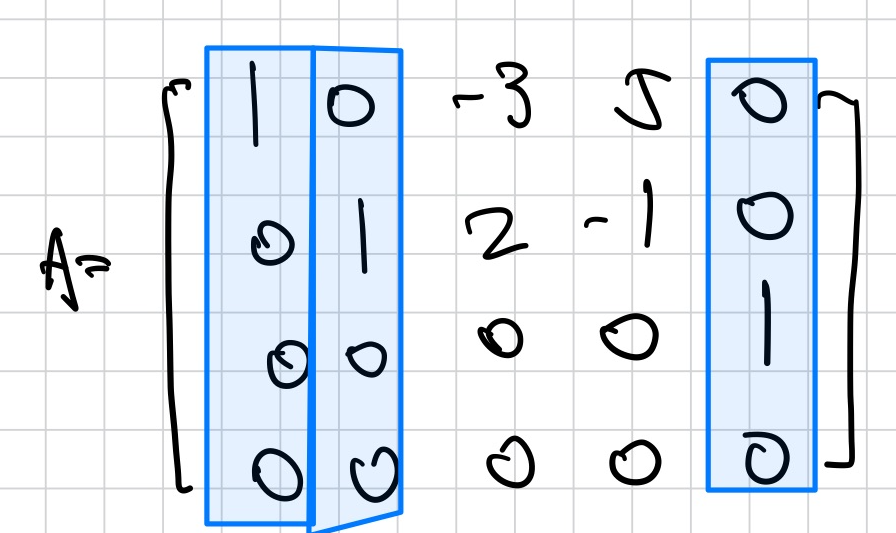
Column Space

matrix A의 column space는 A의 column의 모든 linear combination set이다.

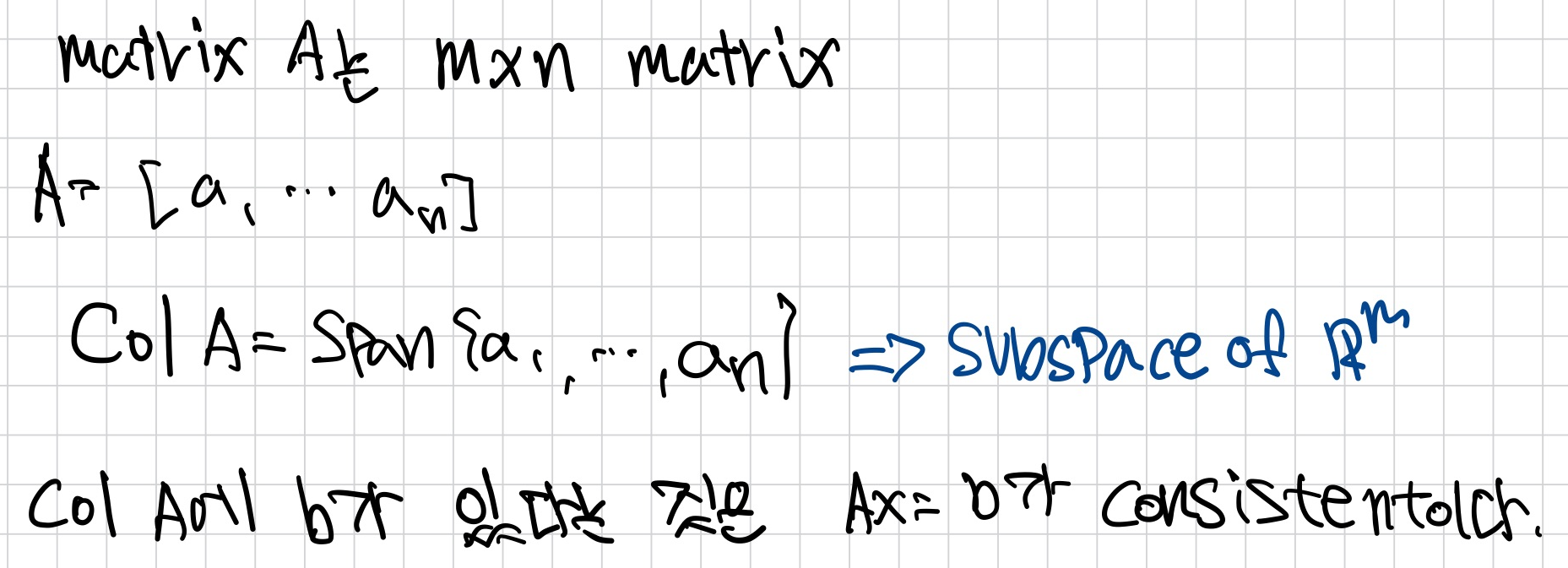
Null Space

matrix A의 null space는 Ax=0의 모든 솔루션이다.

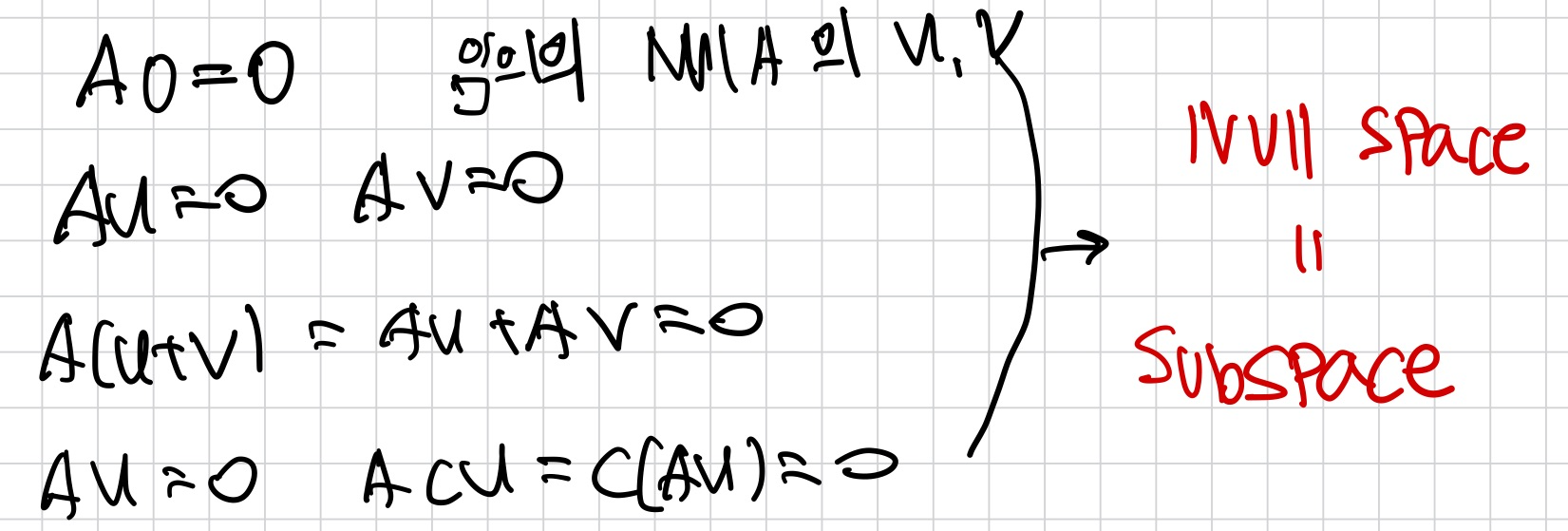
• null space는 implicitly(암시적)으로 정의
• column space는 explicitly(명시적)으로 정의

Basis for a subspace

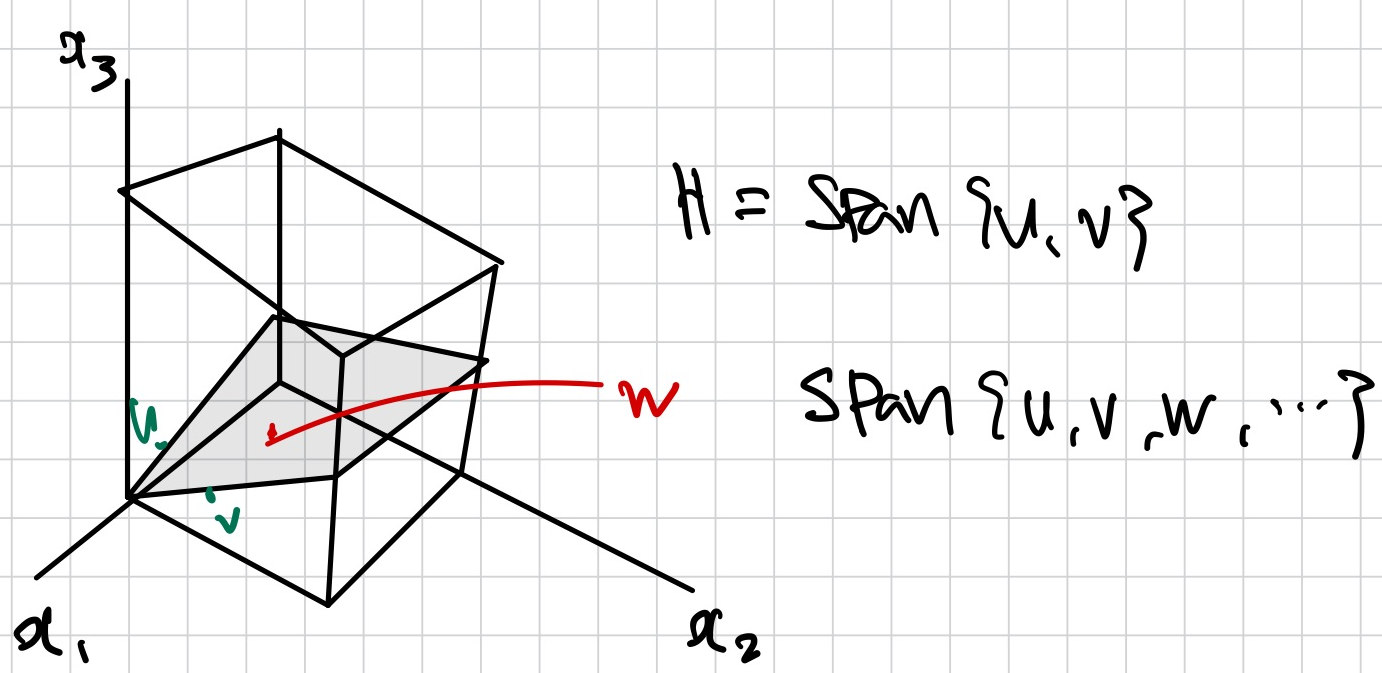
그림의 W처럼 무수히 많은 벡터를 Span할 수 있음
따라서 Rn에서 subspace H의 basis는 linearly independent한 span H set이다.

Standard Basis for Rn

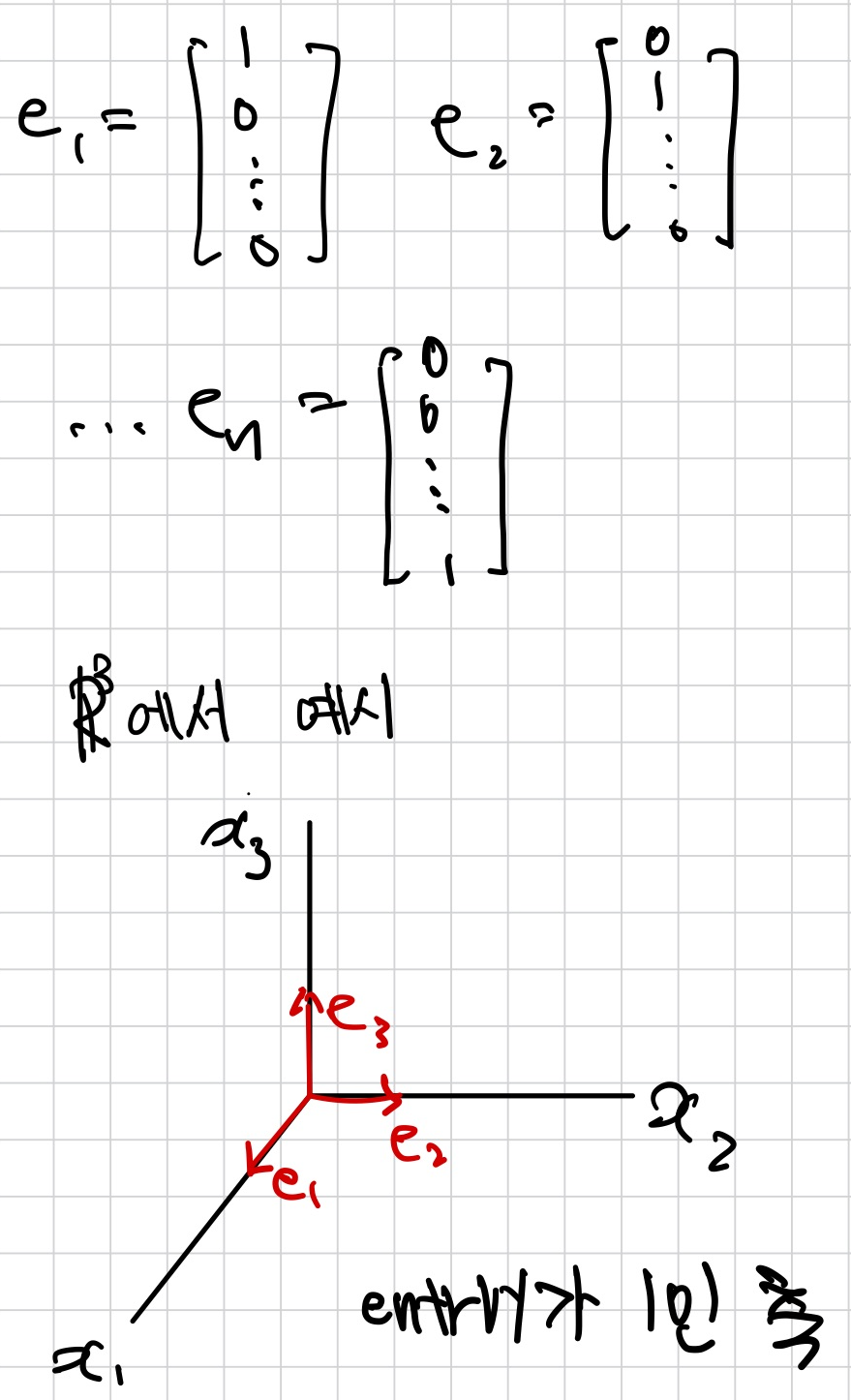
Theorem.

matrix A의 pivot column은 A의 column space의 basis이다.

• ex)