[Linear Algebra] Invertible Matrix / Partitioned Matrix

Characterizations of Invertible Matrices

A가 n x n square matrix이다. 다음은 equivalent하다.

• A는 invertible matrix이다.
• A는 In에 row equivalent이다.
• A x=0은 trivial solution을 갖는다.
• A는 n pivot positions을 갖는다.
• CA=I 를 만족하는 n x n matrix C가 있다.
• DA=I 를 만족하는 n x n matrix D가 있다.
• A의 컬럼은 Rn를 span한다.
• A x=b은 Rn에 b에 대해 적어도 하나의 solution을 갖는다.
• A의 컬럼은 linearly independent이다.
• linear transformation T(x)=A X는 onto이다.
• linear transformation T(x)=A X는 one-to-one이다.
• AT는 invertible matrix이다.

Invertible Linear Trasnformations

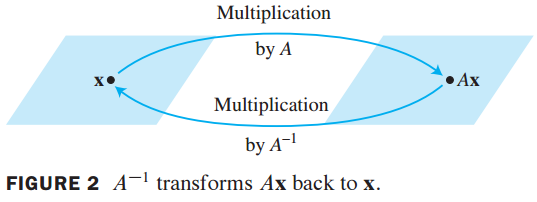
이미지 출처 : Invertible linear transformation

다음 수식을 만족하는 S : Rn → Rn이 있다면 linear transformation T: Rn → Rn은 invertible하다.

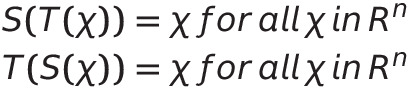
T : Rn → Rn가 linear transformation이고 A가 T에 대한 standard matrix이다.
T가 invertible, A는 invertible matrix인 것은 동치이다.
이 경우, linear transformation S는 S(x) = A-1x로 주어진다.

partitioned Matrix

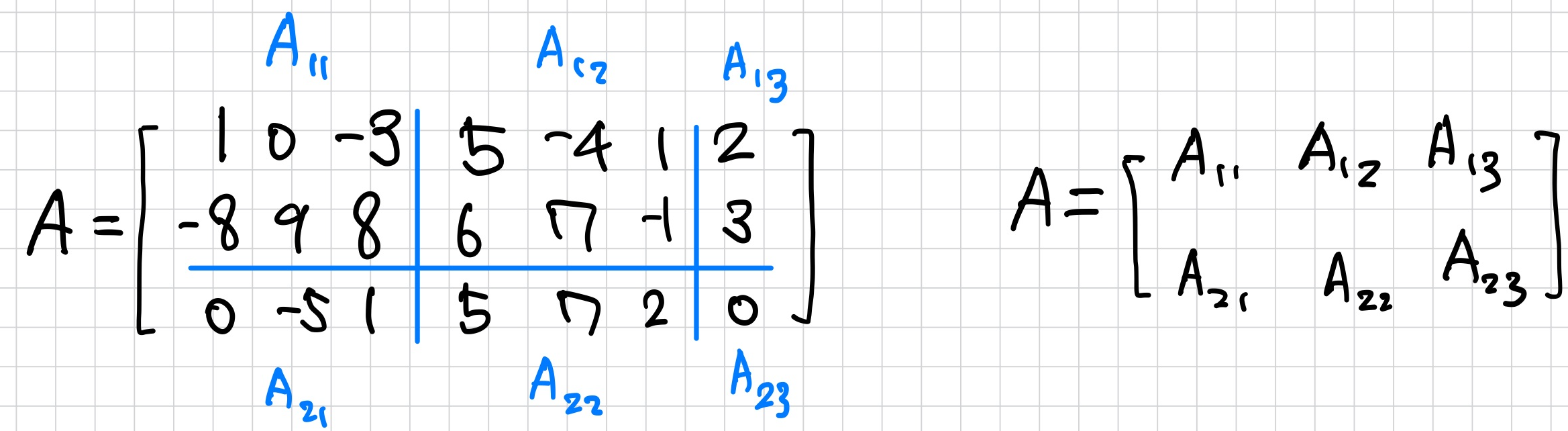
Multiplication of Partitioned Matrices

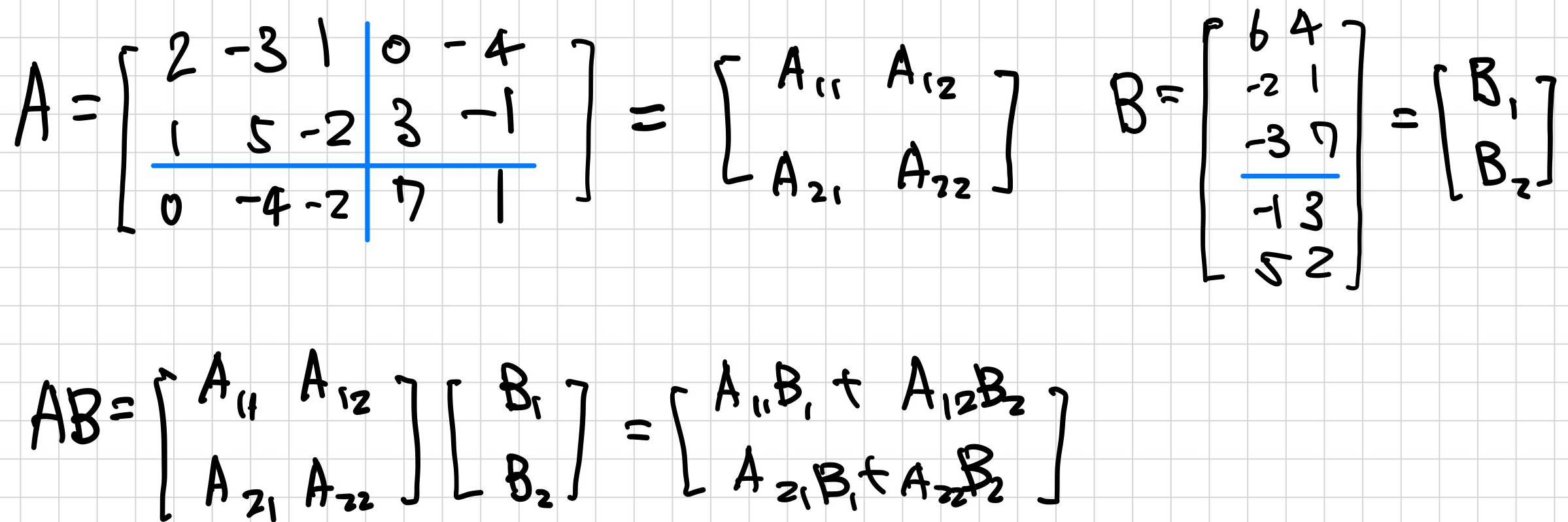
A와 B처럼 파티션이 나뉘어져 multiplication 연산이 가능한 matrix를 conformable이라 한다.

Column-Row Expansion of AB

matrix A와 B를 row와 column으로 파티션을 나누면 다음과 같이 나타낼 수 있다.

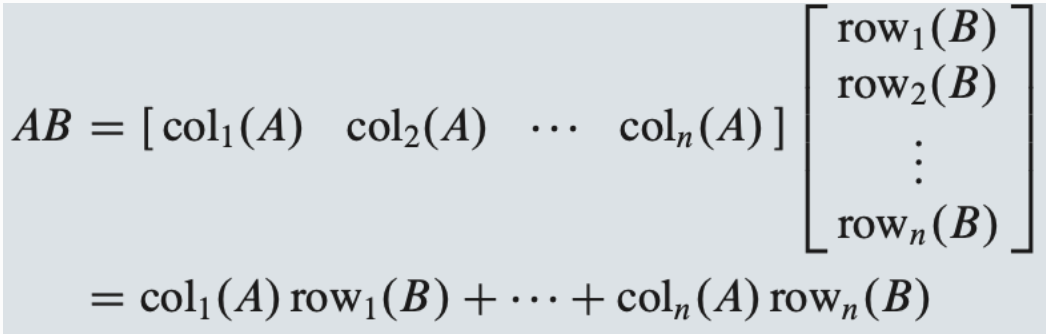
Inverse of Partitioned Matrices

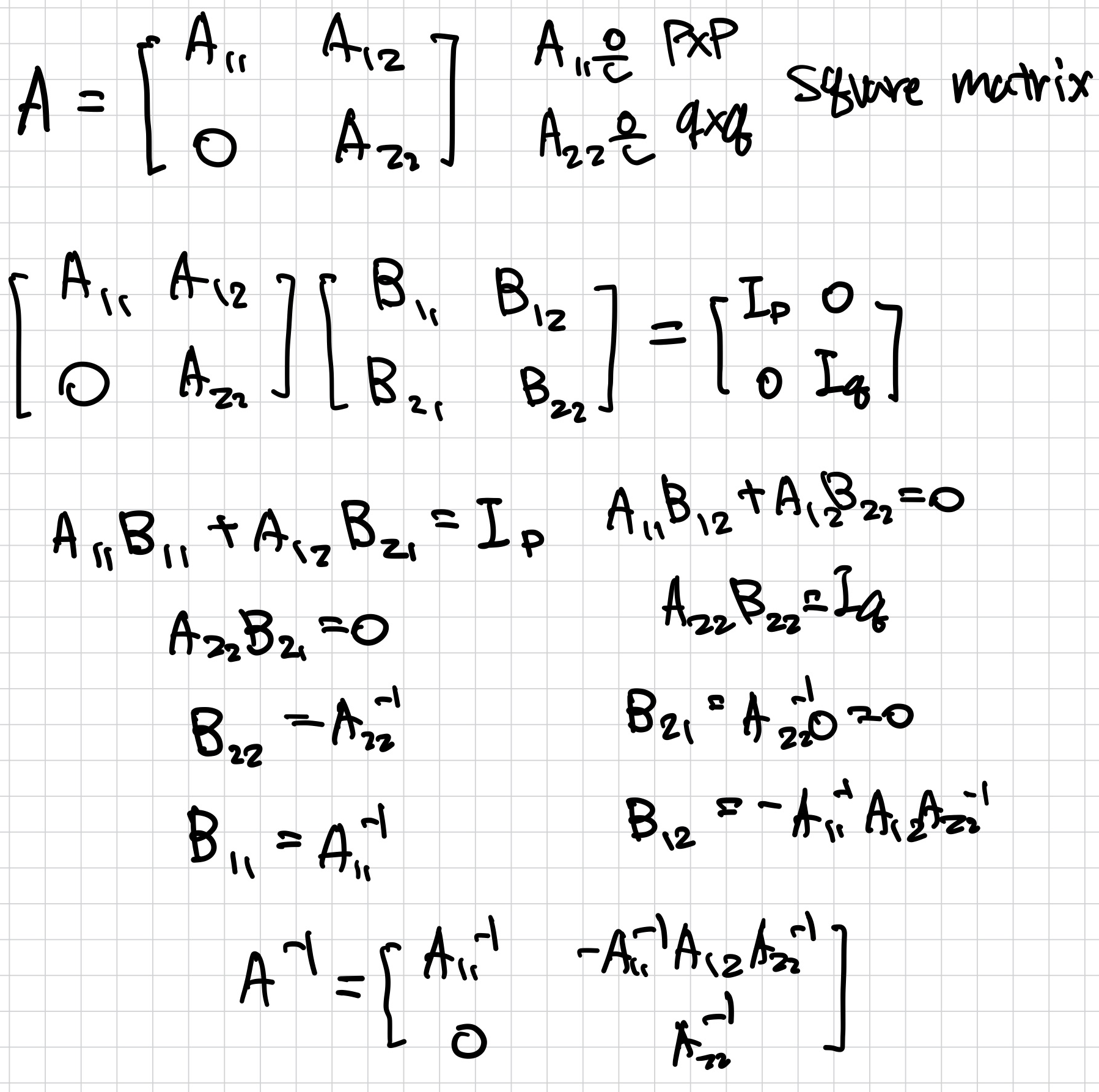
matrix A를 block upper triangular라고 하며, A12가 0이면 block diagonal matrix라고 한다.