[Linear Algebra] The Inverse of a Matrix

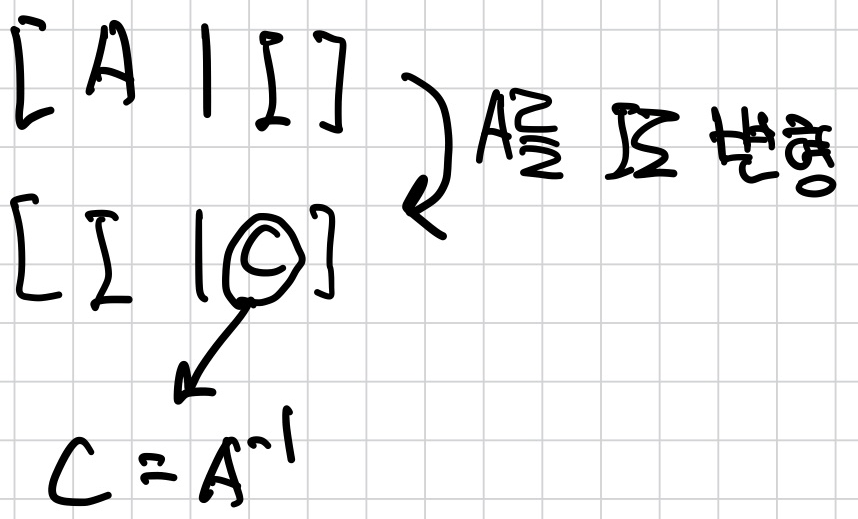
Invertible Matrix

CA=I and AC=I
을 만족하는 matrix C가 존재하면 matirx A는 invertible하다.

• A-1A=I and AA-1=I
• invertible한 matrix → nonsingular matrix
• not invertible한 matirx → singular matrix

Theorem.

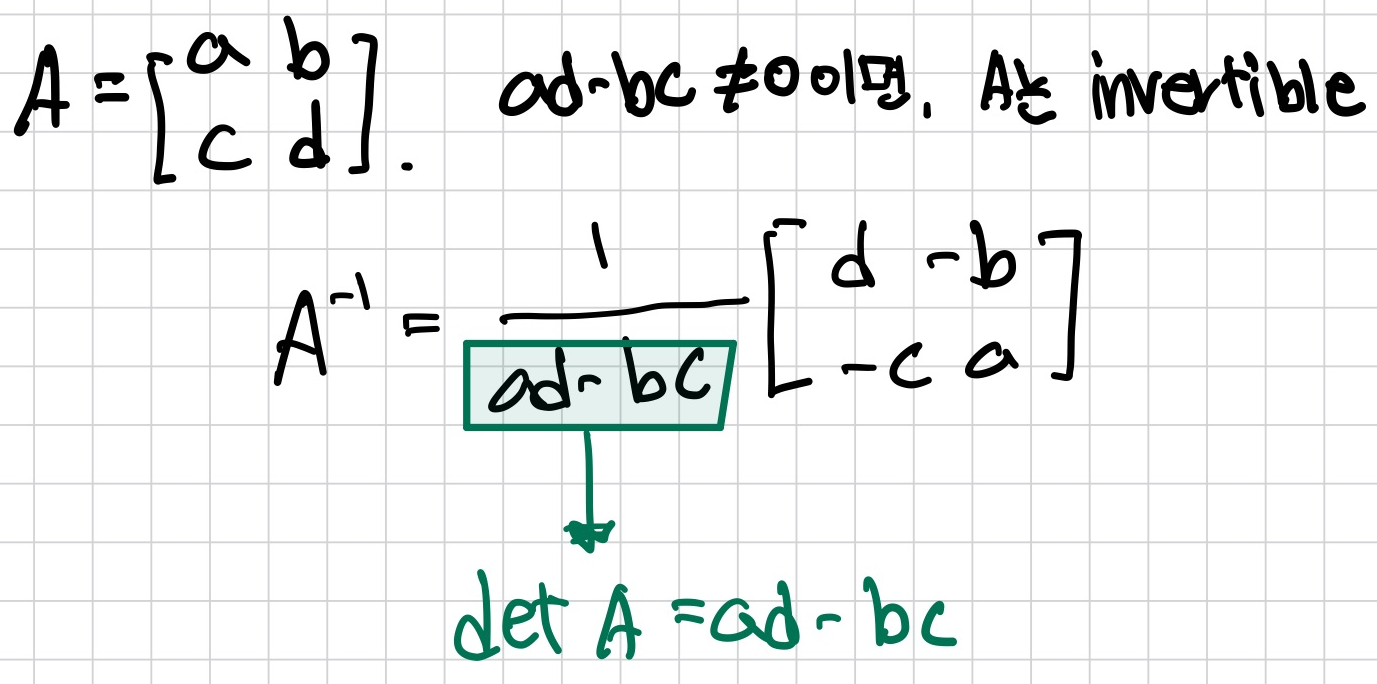
Theorem.

A가 invertible하면 Rn에 b에 대해서 A X=b는 유일한 solution을 갖는다. → X=A-1b

Theorem.

• A가 invertible matrix이면, A-1도 invertible이다.
• A, B가 invertible이면, (AB)-1=B-1A-1 이다.
• A가 invertible이면 AT의 inverse는 (A-1)T이다. → (AT)-1=(A-1)T

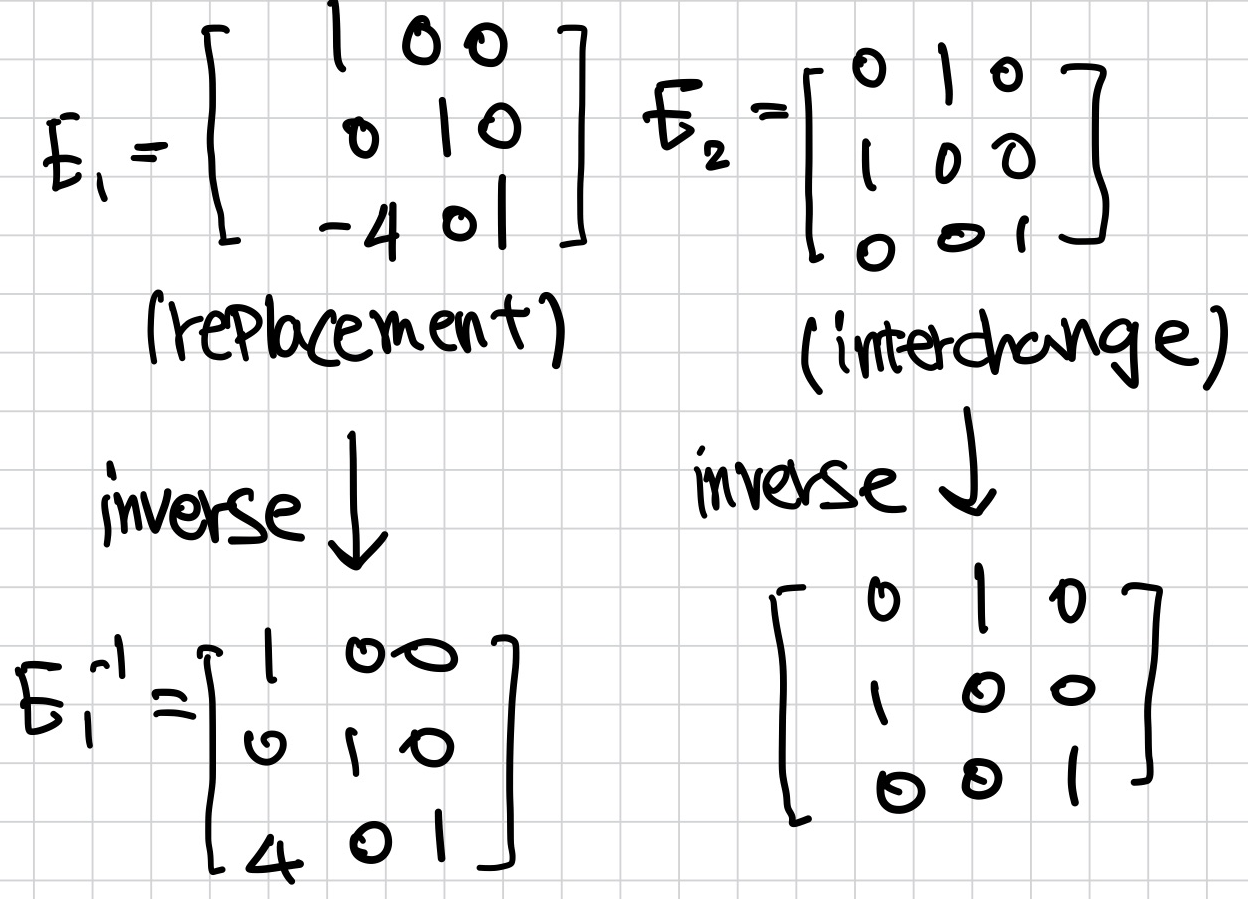
Elementary Matrices

• elementary matrix는 identity matrix에 elementary row operation을 한 번 수행한 matrix이다.
• elementary matirx E는 invertible이며, E의 inverse는 E를 identity matrix로 변형하는 같은 종류의 elementary matrix이다.
  

Theorem.

• n x n matrix A가 invertible, A는 In에 row equivalent는 필요충분조건