[Linear Algebra] Linear Transformation

Transformation

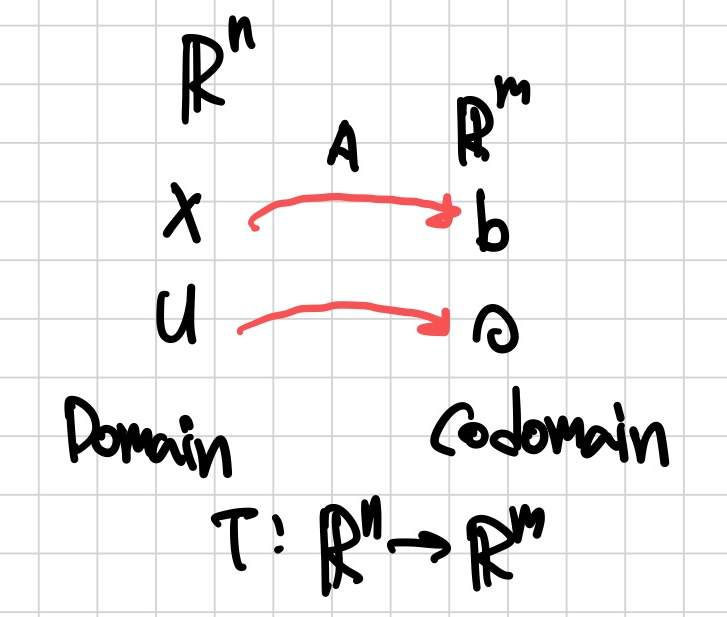
• Rn에서 Rm로 transformation T는 행렬의 곱으로 계산된다.

• Rn에 x가 Rm에 T(x) 벡터로 할당된다.
  

• transformation T가 linear하면
  
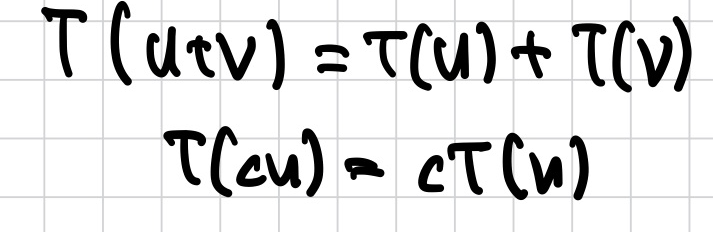
  행렬의 linear 성질과 동일하다.

• Rn → Rm T가 linear transformation일 때
  

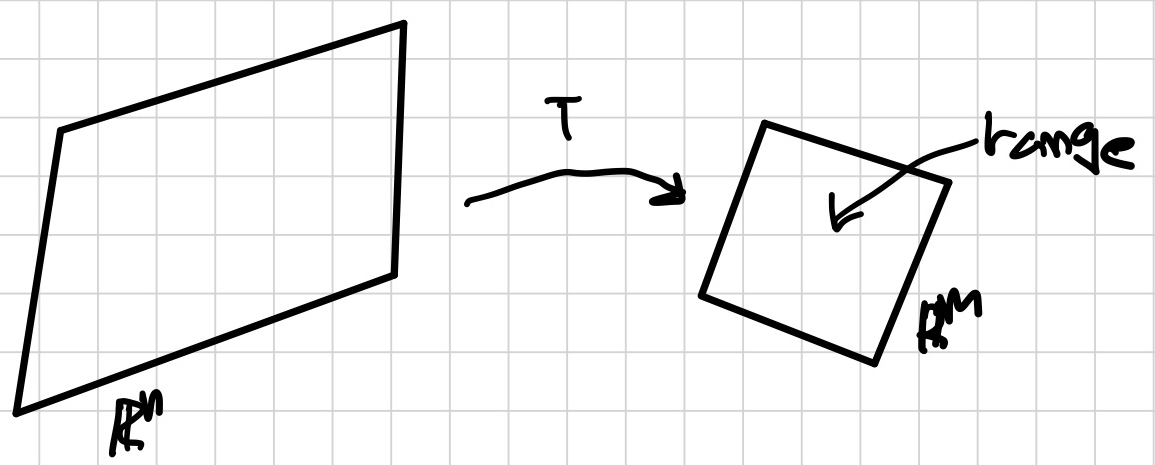
• Onto (T : Rn → Rm)
  Rn onto Rm은 Rn에 x가 Rm에 적어도 하나의 이미지가 있다.
  T(x)=b가 적어도 하나의 solution을 갖는다.
  

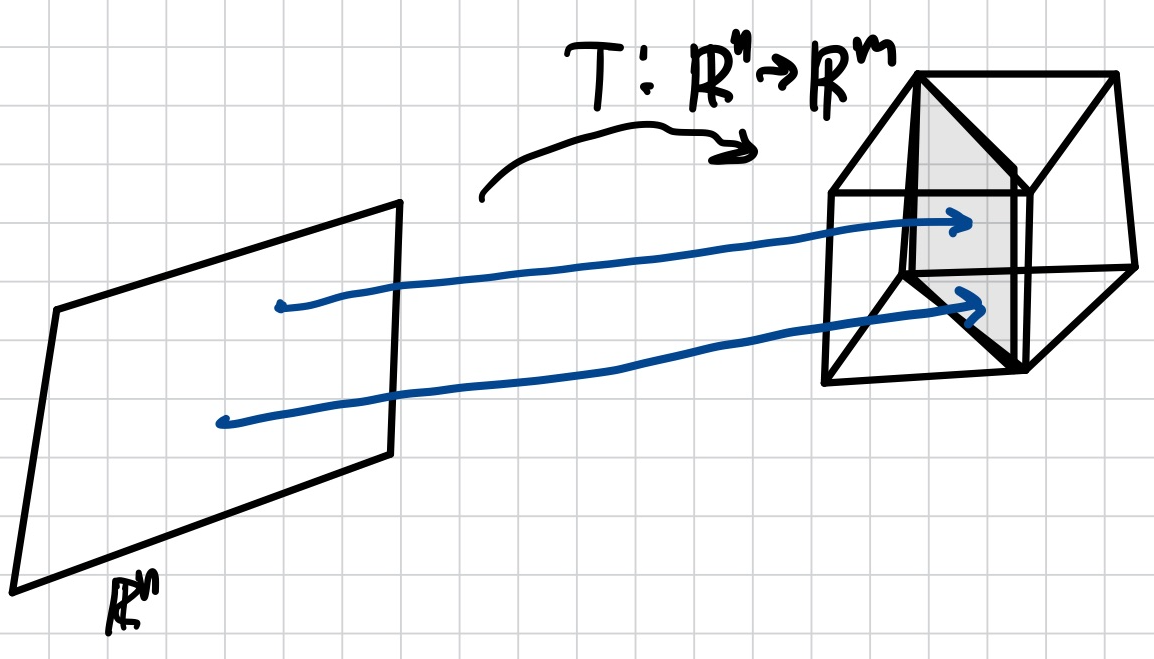
• one-to-one (T : Rn → Rm)
  Rn onto Rm은 Rn에 x가 Rm에 단 하나의 이미지가 있다.
  T(x)=b가 유일한(unique)한 solution 또는 solution을 갖지않는다.
  

• T : Rn → Rm가 linear transformation이면,
  T가 one-to-one, T(x)=0이 trivial solution을 갖는다.