3. Divide and conquer algorithm (1)

dmswl·2025년 10월 11일

algorithm

Algorithm

목록 보기

3/16

3.0 Divide and conquer algorithm

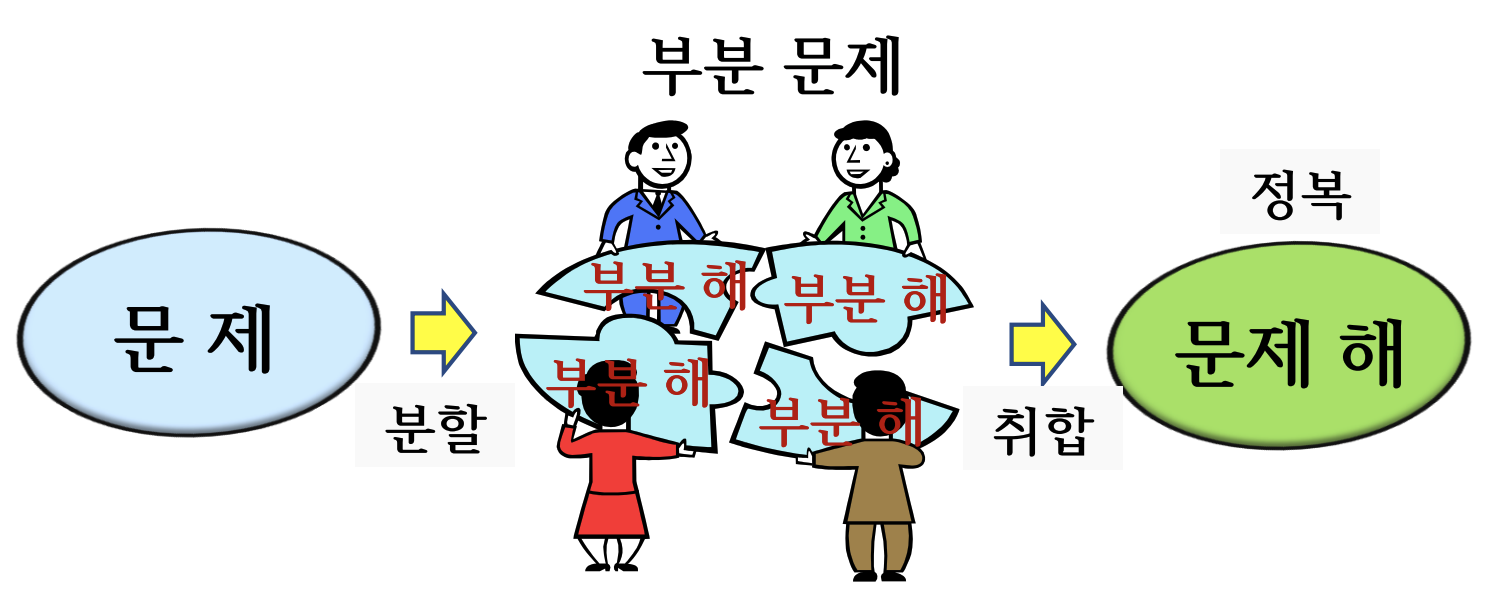
주어진 문제의 입력을 분할하여 문제를 해결(정복)하는 방식의 알고리즘
- 분할(1)한 입력에 대하여 동일한 알고리즘을 적용하여 해 계산(2)
- 이들의 해를 취합(3)해 원래 문제의 해를 얻음
부분 문제와 부분 해
- 분할된 입력에 대한 문제를 부분 문제(subproblem)
- 부분 문제는 더 이상 분할할 수 없을 때까지 분할 or 쉽게 해결 가능할 때까지 분할

3.0.1 Divide

크기가 n인 입력을 3개로 분할하고, 각각 분할된 부분 문제의 크기가 n/2일 경우의 분할 예

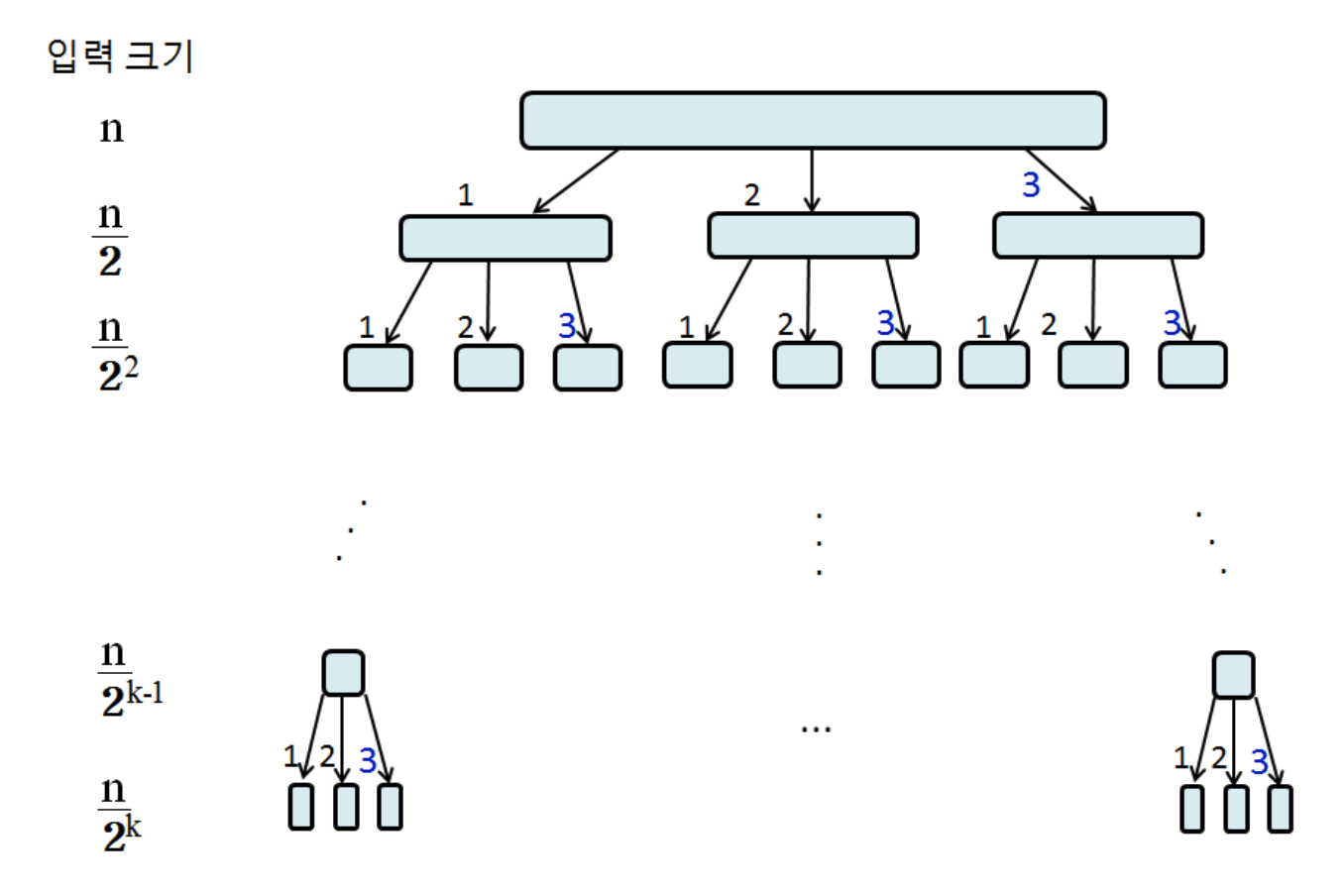
입력의 크기가 n인 하나의 큰 문제를 3개의 작은 문제로 분할
각 작은 문제의 크기는 n/2
이 과정을 계속 반복해서 작은 문제로 만듦
가장 아래쪽으로 가면 $n/2^k$ 까지 쪼개짐

n/2 크기의 문제를 3개씩 만든다.

입력 크기가 n일 때, 총 분할 횟수

총 분할한 횟수 = k라면
1번 분할 후 각 입력 크기 $n/2$
2번 분할 후 각 입력 크기 $n/2^2$
k번 분할 후 각 입력 크기 $n/2^k$
$n/2^k = 1$ 일 때 분할 못함

종료 조건이 문제가 1개만 남는 순간이므로, $n=2^k$ 따라서 $k = log_2n$ 이 된다.

3.0.2 Conquer

대부분의 분할 정복 알고리즘
- 문제의 입력을 단순히 분할만 해서는 못 구함
따라서 분할된 부분 문제들을 정복해야 함
- 부분 해를 찾아야 함
- 일반적으로 부분 문제들의 해를 취합하여 보다 큰 부분 문제의 해를 구함

3.0.3 Kind of Divide and conquer

분할되는 부분 문제의 수와 부분 문제의 크기에 따라서 다음과 같이 분류
문제가 a개 분할, 부분 문제의 크기가 1/b로 감소하는 알고리즘
- a=b=2인 경우: 합병 정렬, 최근접 점의 쌍 찾기, 공제선 문제
- a=3, b=2인 경우: 큰 정수의 곱셈
- a=4, b=2인 경우: 큰 정수의 곱셈
- a=7, b=2인 경우: Strassen의 행렬 곱셈 알고리즘

Quick Sort

문제가 2개로 분할되고, 부분 문제의 크기가 일정하지 않은 크기로 감소하는 알고리즘
- pivot 기준으로 좌우로 나뉨

Binary Search

문제가 2개로 분할되나, 그 중에 1개의 부분 문제는 고려할 필요가 없으며, 부분 문제의 크기가 1/2로 감소하는 알고리즘
- 항상 반씩 나누고 한쪽만 재귀적 탐색

Selection Problem

문제가 2개로 분할되나, 그 중에 1개의 부분 문제는 고려할 필요가 없으며, 부분 문제의 크기가 일정하지 않은 크기로 감소하는 알고리즘

Insertion Sort, Fibonacci

부분 문제의 크기가 1, 2개씩 감소하는 알고리즘

3.1 Merge sort

입력이 2개의 부분 문제로 분할되고, 부분 문제의 크기가 1/2로 감소하는 분할 정복 알고리즘

n개의 숫자들을 n/2개씩 2개의 부분 문제로 분할
각각의 부분 문제를 순환(재귀)으로 합병 정렬
2개의 정렬된 부분을 합병하여 정렬(정복)

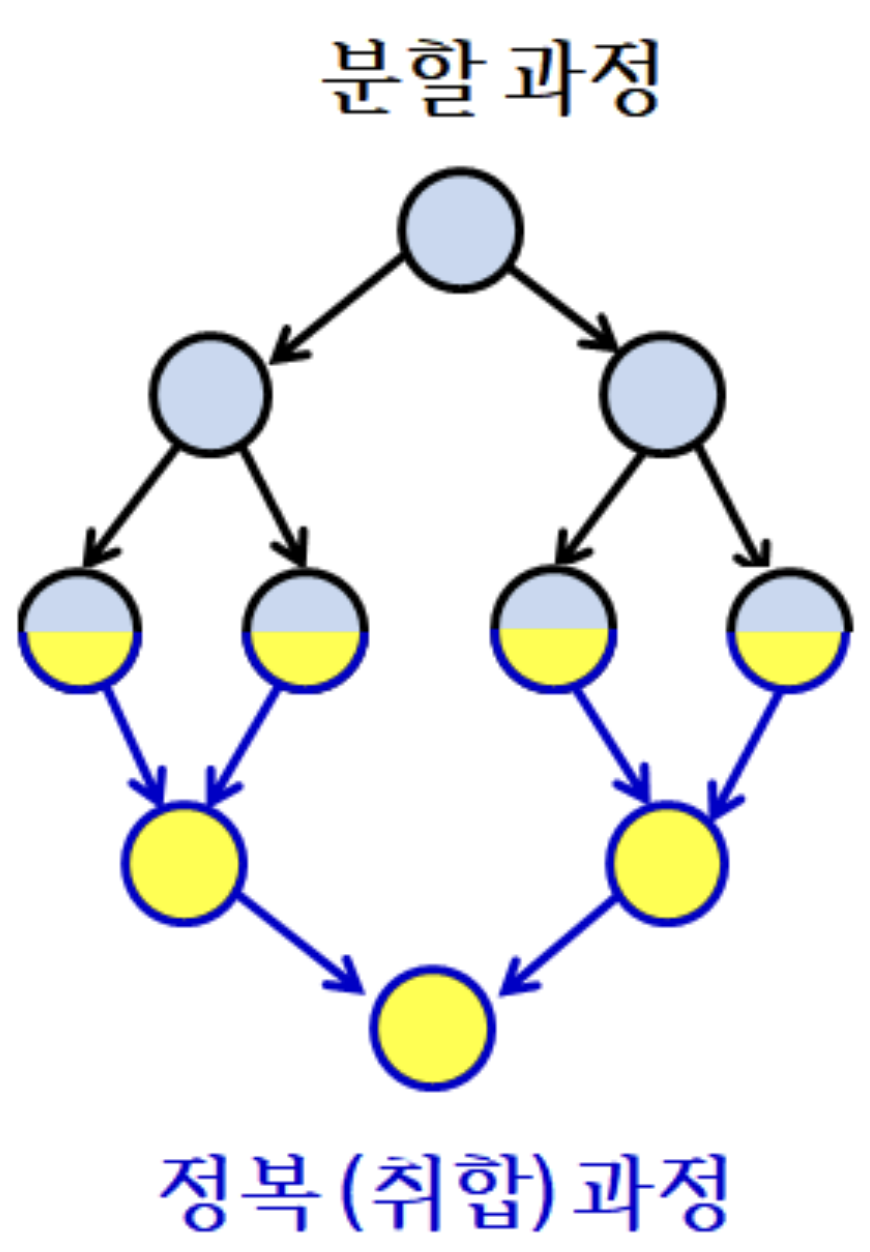
합병 과정이 문제를 정복하는 것
일반적으로 분할정복 알고리즘에서 ‘정복’은 나뉜 하위 문제 각각을 푸는 단계를 의미하고, 그 이후의 ‘취합’ 과정은 별도로 존재할 수 있다. 그런데 합병정렬에서는 두 하위 문제의 “합병” 자체가 곧 상위 문제의 해답을 얻는 정복 단계와 일치한다.

3.1.1 Merge

2개의 각각 정렬된 숫자들을 1개의 정렬된 숫자로 합치는 것

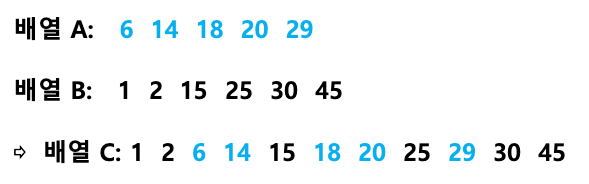
이미 각각 정렬이 끝난 하위 배열 둘을 합치는 것만으로 상위 배열의 정렬이 완성되기 때문에 합병 과정이 문제를 정복하는 것과 같다.

MergeSort(A,p,q)

Input: A[p] ~ A[q]
Output: 정렬된 A[p] ~ A[q]

if (p < q){
$\,\,\,\,$ k = $\lfloor$ (p + q) / 2 $\rfloor$ // 내림
$\,\,\,\,$ MergeSort(A,p,k) // 앞부분 순환 호출
$\,\,\,\,$ MergeSort(A,k+1,q) // 뒷부분 순환 호출
$\,\,\,\,$ A[p] ~ A[k] 와 A[k+1] ~ A[q]를 합병
}

n = 8, A = [37, 10, 22, 30, 35, 13, 25, 24]

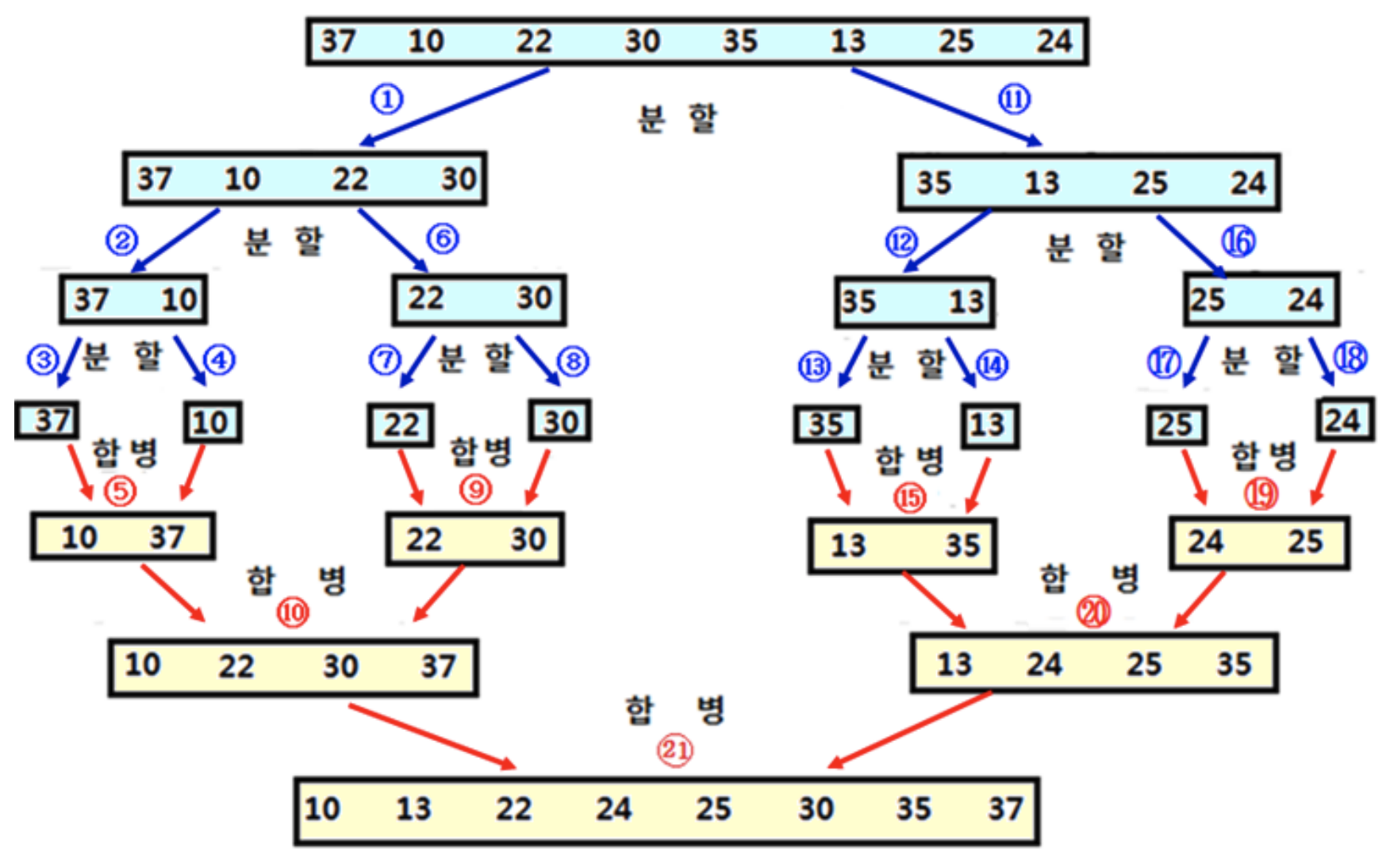
크기가 1이 되면 분할을 멈추고 합병 시작
단계 5에서 2번의 비교 필요 (1) 10과 37 비교하고 10 추가, (2) 남은 37 추가

3.1.2 Time Complexity

분할

분할하는 부분은 배열의 중간 인덱스 계산과 2회의 순환 호출이므로 $O(1)$

합병

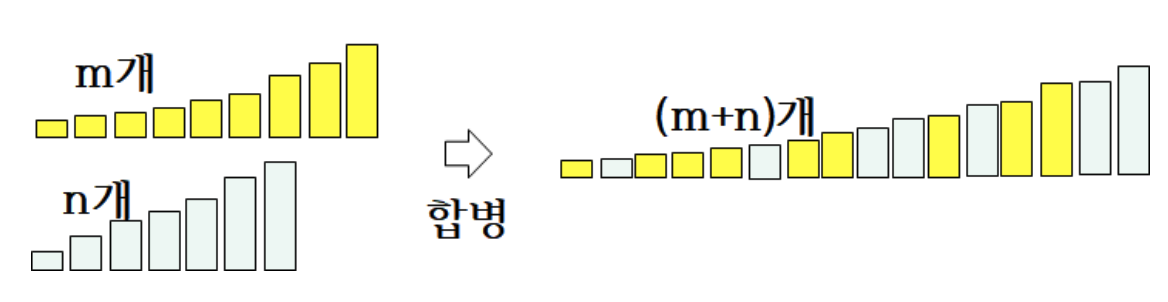
합병의 수행 시간은 입력의 크기에 비례
- 2개의 정렬된 배열 A와 B의 크기가 각각 m과 n이라면, 최대 비교 횟수 $= (m + n -1)$
  - 2개 이상의 원소가 있을 때부터 비교 시작, 총 원소의 개수에서 1을 뺀 만큼 최대 비교
    - 마지막 남은 원소는 비교 없이 남은 자리에 들어감
- 합병의 시간 복잡도 $= O(m + n)$

총 비교 횟수

각각의 합병에 대해서 몇 번의 비교가 수행되었는지를 계산하여 이들을 모두 합한 수

층별 비교 횟수

각 층을 살펴보면 모든 숫자가 합병에 참여
합병은 입력 크기에 비례하므로 각 층에서 수행된 비교 횟수는 $O(n)$
- 2번 x 4, 4번 x 2, 8번 x 1

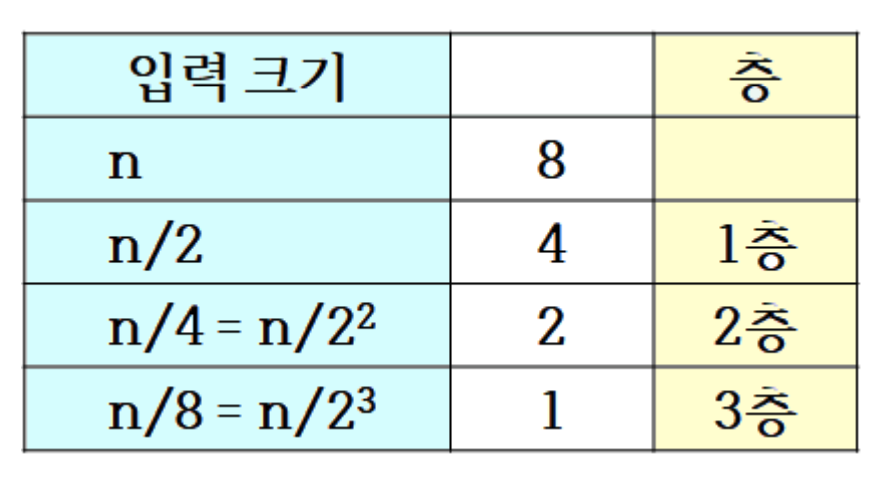
층수를 세어보면 8개의 숫자를 반으로, 반의 반으로, 반의 반의 반으로 나눈다. 이 과정을 통하여 세 층이 만들어진다. k번 1/2로 분할했으면 k개의 층이 생기는 것이고 k는 $2^k = n$ 으로부터 $log_2 n$ 임을 알 수 있다.

합병할 때 비교 연산을 수행하므로, 층별 비교 횟수 = 합병 시간 복잡도이다.

합병 정렬의 시간 복잡도

(층수) $\times O(n) = log_2 n \times O(n) = O(n log_2 n)$

3.1.3 Cons

대부분의 정렬 알고리즘들은 입력을 위한 메모리 공간과 O(1) 크기의 메모리 공간만을 사용해 정렬
- O(1) 크기의 메모리 공간: 입력 크기 n과 상관없는 크기의 공간
합병 정렬의 공간 복잡도: O(n)
- 입력을 위한 메모리 공간(입력 배열) 외에 추가로 입력과 같은 크기의 임시 배열이 별도로 필요하다.
- 2개의 정렬된 부분을 하나로 합병하기 위해, 합병된 결과를 저장할 곳이 필요하기 때문이다.

3.1.4 Application

합병 정렬은 외부 정렬의 기본
연결 리스트에 있는 데이터를 정렬할 때도 효율적
- 일반적인 인덱스 기반은 비효율적, 합병 정렬은 포인터만 이용해서 가능하므로 자료구조 제약이 없다.
Multi-core CPU와 Multi GPU의 등장으로 정렬 알고리즘을 병렬화

3.2 Quick sort

실제 수행 과정: 정복 후 분할
2개의 부분 문제로 분할
- 각 부분 문제의 크기가 일정하지 않은 형태의 분할 정복 알고리즘

pivot이라 일컫는 배열의 원소를 기준으로 피봇보다 작은 숫자들은 왼편으로, 피봇보다 큰 숫자들은 오른편에 위치하도록 분할하고, 피봇을 그 사이에 놓는다. 분할된 부분문제들에 대해서도 순환으로 정렬

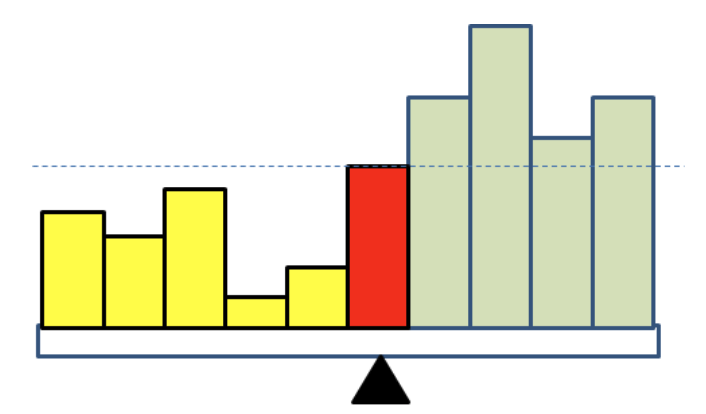
Pivot

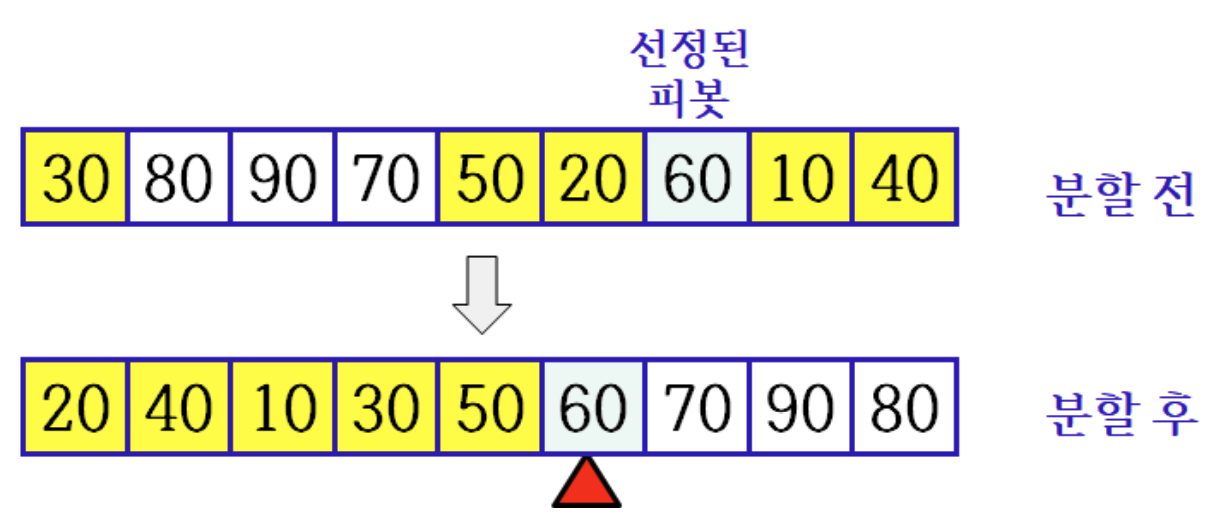
피봇은 분할된 왼편이나 오른편 부분에 포함되지 않는다.
- 피봇이 60이라면, 60은 [20 40 10 30 50]과 [70 80 90] 사이에 위치한다.

QuickSort(A, left, right)

Input: 배열 A[left] ~ A[right]
Output: 정렬된 배열 A[left] ~ A[right]

if (left < right){
$\,\,\,\,$ 피봇을 A[left]~A[right]에서 선택하고,
$\,\,\,\,$ 피봇을 A[left]와 자리를 바꾼 후, 피봇과 배열의 각 원소를 비교하여 피봇보다 작은 숫자들은
$\,\,\,\,$ A[left]~A[p-1]로 옮기고, 피봇보다 큰 숫자들은
$\,\,\,\,$ A[p+1]~A[right]로 옮기며, 피봇은 A[p]에 놓는다. // 정렬하는 과정 $O(n)$
$\,\,\,\,$ QuickSort(A, left, p-1) // 피봇보다 작은 그룹
$\,\,\,\,$ QuickSort(A, p+1, right) // 피봇보다 큰 그룹
}

3.2.1 Procedure

QuickSort(A, 0, 11)

8을 pivot으로 설정

Line2

피봇을 A[left]로 이동하고, 정렬하는 과정

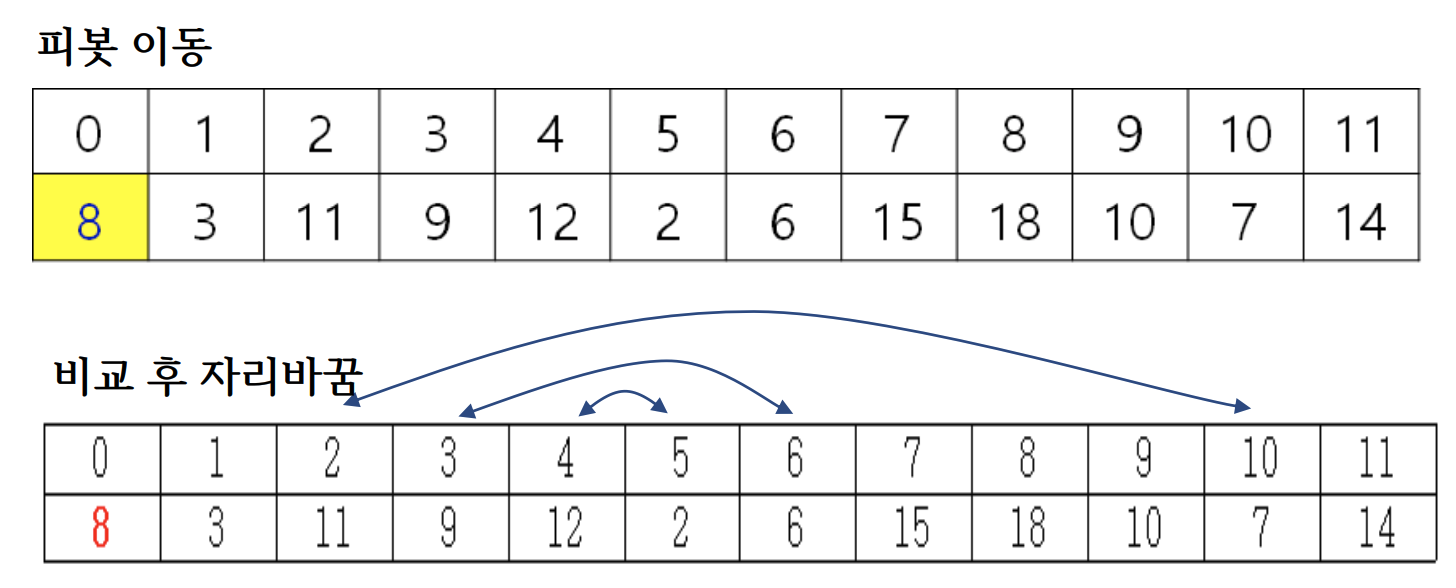
피봇 기준으로 왼쪽, 오른쪽 각각에서 인덱스를 가지고 비교하다가 어긋나면 멈추고, 두 위치의 값이 잘못된 순서라면 교환하여 정렬하고, 이 과정을 피봇 위치 주변에서 반복하는 방식이다.

피봇을 제자리로 이동

QuickSort(A, 0, 3): 순환 호출

Line2와 같은 과정

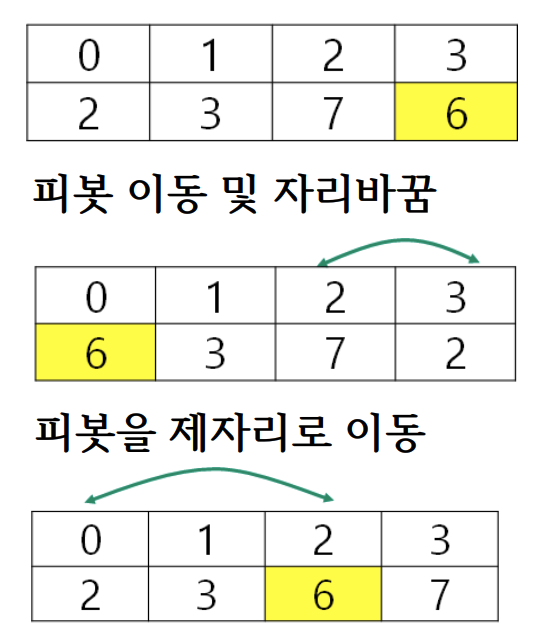
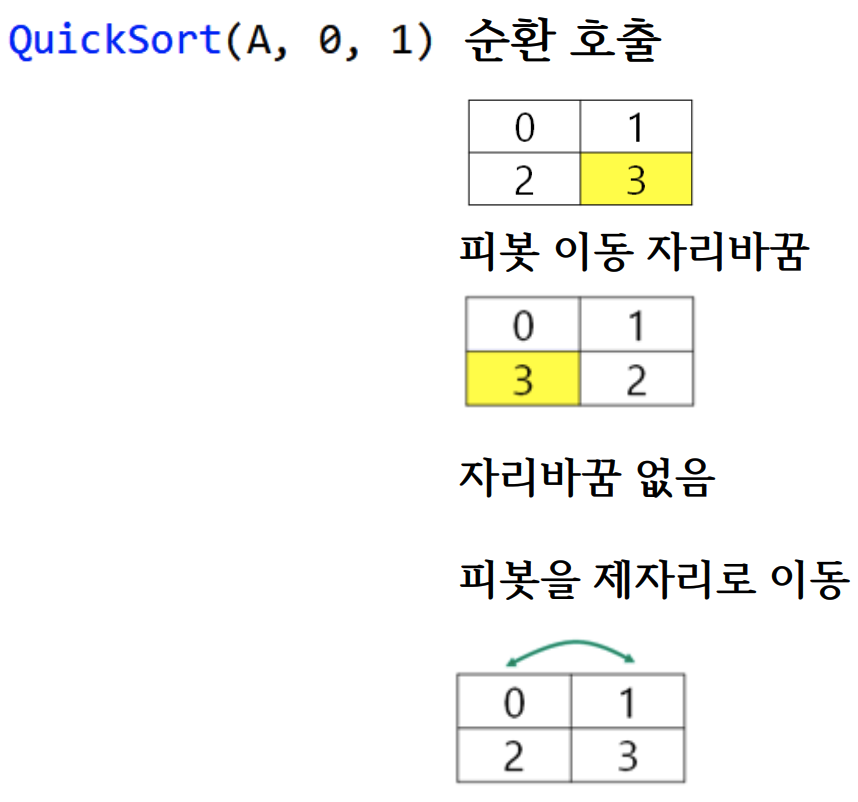
QuickSort(A, 0, 1), QuickSort(A, 3, 3): 순환 호출

QuickSort(A, 5, 11): 순환 호출

Line4

3.2.2. Time Complexity

퀵 정렬의 성능은 피봇 선택이 좌우한다.
- 피봇으로 가장 작은 숫자 또는 가장 큰 숫자가 선택되면, 한 부분으로 치우치는 분할 야기
  - 문제의 크기가 1씩 줄어들어 삽입 정렬이 된다.

Worst case

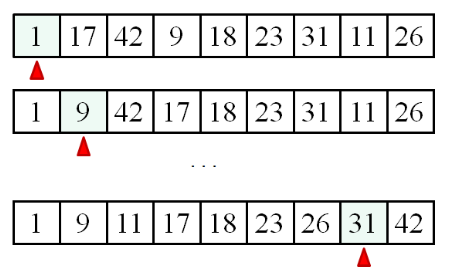
pivot = 1일 때, 8회
pivot = 9일 때, 7회
...
pivot = 31일 때, 1회 - 42와 1회 비교

최악의 경우 시간 복잡도는 $(n - 1) + (n - 2) + (n -3) + ... + 2 + 1 = n(n-1)/2 =$ $O(n^2)$

Best case

균등한 크기로 분할될 때

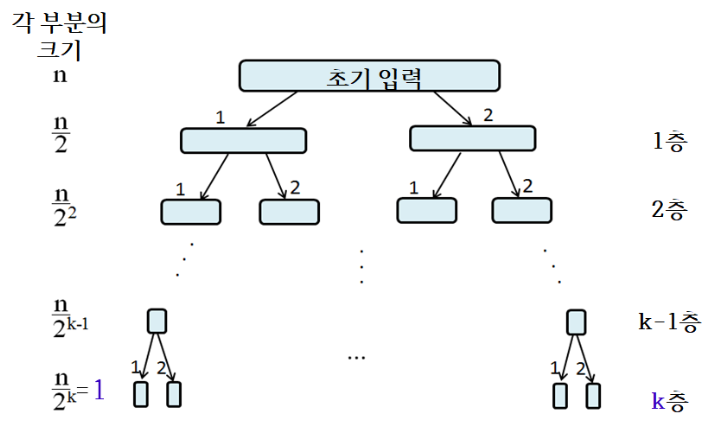
각 층에서는 각각의 원소가 각 부분의 피봇과 1회씩 비교된다.
- 따라서 비교 횟수 = $O(n)$
총 비교 횟수 = $O(n) \times$ (층수) $= O(n) \times logn$
$n/2^k = 1$ 일 때, $k=logn$ 이므로

최선의 경우 시간 복잡도는 $O(nlogn)$

Average case

pivot을 항상 랜덤하게 선택한다고 가정하면, 퀵 정렬의 평균 경우 시간 복잡도를 계산할 수 있다.

최선의 경우와 동일한 $O(nlogn)$ 이다.

3.2.3. Pivot Selection

1. Random

2. Median-of-Three

가장 왼쪽 숫자, 중간 숫자, 가장 오른쪽 숫자 중에서 중앙값으로 pivot을 정한다.
[31, 1, 26] 중에서 중앙값인 26을 pivot으로 사용

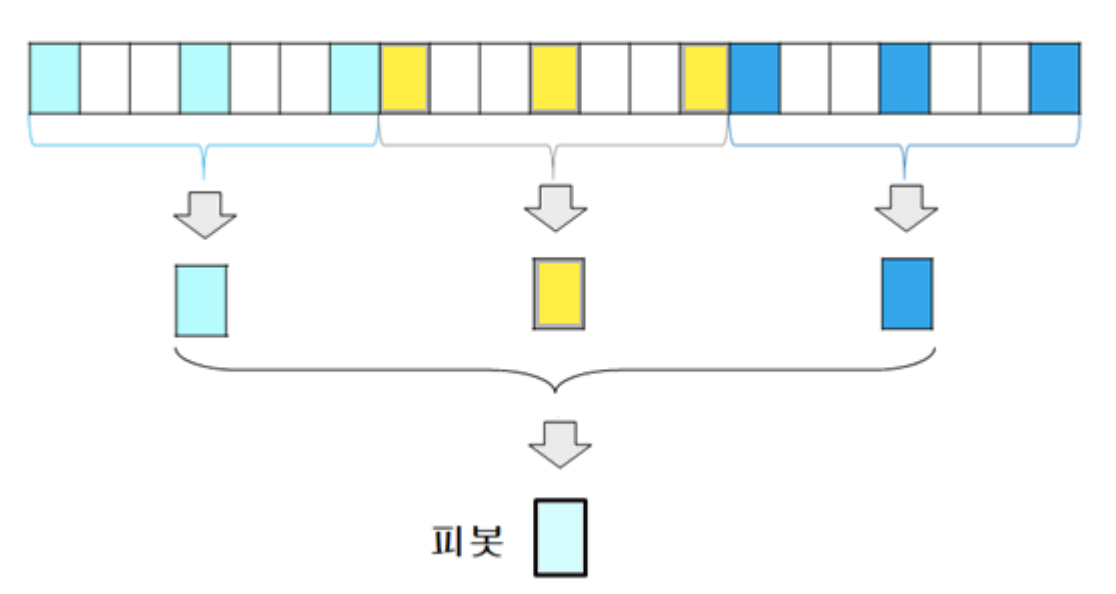
3. Median-of-Medians

3등분한 후 각 부분에서 가장 왼쪽 숫자, 중간 숫자, 가장 오른쪽 숫자 중에서 중앙값을 찾은 후, 세 중앙값들 중에서 중앙값을 피봇으로 정한다.

3.2.4 Performance improvement

입력의 크기가 매우 클 때, 퀵 정렬의 성능을 더 향상시키기 위해서, 삽입 정렬을 동시에 사용
- 입력의 크기가 작을 때에는 퀵 정렬이 삽입 정렬보다 빠르지만은 않다.
  - 퀵 정렬은 순환 호출로 수행되기 때문
부분 문제의 크기가 작아지면 (e.g., 대략 25 ~ 50), 더 이상의 분할(순환 호출)을 중단하고 삽입 정렬 사용

3.2.5 Application

커다란 크기의 입력에 대해서 가장 좋은 성능을 보이는 정렬 알고리즘
실질적으로 어느 정렬 알고리즘보다 좋은 성능을 보임
- 일반적으로
생물 정보 공학에서 특정 유전자를 효율적으로 찾는데 접미 배열과 함께 퀵 정렬 이용

dmswl

이전 포스트

2. What is Algorithm?

다음 포스트