3. Divide and conquer algorithm (2)

3.3 Selection

선택 문제는 n개의 숫자들(not 정렬) 중에서 k번째로 작은 숫자를 찾는 문제이다.

단순한 알고리즘

• 최소 숫자 숫자를 k번 찾는다. $O(n) \times k = O(kn)$
  • 단, 최소 숫자를 찾은 뒤에는 입력에서 최소 숫자 제거
• 숫자들을 정렬한 후, k번째 숫자를 찾는다.
  • 퀵 정렬 $O(nlong)$ + 순차 탐색 $O(n)$ = $O(nlogn)$

위 알고리즘들은 각각 최악의 경우 $O(kn)$과 $O(n logn)$의 수행 시간이 걸린다.

3.3.0 Idea

Binary search

• 정렬된 입력의 중간에 있는 숫자와 찾고자 하는 숫자를 비교함으로써, 입력을 1/2로 나눈 두 부분 중에서 한 부분만 검색

Selection

• 입력이 정렬되어 있지 않으므로, 입력 숫자들 중에서 (퀵 정렬과 같이) pivot을 선택하여 분할

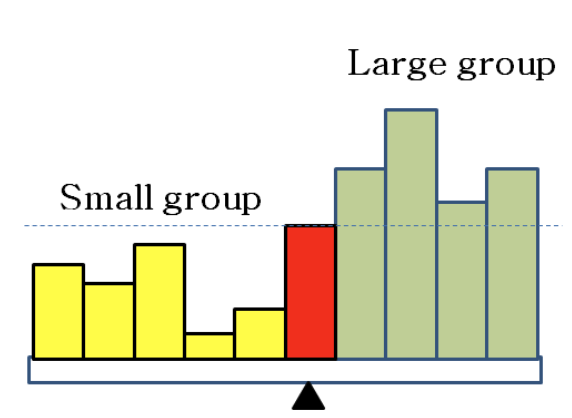
Small group < pivot < Large group

이렇게 분할했을 때 알아야 할 것은 각 그룹의 크기(숫자 갯수) 이다.
각 그룹의 크기를 알면 k번째 작은 숫자가 어느 그룹에 있는지 알 수 있고, 그 다음에는 그 그룹에서 몇 번째로 작은 숫자를 찾아야 하는지 알 수 있다.

• Small group에 k번째 작은 숫자가 속한 경우
  • k번째 작은 숫자를 Small group에서 찾는다.
• Large group에 k번째 작은 숫자가 있는 경우
  • k - | small group | - 1 번째로 작은 숫자를 Large group에서 찾아야 한다.
    • | small group |: small group에 있는 숫자 갯수, 1: pivot

Selection(A, left, right, k)

• Input: A[left]~A[right]와 k
• Output: A[left]~A[right]에서 k번째 작은 원소

1. pivot을 A[left]~A[right]에서 랜덤하게 선택하고, pivot과 A[left]의 자리를 바꾼 후,
   pivot과 배열의 각 원소를 비교하여 pivot보다 작은 숫자는 A[left]~A[p-1]로 옮기고,
   pivot보다 큰 숫자는 A[p+1]~A[right]로 옮기며, pivot은 A[p]에 둔다.
2. S = (p - 1) - left + 1 // S = small group size
3. if (K $\leq$ S) Selection(A, left, p-1, k) // Small group에서 찾기
4. else if (K = S + 1) return A[p] // pivot = k번째 작은 숫자
5. else Selection(A, p+1, right, k-S-1) // Large group에서 찾기

3.3.1 Procedure

k = 7

• 7번째로 작은 숫자 찾기

1. Selection(A, 0, 11, 7) 호출

2. Line2: Small group 크기 계산

S = (p - 1) - left + 1 = (4 - 1) - 0 + 1 = 4
k = 7로 large group에 속하므로 Line 5로 넘어간다.

3. Selection(A, 5, 11, 2) 호출

• k = 2, left = 5, right = 11
  • $k \leftarrow k - S - 1$
  • 7 - 4 - 1 = 2

4. Line2: Small group 크기 계산

• S = (p - 1) - left + 1 = (9 - 1) - 5 + 1 = 4

5. Selection(A, 5, 8, 2) 호출

위 과정에서 k = 7에서 k = 2가 되면서 k $\leq$ S 조건이 성립되어 small group에서 재귀호출을 한다. 인덱스 5부터 8까지의 구간에서 2번째로 작은 수를 찾는 문제가 된다.

• 원소 간 자리바꿈 없이 아래와 같이 된다.

6. Line2: Small group 크기 계산

• S = (p - 1) - left + 1 = (6 - 1) - 5 + 1 = 1

7. Line3~4

• Line3: if 조건 k $\leq$ S = (2 $\leq$ 1)은 false
• Line4: if 조건 (2 = S + 1) = (2 = 1 + 1) = (2 = 2)이 true이므로 최종적으로 A[6] = 10을 7번째 작은 수로 리턴

3.3.2 Consideration

• Selection 알고리즘은 분할 정복 알고리즘이기도 하지만 Random 알고리즘이기도 하다.
  • 선택 알고리즘의 Line1에서 pivot을 랜덤하게 정하기 때문이다.
• pivot이 입력을 너무 한쪽으로 치우치게 분할하면
  • = (small group과 large group 크기가 많이 다르면)
  • 알고리즘 수행 시간이 길어진다.
• 선택 알고리즘이 호출될 때마다 Line1에서 입력을 한쪽으로 치우치게 분할된 확률은? 1/2

3.3.3 Good/bad divide

• 분할된 두 그룹 중의 하나의 크기가 입력의 크기 3/4과 같거나 그보다 크게 분할하면 bad divide 라고 정의하자.
• good divide는 그 반대의 경우이다.

• e.g. 16개의 숫자

• good 분할이 되는 pivot을 선택할 확률과 bad 분할이 되는 pivot을 선택할 확률이 각각 1/2로 동일하다.

3.3.4 Time Complexity

• pivot을 random하게 정했을 때 good 분할이 될 확률이 1/2이므로 평균 2회 연속해서 random하게 pivot을 정하면 good 분할을 할 수 있다.
  • 1/2 $\rightarrow$ 1

매 2회 호출마다 good 분할이 되므로, good 분할만 연속하여 이루어졌을 때만의 시간 복잡도를 구하여, 그 값에 2를 곱하면 평균 시간 복잡도를 얻는다.

연속된 good 분할

Average case

• 입력 크기가 n에서부터 3/4배 연속적으로 감소되고, 크기가 1일 때는 더 이상 분할이 불가하다.
  $n + \frac{3}{4}n + \left(\frac{3}{4}\right)^2 n + \left(\frac{3}{4}\right)^3 n + \cdots + \left(\frac{3}{4}\right)^{i-1} n + \left(\frac{3}{4}\right)^i n$
  $= n[1 + \frac{3}{4} + \frac{3}{4}^2 + \frac{3}{4}^3 + ... + \frac{3}{4}^{i-1} + \frac{3}{4}^i] \leq 4n = O(n)$

• 평균 2회에 good 분할이 되므로 $2 \times O(n) = O(n)$

3.3.5 Selection vs. Binary search

Similarity

• Binary search는 분할 과정을 진행하면서 범위를 1/2씩 좁혀가며 찾고자하는 숫자 탐색
• Selection은 pivot으로 분할하여 범위를 좁혀감
  • 확실한 절반이 아니다.

Common Points

• 부분 문제들을 취합하는 과정이 별도로 필요 없다.
  • 분할 자체가 정복이다.

3.3.6 Application

• Selection은 데이터 분석을 위한 median을 찾는데 활용
  • 데이터 분석에서 평균보다 중앙값이 더 설득력 있는 데이터 분석 제공
  • e.g. 대부분의 데이터가 1이고, 오직 1개의 숫자가 매우 큰 noise이면 평균값은 왜곡된 분석이 된다.

3.4 Closest pair

2차원 평면상의 n개의 점이 입력으로 주어질 때, 거리가 가장 가까운 한 쌍의 점을 찾는 문제

Simple solution

• 모든 점에 대해 각각의 두 점 사이의 거리를 계산해 가장 가까운 쌍 찾기
• 비교해야 할 쌍의 갯수
  • $nC_2 = n(n-1)/2$
  • 한 쌍의 거리 계산은 $O(1)$
  • 시간 복잡도는 $O(n^2) \times O(1) = O(n^2)$

3.4.1 $O(n^2)$보다 효율적인 분할 정복: Closest pair

• n개의 점을 1/2로 분할해 각각의 부분 문제에서 최근접 점의 쌍을 찾고, 2개의 부분 해 중에서 짧은 거리를 가진 쌍을 일단 찾는다.

• 중간 영역에 있는 점들

• 10과 15 중에서 짧은 거리인 10 이내의 중간 영역 안에 있는 점들 중에 더 근접한 점의 쌍이 있는지 확인한다.

중간 영역에 있는 점들을 찾는 방법

• d = min{왼쪽 부분의 최근접 점의 쌍 사이의 거리, 오른쪽 부분의 최근접 점의 쌍 사이의 거리}
• 배열에는 점들이 x-좌표의 오름차순 정렬
• y-좌표 생략

• 중간 영역에 속한 점
  • 왼쪽 부분 문제의 가장 오른쪽 점의 x-좌표에서 d를 뺀 값과 오른쪽 부분 문제의 왼쪽 점의 x-좌표에서 d를 더한 값 사이의 x-좌표 값을 가진 점들
• d = 10이면, 25, 26, 28, 30, 37이 중간 영역이다.

ClosestPair(S)

• Input: x-좌표의 오름차순으로 정렬된 배열 S에 있는 i개의 점(x,y)
• Output: S에 있는 점들 중 최근접 점의 쌍의 거리

1. if (i $\leq$ 3) return (2 또는 3개의 점들 사이의 최근접 쌍)
2. 정렬된 S를 같은 크기의 $S_L$과 $S_R$로 분할한다. |S|가 홀수이면, $S_L$ = $S_R$ + 1이 되도록 분할
3. $CP_L$ = ClosestPair($S_L$)
4. $CP_R$ = ClosestPair($S_R$)
5. d = min{dist($CP_L$), dist($CP_R$)}일 때, 중간 영역에 속하는 점들 중에서 최근접 점의 쌍을 찾아서 이를 $CP_C$라고 하자.
6. return ($CP_L$, $CP_C$, $CP_R$ 중에서 거리가 가장 짧은 쌍)

dist()는 두 점 사이의 거리

3.4.2 Procedure

1. ClosestPair(S)로 호출 [1]

• Line1: S 점 > 3이므로 다음 line
• Line2: S를 $S_L$과 $S_R$로 분할

2. ClosestPair($S_L$)로 호출 [2]

3. ClosestPair($S_R$)로 호출

둘 다 점의 갯수가 3 이하

4. $CP_C$ 찾기

• [2]의 ClosestPair($S_L$) 호출 당시 line 3~4 수행, 이제 line 5를 수행한다. 즉 중간영역에서 $CP_C$를 찾는다.

제일 작은 dist($CP_C$) = 10을 선택한다.

5. [1]의 ClosestPair($S_R$)

• line4에서는 ClosestPair($S_R$) 호출 결과

6. Line5: $CP_C$ 찾기

• line 3~4에서 찾은 최근접 점의 쌍 사이의 거리인 dist($CP_L$)= 10, dist($CP_R$)= 15 중에 작은 값을 d라고 놓는다.

7. Line6: 최종 return

• dist($CP_L$)= 10, dist($CP_C$) = 5, dist($CP_R$)= 15 중에서 가장 거리가 짧은 쌍인 $CP_C$를 최근접 쌍의 점으로 return한다.

분할 정복 개념도

크기가 3 이하가 될 때까지 분할하고, 중간 영역은 따로 추가한다.

3.4.3 Time Complexity

$O(nlogn)$

• S에 n개의 점이 있으면 전처리 과정으로서 S의 점을 x-좌표로 정렬

Line1: $O(1)$

• 점의 수에 따라 3번(3개) or 1번(2개)의 거리 계산 필요

Line2: $O(1)$

• 정렬된 S를 $S_L$과 $S_R$로 분할, 정렬된 상태이므로 배열의 중간 인덱스만 분할

Line3

• $S_L$과 $S_R$에 대하여 각각 ClosestPair를 호출, 분할하며 호출되는 과정은 합병 정렬과 동일

Line5

• d = min{dist($CP_L$), dist($CP_R$)}일 때, 중간 영역에 속하는 점들 중 최근접 점 쌍을 찾는 과정
  1. y-좌표 기준 정렬: 중간 영역 점들 y-좌표 순으로 정렬 $O(nlogn)$
  2. 효율적 탐색: 아래에서 위로 각 점을 기준으로 거리가 d 이내인 주변 점들 사이 거리만 계산 $O(1)$
  • 주변 점들의 수가 $O(1)$개이기 때문이다.
  3. 거리 갱신: 계산된 거리 중 d보다 작은 값이 있으면 d 갱신

전체 분할은 x좌표를 기준으로 오름차순 분할, 중간 영역을 처리할 때는 경계선 근처 d 거리 이내의 점들만 추출한 후, 별도의 리스트를 모아 y좌표 기준 오름차순 정렬

Line6: $O(1)$

• 3개의 점의 쌍 중 가장 짧은 거리 return

Closest Pair 알고리즘의 분할 과정은 합병 정렬의 분할 과정과 동일하다.

• 그러나, Closest Pair는 해를 취합하여 올라가는 과정인 line 5~6에서 $O(nlogn)$ 시간이 필요하다.
• k층까지 분할된 후, 층별로 line5~6에서 수행되는 취합 과정을 보여준다.
  • 각 층의 수행 시간은 $O(nlogn)$
  • 여기에 층 수인 $logn$을 곱하면 $O(nlog^2 n)$

3.5.3 Application

• Computer graphics
• Computer vision
• GIS
• Molecular Modeling
• Air Traffic Control
• Marketing

3.5 Caution in divide and conquer

분할 정복이 부적절한 경우

• 입력이 분할될 때마다 부분 문제의 입력 크기의 합이 분할되기 전의 입력 크기보다 커지는 경우

n번째의 피보나치 수 구하기

• F(n) = F(n-1) + F(n-2)로 정의되므로 순환 호출을 사용하는 것이 자연스러워 보이나, 이 경우 입력은 1개이지만, 사실상 n의 값 자체가 입력의 크기
• 2개의 부분 문제인 F(n-1)과 F(n-2)의 입력 크기는 (n-1)+(n-2) = 2n-3이 되어서, 분할 후 입력 크기는 거의 2배로 증가한다.

F(6)을 구하기 위해 F(2)를 5번이나 중복하여 계산해야 하고, F(3)은 3번 계산된다. 위 경우 binary tree의 형태로 대략 $O(2^n)$이다.

FibNumber(n)

1. F[0] = 0
2. F[1] = 1
3. for i = 2 to n
4. $\,\,\,\,$ F[i] = F[i - 1] + F[i - 2]

피보나치 수 계산을 위한 시간 복잡도 $O(n)$의 알고리즘이다.

취합(정복) 과정

• 입력을 분할만 한다고 해서 효율적인 알고리즘이 아니다.
• 기하에 관련된 다수의 문제들이 효율적인 분할 정복 알고리즘으로 해결되는데, 이는 기하 문제들의 특성상 취합 과정이 문제 해결에 잘 부합되기 때문이다.

취합 과정에서 추가 cost가 많으면 쓸모가 없어진다.