[Paper Review] FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness

Abstract

• make attention algorithnms IOaware;accounting for reads and writes between levels of GPU memory
• FlashAttention
  • IO-aware exact attention algorithm
  • use tiling to reduce the number of memory reads/writes between GPU high bandwidth memory (HBM) and GPU on-chip SRAM
  • requires fewer HBM accesses than standard attention
  • is optimal for a range of SRAM sizes
• extend FlashAttention to block-sparse FlashAttention;faster than any existing approximate attention method
• trains Transformers faster than existing baselines
• enable longer context in Transformers
• entirely new capabilities: the first Transformers to achieve better-than-chance performance on the Path-X challenge

Introduction

• equipping Transformer models with longer context remains difficult, since the self-attention module at their heart has time and memory complexity quadratic in sequence length.
• whether making attention faster and more memory-efficient can help Transformer models with longer context
• Many approximate attention methods have aimed to reduce the compute and memory requirements of attention but did not display wall-clock speedup against standard attention
• One main reason is that they focus on FLOP reduction (which may not
  correlate with wall-clock speed) and tend to ignore overheads from memory access (IO)
• a missing principle is making attention algorithms IO-aware—that is, carefully accounting for reads and writes to different levels of fast and slow memory (e.g., between fast GPU on-chip SRAM and relatively slow GPU high bandwidth memory, or HBM)
  
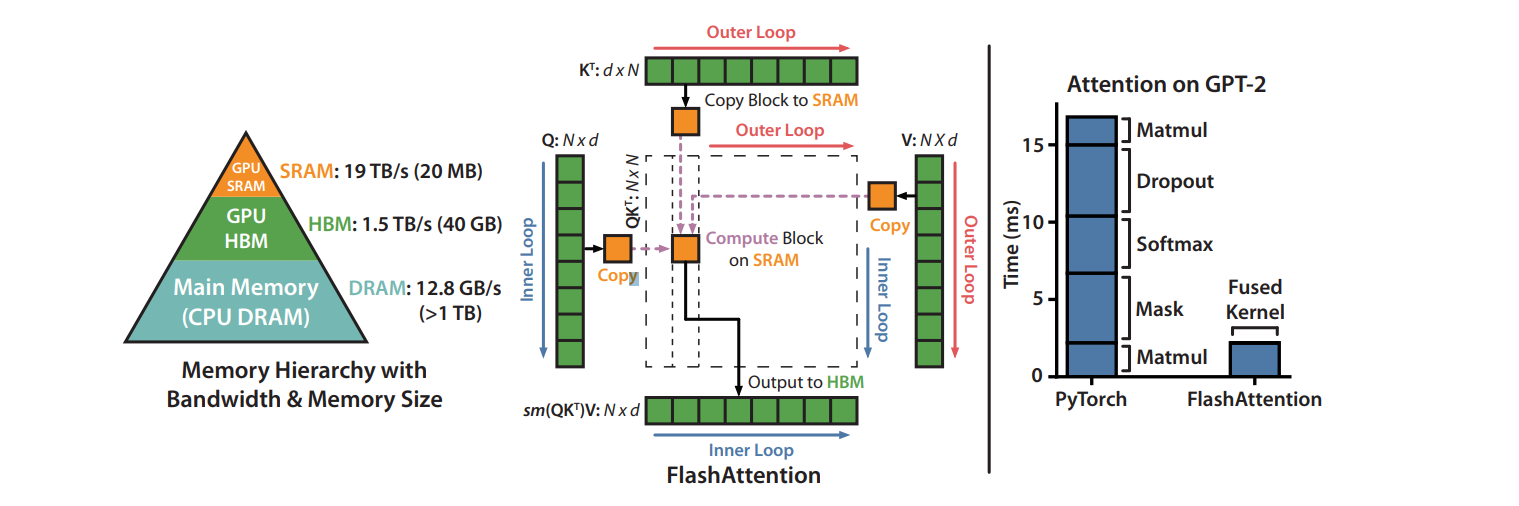
• most operations in Transformers are bottlenecked by memory accesses
• common Python interfaces to deep learning such as PyTorch and Tensorflow do not allow fine-grained control of memory access
• FlashAttention computes exact attention with far fewer memory accesses
• avoid reading and writing the attention matrix to and from HBM
  i. computing the softmax reduction without access to the whole input
  restructure the attention computation to split the input into blocks and make several passes over input blocks, thus incrementally performing the softmax reduction (also known as tiling)
  ii. not storing the large intermediate attention matrix for the backward pass
  store the softmax normalization factor from the forward pass to quickly recompute attention on-chip in the backward pass; faster than the standard approach of reading the intermediate attention matrix from HBM
• implement FlashAttention in CUDA to achieve fine-grained control over memory access and fuse all the attention operations into one GPU kernel
• Even with the increased FLOPs due to recomputation, our algorithm both runs faster and uses less memory, thanks to the massively reduced amount of HBM access
• block-sparse FlashAttention even faster than even FlashAttention
• FlashAttention speeds up model training and improves model quality by modeling longer context

Background

• kernel fusion
  • the most common approach to accelerate memory-bound operations
  • if there are multiple operations applied to the same input, the input can be loaded once from HBM, instead of multiple times for each operation
• However, in the context of model training, the intermediate values still need to be written to HBM to save for the backward pass, reducing the effectiveness of naive kernel fusion

FlashAttention: Algorithm, Analysis, and Extensions

An Efficient Attention Algorithm With Tiling and Recomputation

• two established techniques (tiling, recomputation)
• split the inputs $Q, K, V$ into blocks
• load them from slow HBM to fast SRAM
• compute the attention output with respect to those blocks
• scaling the output of each block by the right normalization factor before adding them up
• tiling
  • softmax of vector $𝑥 ∈ R^B$ is computed as:
    
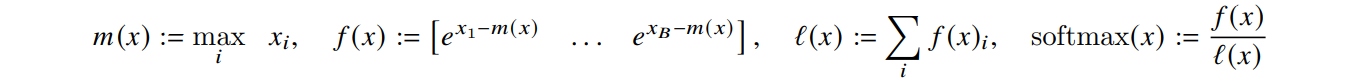
  • For vectors $x^{(1)}, x^{(2)} ∈ R^B$, we can decompose the softmax of the concatenated $x = [x^{(1)}, x^{(2)}] ∈ R^{2B}$ as:
    
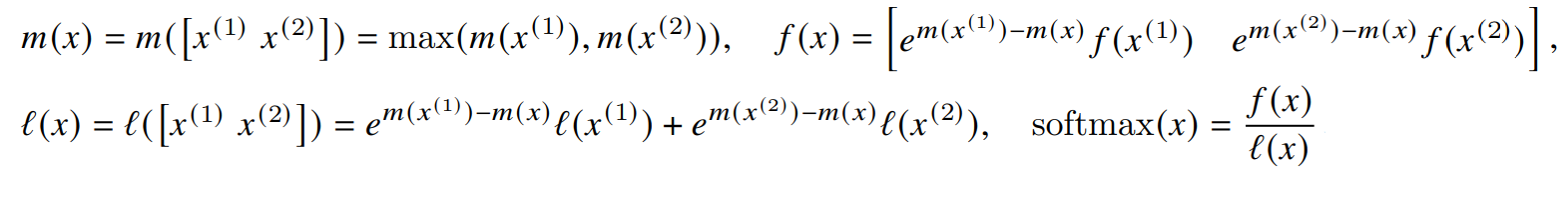
  • can compute softmax one block at a time
  • split the inputs $Q, K, V$ into blocks (Algorithm 1 line 3), compute the softmax values along with extra statistics (Algorithm 1 line 10), and combine the results (Algorithm 1 line 12)
• recomputation
  • backward pass typically requires the matrices $S, P ∈ R^{N × N}$ to compute the gradients with respect to $Q, K, V$
  • However, by storing the output $O$ and the softmax normalization statistics $(𝑚, ℓ)$, we can recompute the attention matrix $S$ and $P$ easily in the backward pass from blocks of $Q, K, V$ in SRAM (selective gradient checkpointing)
  • While gradient checkpointing has been suggested to reduce the maximum amount of memory required, have to trade speed for memory.
  • even with more FLOPs, faster due to reduced HBM accesses
• Implementation details: Kernel fusion
  • Tiling enables us to implement our algorithm in one CUDA kernel, loading input from HBM, performing all the computation steps, then write the result back to HBM
  • This avoids repeatedly reading and writing of inputs and outputs from and to HBM