2-1. Loss Function

본 글은 K-MOOC의 인공지능 수학 고급(Advanced Mathematics for AI) 강의를 듣고 요약한 글입니다.

Problem

광고 예산에 따른 TV의 판매량을 다음과 같은 그래프로 나타내었다.

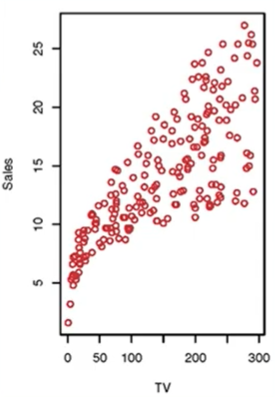
이 때, 새로운 광고 예산에 대한 TV의 판매량을 예측하는 문제이다.

Data

다음과 같이 변수를 정의하자.

• $X$: TV 광고 예산 (input variable, features)
• $Y$: 판매량 (output variable, response variable)
• $(x^{(i)}, y^{(i)})$: $i$번째 학습 데이터

이를 통해 우리는 이 그래프를 행렬로 표현할 수 있다.

$X$	$Y$
230.1	22.1
44.5	10.4
17.2	9.3
151.5	18.5
$\vdots$	$\vdots$

Linear Regression

우리는 이를 위해 선형회귀분석을 사용할 것이다.

모델을 다음과 같이 정의하자. $Y \approx \beta_0 + \beta_1X$

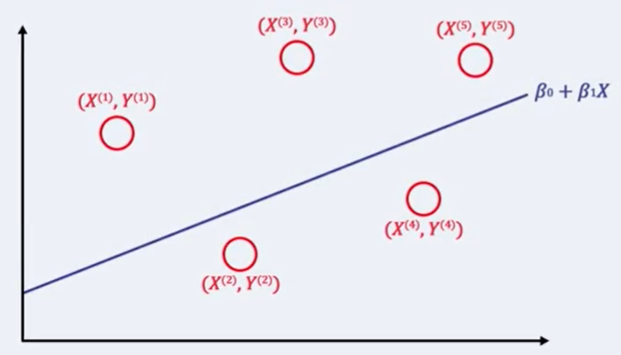
이 때 우리는 최적의 $\beta_0, \beta_1$을 찾는 문제로 문제를 변형할 수 있다.

즉, 같은 $x^{(i)}$에 대해서, $\hat{y}^{(i)}$ 와 $y^{(i)}$ 의 차이가 최소가 되는 $\beta_0, \beta_1$를 찾으면 된다.

Euclidean distance를 이용하여 차이를 계산한다고 가정할 때, 모든 차이를 다음과 같이 계산할 수 있을 것이다.

이 함수를 바로 Loss function이라고 정의한다.

그럼 문제가 다음과 같이 바뀐다.

이를 최적화하는 알고리즘에 대해서는 다음 강의에서 다룬다.