2-2. Optimization using GD

본 글은 K-MOOC의 인공지능 수학 고급(Advanced Mathematics for AI) 강의를 듣고 요약한 글입니다.

Optimization

• 특정 함수를 주어진 조건에 맞춰 최대화 또는 최소화하는 것
• 최대화 하는 경우 - Objective Function
• 최소화 하는 경우 - Loss Function
• 주어진 조건: Feasible region 또는 Constraint region

Gradient Descent

목표: loss function을 최소화하는 것.

현재 위치가 $(\tilde{\beta}_0, \tilde{\beta}_1)$라고 하자.

Loss function의 함숫값을 $L(\tilde{\beta}_0, \tilde{\beta}_1)$이라고 할 때, Loss function의 함숫값을 작게 만드는 방향은 다음과 같다.

이 방향을 통해 계속 이동하다보면 함숫값을 감소시킬 수 있을 것이다.

더 이상 작아지지 않는다면 그 곳은 극소점이 될 것이다.

산의 정상을 찾아보자.

위의 설명이 너무 어렵다면 구름이 가득한 산에서 지도 없이 정상을 찾는 과정과 비슷하다고 볼 수 있다.

우리는 현재 지점의 높이와 어느 방향으로 가야 높이가 증가하는 지 알 수 있다.

이때, 계속 몇 걸음씩 높이가 증가하는 방향으로 발걸음을 옮기다가 더 이상 높이의 변화가 없다면 산의 정상에 도착할 수 있을 것이다.

이러한 방식으로 최소점을 찾아나가는 방법이 Gradient Descent 방법이다.

Algorithm

• 초기값 $\tilde{\beta}_0$과 $\tilde{\beta}_1$을 랜덤하게 정한다.
• $\tilde{\beta}_0$과 $\tilde{\beta}_1$의 변화가 없을 때까지 아래 연산을 반복한다.

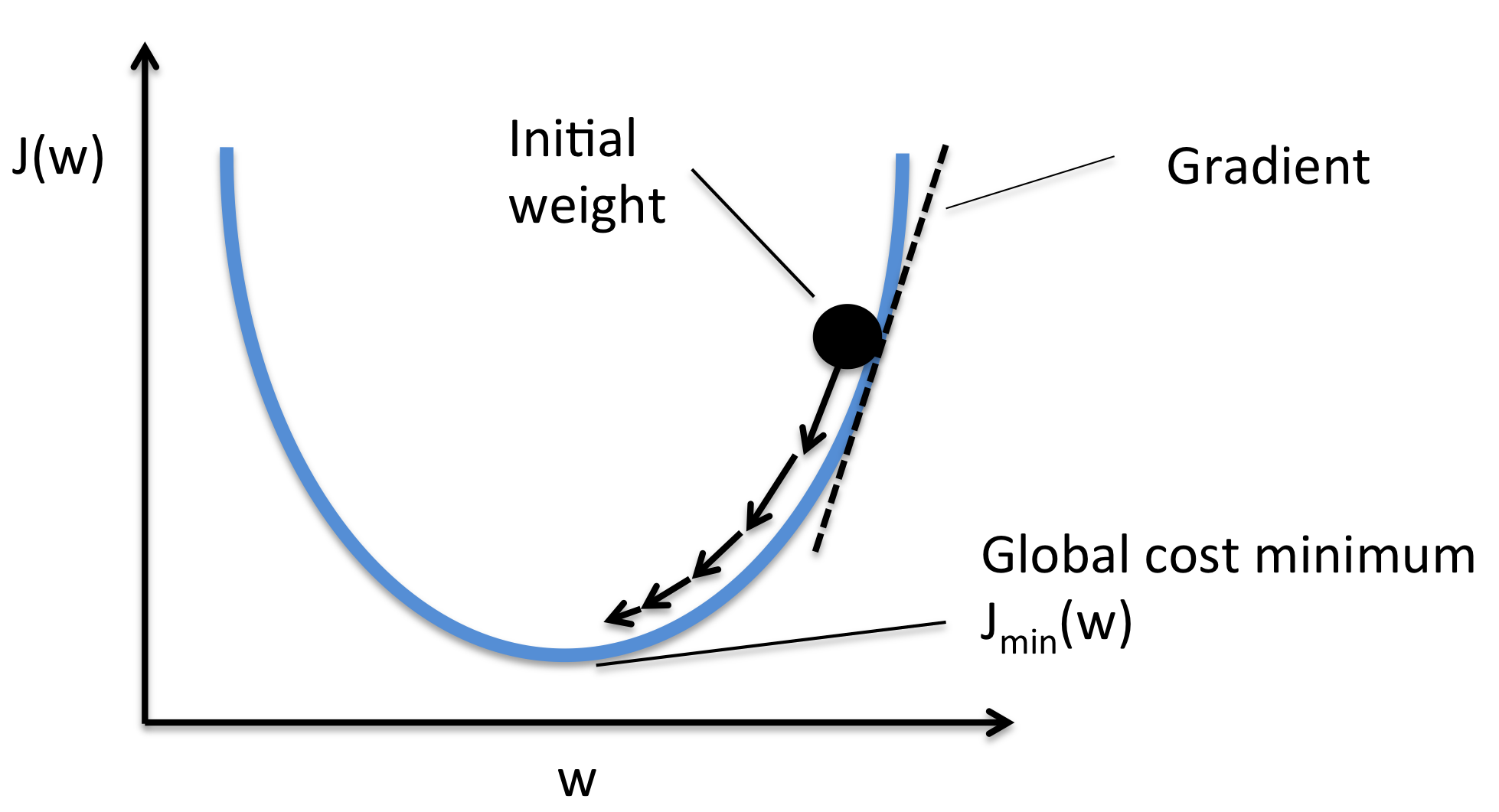
이 그림이 해당 알고리즘의 대략적인 도식이라고 본다면 이해하기 수월할 것이다.