2-3. Stochastic Gradient Descent

본 글은 K-MOOC의 인공지능 수학 고급(Advanced Mathematics for AI) 강의를 듣고 요약한 글입니다.

Linear Regression

이제 2-2, Optimization using GD에서 공부한 Gradient Descent를 2-1. Loss Function에서 다뤘던 Linear Regression에 적용해 보자.

우선은 식이 아래와 같을 것이다.

$\frac ∂ {∂x}(f+g) = \frac ∂ {∂x}f + \frac ∂ {∂x}g$ 이기 때문에 위 식을 아래와 같이 변형할 수 있다.

Stochastic Gradient Descent

위와 같은 식 덕분에 한번에 모든 데이터에 대한 Gradient descent를 계산하지 않고, $L$의 일부분에 대해서 미분을 하고 업데이트를 하고, 이를 반복하여 연산량을 줄일 수 있다.

전체 data들 사이에서 일부 data를 고른 다음에, 이 데이터들에 대해서만 경사하강법을 적용하는 방법이다.

이런 방법을 Mini-batch Gradient Descent라고 한다.

그리고 여기에서 이 batch의 크기가 1인, 즉 딱 한 데이터만 골라서 경사하강법을 적용하는 방법이 바로 Stochastic Gradient Descent이다.

다음 그림을 보면 좀 더 이해가 빠를 것이다.

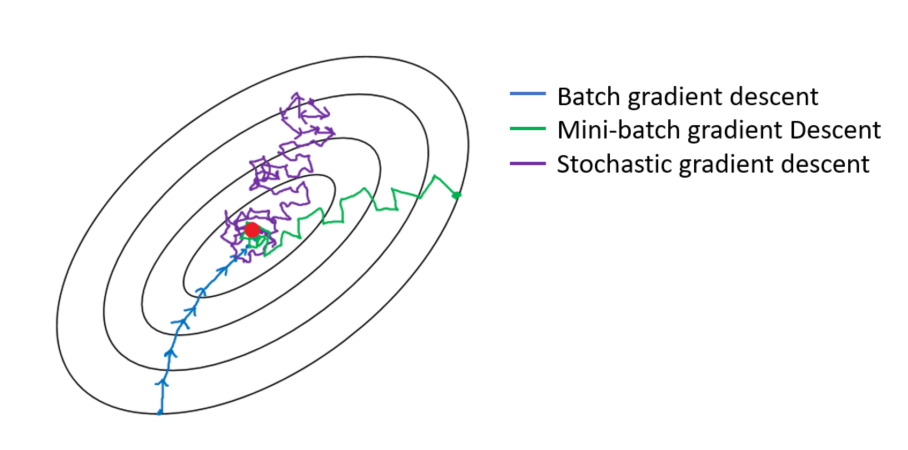
즉 정리하면 다음과 같다.

Gradient Descent는 각 스텝이 정확하지만 굉장히 느리고,
Stochastic Gradient Descent는 조금 헤메지만 빠르게 목적지를 찾아간다.