📦 Design and Timing Guarantee for Non-Preemptive Gang Scheduling

Introduction

• Non-Preemptive Gang Scheduling (이하 NPG)는 다음과 같은 새로운 형태의 Priority Inversion이 발생합니다.

• 이를 고려하여, 본 논문에서는 NPG 프레임워크 NPG*를 제안하여 이 새로운 형태의 Priority Inversion을 허용할지 말지를 결정할 수 있도록 합니다.
• 그리고 그 효과를 입증하기 위해 FP에 적용하여 NPG*-FP에 대해 다음 질문을 해결합니다.
  • 각 태스크에 대한 허용 옵션이 주어졌을 때, NPG*-FP의 Schedulability Test는 어떻게 개발할 수 있는가?
  • 이 Schedulability Test를 통해 target task set을 스케쥴 가능하게 하는 옵션을 어떻게 할당할 것인가?

System Model

• 본 논문에서는 fixed-priority scheduling을 사용합니다.
• $\tau^\text{HP}(\tau_k)$, $\tau^\text{LP}(\tau_k)$는 각각 $\tau_k$보다 높은 우선순위와 낮은 우선순위 태스크 집합을 의미합니다.
• 시간 간격인 $L$은 연속적이지 않을 수 있습니다. 즉, 다음과 같이 정의될 수 있습니다.
  $L' = [-2, 2) \cup [6,10)$

Scheduling Framework Design for NPG

먼저 NPG의 성질에 대해 관찰합니다.

PR 1 (Non-Preemptive)
낮은 우선순위의 작업 $J_i$는 높은 우선순위의 작업 $J_k$의 릴리스 시간 전에 실행을 시작하면 $J_k$의 실행을 막을 수 있습니다.

PR 2 (Different parallelism)

• $τ_i$에 의해 호출된 낮은 우선순위 작업($J_i$)과 $τ_k$에 의해 호출된 높은 우선순위 작업($J_k$)이 $t$ 이전에 릴리스되었지만 $t$ 이전에 실행을 시작하지 않는다고 가정합니다.
• $t$에서 $m_i \le m' < m_k$를 만족하는 $m'$개의 사용 가능한 프로세서가 있는 경우, $J_k$는 실행할 수 없지만 $J_i$는 실행을 시작할 수 있습니다.

PR 2는 PG에서는 문제가 되지 않았지만, NPG에서는 $J_k$의 완료시간을 미루게 됩니다.

그리고 이게 새로운 형태의 Priority Inversion을 발생시킵니다.

하지만 이러한 inversion을 허용하지 않는 것이 schedulability를 향상시키는 것은 아닙니다.

Example 1
4개의 태스크, 8개의 프로세서가 있다고 가정합시다.

• $\tau_1$: $T_1 = 25$, $C_1 = 4$, $D_1 = 25$, $m_1 = 2$
• $\tau_2$: $T_2 = 25$, $C_2 = 4$, $D_2 = 6\;or\;8$, $m_2 = 6$
• $\tau_3$: $T_3 = 25$, $C_3 = 4$, $D_3 = 4$, $m_3 = 3$
• $\tau_4$: $T_4 = 25$, $C_4 = 4$, $D_4 = 10\;or\;8$, $m_4 = 3$

$\tau_3$만 $-2$에 릴리즈되고, 나머지 태스크는 $0$에 릴리즈됩니다.

따라서 우리는 이러한 상황에서 inversion을 허용할 수 있는지 여부를 결정할 수 있는 이진 옵션 $\phi_k$를 제안합니다.

• $\phi_k = \text{T}$인 경우: $τ_k$ 작업보다 우선순위가 낮은 작업의 실행을 시작할 수 있습니다 (이는 기존 NPG의 메커니즘입니다).
• $\phi_k = \text{F}$인 경우: $τ_k$ 작업보다 우선순위가 낮은 작업의 실행을 시작할 수 없습니다.

Algorithm 1: NPG* Framework
작업의 선택은 릴리즈나 완료 시점에 결정됩니다.

for (ready queue에 있는 모든 작업에 대해 우선순위에 대해 내림차순으로): 
    if (사용 가능한 프로세서 수가 0): 
        return
    elif (m_k 보다 크거나 같은 프로세서가 있을 경우):
        J_k 실행
    elif phi_k == F: # 기존 NPG와 유일한 차이 
        return

• 그리고 작업이 모종의 이유로 ready 상태이지만 실행되지 못하고 있다면 이를 $pending$이라고 부릅니다.

Schedulability Analysis for NPG*-FP

Schedulability Test는 다음과 같이 개발합니다.

1. 런타임에만 드러나는 일부 값에 의존하는 각 작업의 Schedulability condition을 개발합니다.
2. 이러한 각 값의 오프라인 upper bound를 개별적으로 도출하여 첫번째 Schedulability test를 개발합니다.
3. 각 값의 upper bound를 좀 더 엄격하게 설정하는 방법을 개발하여 NPG*-FP의 Schedulability Test를 향상시킵니다.

A. Development of Each Job's Schedulability Condition

• $J_k$의 release time을 $r_k$라 할 때, $(D_k-C_k)$ 길이의 $\Delta_k = [r_k, r_k + D_k - C_k)$ 구간에 집중합니다.
• 만약 $\Delta_k$ 안에서 $J_k$가 pending 상태인 시간이 $(D_k - C_k)$보다 엄격하게 작다면, $J_k$는 non-preemptive하기 때문에 반드시 deadline을 맞출 수 있습니다.

이 시간을 표현하기 위해 다음과 같은 notation을 정의합니다.

• $\tau^\text{HPF}(\tau_k)$: $\tau_k$보다 높은 우선순위를 갖고, $\phi_h$가 F인 태스크 집합 $\{\tau_h \in \tau\} = \{\tau_h \in \tau^\text{HP}(\tau_k) | \phi_h = \text{F}\}$
• $L^\text{P}_k(\Delta)$: $\tau_k$가 pending 상태인 시간 간격
• $L^\text{PH}_k(\Delta)$: $\tau_k$가 pending 상태이고, pending 상태인 $\tau_h \in \tau^\text{HPF}(\tau_k)$가 존재하는 시간 간격. 즉:
  $L^\text{PH}_k(\Delta) = L^\text{P}_k(\Delta) \cap \bigcup_{\tau_h \in \tau^\text{HPF}(\tau_k)}L^\text{P}_h(\Delta)$
• $L^\text{PN}_k(\Delta)$ (이하 $L_k(\Delta)$): $\tau_k$가 pending 상태이고, pending 상태인 $\tau_h \in \tau^\text{HPF}(\tau_k)$가 존재하지 않는 시간 간격. 즉:
  $L^\text{PN}_k(\Delta) = L^\text{P}_k(\Delta) \setminus L^\text{PH}_k(\Delta)$

Example 2
4개의 태스크, 8개의 프로세서가 있다고 가정합시다.

• $\tau_1$: $T_1 = 25$, $C_1 = 4$, $D_1 = 25$, $m_1 = 2$
• $\tau_2$: $T_2 = 25$, $C_2 = 4$, $D_2 = 25$, $m_2 = 6$
• $\tau_3$: $T_3 = 25$, $C_3 = 4$, $D_3 = 25$, $m_3 = 3$
• $\tau_4$: $T_4 = 25$, $C_4 = 4$, $D_4 = 25$, $m_4 = 3$

$\tau_3$만 $-2$에 릴리즈되고, 나머지 태스크는 $0$에 릴리즈됩니다.
$\tau_1$이 가장 높은 우선순위, $\tau_4$가 가장 낮은 우선순위를 갖습니다. $\phi_2=F$

$\tau_4$는 $[0, 2) = L^\text{PH}_4(\Delta_4)$ 구간에서는 프로세서가 충분함에도, $\phi_2=F$이기 때문에 실행할 수 없습니다.
그 이후는 프로세서가 부족하므로 실행할 수 없습니다.

• 기존의 간섭 기반 프레임워크 에서 $τ_k$ 작업의 스케줄링 가능성은 다른 작업에서 사용하지 않는 프로세서 수가 관심 작업의 실행에 충분하지 않은 기간의 상한을 계산하여 판단합니다.
• 그러나 NPG*-FP에서는 프로세서 수가 충분하더라도 pending 상태일 수 있습니다.
• 이는 $L^\text{PH}_k(\Delta_k)$때문에 발생하므로, 우리는 $L^\text{PH}_k(\Delta_k)$를 $L_h(\Delta_k)$의 크기로 표현해야 합니다.

Lemma 1

$|L_k^{\text{PH}}(\Delta_k)| \leq \sum_{\tau_h \in \tau^{\text{HPF}}(\tau_k)} |L_h(\Delta_k)|. \tag{1}$

Proof
$L_k^{\text{PH}}(\Delta_k) \subseteq \bigcup_{\tau_h \in \tau^{\text{HPF}}(\tau_k)} L_h(\Delta_k)$를 증명하면 됩니다.

• 정의에 의해 $L^\text{PH}_k(\Delta_k) = L^\text{P}_k(\Delta_k) \cap \bigcup_{\tau_h \in \tau^\text{HPF}(\tau_k)}L^\text{P}_h(\Delta_k)$
• 따라서, $L_k^{\text{PH}}(\Delta_k) \subseteq \bigcup_{\tau_h \in \tau^{\text{HPF}}(\tau_k)} L^P_h(\Delta_k)$이고, 우리는 $\bigcup_{\tau_h \in \tau^{\text{HPF}}(\tau_k)} L^P_h(\Delta_k)=\bigcup_{\tau_h \in \tau^\text{HPF}(\tau_k)}L^\text{P}_h(\Delta_k)$를 보이면 됩니다.

(수학적 귀납법)

• (Base case) $\tau_{h_1}$이 가장 높은 우선순위를 갖게 되므로, $L^\text{PH}_{h_1}(\Delta_k)=\emptyset$. 따라서 $L^\text{P}_{h_1}(\Delta_k) = L_{h_1}(\Delta_k)$입니다.

• (Inductive case) $n-1$에 대해 성립한다고 가정합니다.
  $\begin{aligned} & \bigcup_{1 \le x \le n} L^P_{h_x}(\Delta_k)\\ = & \bigcup_{1 \le x \le n-1} L^P_{h_x}(\Delta_k) \cup L^P_{h_n}(\Delta_k) \\ = & \bigcup_{1 \le x \le n-1} L^P_{h_x}(\Delta_k) \cup L^{PH}_{h_n}(\Delta_k) \cup L_{h_n}(\Delta_k) && \text{(by the definition of } L_{h_n}^{P} (\Delta_k) ) \\ = & \bigcup_{1 \le x \le n-1} L_{h_x}^P (\Delta_k) \cup \{L_{h_n}^P (\Delta_k) \cap \bigcup_{1 \le x \le n-1} L_{h_x}^P (\Delta_k) \} \cup L_{h_n}(\Delta_k) && \text{(by the definition of } L_{h_n}^{PH} (\Delta_k) ) \\ = & \bigcup_{1 \le x \le n-1} L_{h_x}^P (\Delta_k) \cup L_{h_n}(\Delta_k) && \text{(by } L \cup \{L' \cap L\} = L ) \\ = & \bigcup_{1 \le x \le n-1} L_{h_x}(\Delta_k) \cup L_{h_n}(\Delta_k) && \text{(by the supposition)} \\ = & \bigcup_{1 \le x \le n} L_{h_x}(\Delta_k) \end{aligned}$
  따라서 수학적 귀납법에 의해 성립합니다.

Lemma 2
만약 다음 부등식을 만족한다면 $r_k$에 릴리즈된 $\tau_k$의 작업은 deadline을 맞출 수 있습니다.

$|L_k(\Delta_k)| + \sum_{\tau_h \in \tau^{\text{HPF}}(\tau_k)} |L_h(\Delta_k)| < D_k - C_k \tag{2}$

Proof

• 정의에 의해 $L^{PH}_{k}(\Delta_k) \cup L_{k}(\Delta_k) = L^{P}_{k}(\Delta_k)$이고, $L^{PH}_{k}(\Delta_k) \cap L_{k}(\Delta_k) = \emptyset$입니다.
• 즉 $|L^{PH}_{k}(\Delta_k)| + |L_{k}(\Delta_k)| = |L^{P}_{k}(\Delta_k)|$입니다.
• Eq.(1)을 이 방정식에 대입하면, $|L^{P}_{k}(\Delta_k)| \le$ Eq (2)의 LHS가 성립합니다.
• 따라서 Eq (2)가 성립하면 $|L^{P}_{k}(\Delta_k)| < D_k - C_k$가 성립합니다.
• $L^{P}_{k}(\Delta_k)$의 정의와 $\Delta_k$의 길이에 따라 $|L^{P}_{k}(\Delta_k)| < D_k - C_k$는 $J_k$가 $r_k+D_k-C_k$ 전에 실행을 시작함을 의미합니다.
• non-preemptive이므로 $J_k$는 deadline을 맞출 수 있습니다.

$\tau_i$가 $|L_k(\Delta_k)|$와 $|L_h(\Delta_k)|$에 기여하는 양을 표현하기 위해 다음 notation을 정의합니다.

• $L_{k \leftarrow i}(\Delta)$: $L_k(\Delta)$ 중 $\tau_i$가 실행중인 시간 간격

Lemma 3

$\left|L_{k}\left(\Delta_{k}\right)\right| \leq \sum_{\tau_{i} \in \tau \setminus\left\{\tau_{k}\right\}} \frac{\left|L_{k \leftarrow i}\left(\Delta_{k}\right)\right| \cdot \min \left(m_{i}, m - m_{k} + 1\right)}{m - m_{k} + 1} \tag{3}$

그리고 $\Delta_k$에서 $J_k$의 실행이 없다면, 다음이 성립합니니다.

$|L_h(\Delta_k)| \leq \sum_{\tau_i \in \tau \setminus \{\tau_h, \tau_k\}} \frac{|L_{h \leftarrow i}(\Delta_k)| \cdot \min(m_i, m - m_h + 1)}{m - m_h + 1} \tag{4}$

Proof
(귀류법) Eq(3)이 성립하지 않을 때 가정의 모순을 증명합니다.

• $L$ 시간동안 $m_k$의 프로세서를 실행할 때 amount of execution을 $|L|\cdot m_k$로 정의합니다.
• $L_{k}\left(\Delta_{k}\right)$의 정의에 의해 적어도 $(m-m_k+1)$개의 프로세서가 $L_{k}\left(\Delta_{k}\right)$의 어떤 시간에서든 실행되고 있어야 합니다.
• 여기에서 임의의 $(m-m_k+1)$개 프로세서를 선택해 counted processors라고 한다면, counted processors에서 $L_{k}\left(\Delta_{k}\right)$의 실행량은 정확히 $|L_{k}\left(\Delta_{k}\right)|\cdot (m-m_k+1)$입니다.

• 반면, $L_{k}\left(\Delta_{k}\right)$에서의 $\tau_i$의 실행량의 upper bound는 $|L_{k \leftarrow i}\left(\Delta_{k}\right)|\cdot \min(m_i, m-m_k+1)$입니다.
• 따라서 $\tau_k$를 제외한 모든 작업의 실행량은 $\sum_{\tau_{i} \in \tau \setminus\left\{\tau_{k}\right\}} \left|L_{k \leftarrow i}\left(\Delta_{k}\right)\right| \cdot \min \left(m_{i}, m - m_{k} + 1\right)$ 이하이고, 모순이 발생합니다.
• Eq(4)도 $\Delta_k$에서 $J_k$의 실행이 없음을 가정하므로, RHS에서 $\tau_k$와 관련된 항을 제거해 증명할 수 있습니다.

이 보조정리들을 합해 다음 정리를 증명할 수 있습니다.

Theorem 1
다음 부등식이 성립한다면, $\tau_k$는 $r_k+D_k-C_k$ 이전에 실행되고, 따라서 deadline을 맞출 수 있습니다.

$\begin{aligned} \sum_{\tau_h \in \tau^{HPF}(\tau_k)} \left( \sum_{\tau_i \in \tau \setminus \{\tau_h, \tau_k\}} \frac{|L_{h \leftarrow i}(\Delta_k)| \cdot \min(m_i, m - m_h + 1)}{m - m_h + 1} \right) \\+ \sum_{\tau_i \in \tau \setminus \{\tau_k\}} \frac{|L_{k \leftarrow i}(\Delta_k)| \cdot \min(m_i, m - m_k + 1)}{m - m_k + 1} \\ < D_k - C_k \end{aligned} \tag{5}$

다만 여기에서 $|L_{h \leftarrow i}(\Delta_k)|$와 $|L_{k \leftarrow i}(\Delta_k)|$는 런타임 전에 알 수 없으므로, offline test를 개발하기 위해 upper bound를 도출해야 합니다.

B. Development of Schedulability Analysis for NPG*-FP

$\phi_k=T$인 경우와 $\phi_k=F$인 경우를 나누어 upper bound를 도출합니다.
$\phi_k=T$인 경우는 $\tau_i$의 관계를 다음 세 개로 나누어 생각할 수 있습니다.

1. $\tau_i \in \tau^{\text{HP}}(\tau_k)$
2. $\tau_i \in \tau^{\text{LP}}(\tau_k) | m_i \ge m_k$
3. $\tau_i \in \tau^{\text{LP}}(\tau_k) | m_i < m_k$

$\tau_i \in \tau^{\text{HP}}(\tau_k)$인 경우:

• $W_i(\ell)$을 연속된 길이 $\ell$의 시간 동안 $\tau_i$가 최대 실행될 수 있는 시간이라고 할 때,
• $|L_{k \leftarrow i}(\Delta_k)|$의 upper bound를 $W_i(D_k-C_k)$로 할 수 있습니다.
• 아래 그림에 따라 최대 실행은 $\tau_i$의 첫번째 작업이 $\ell$의 최대한 늦게 실행되고, 그 이후는 최대한 빨리 실행될때 발생합니다.
  

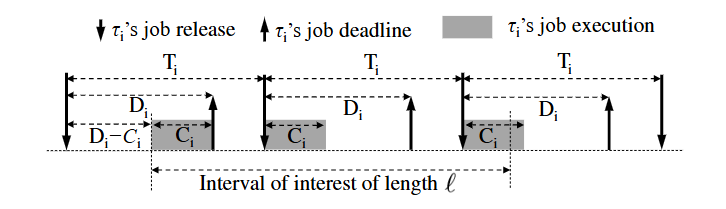
• 따라서, $N_i(\ell)$을 $\left\lfloor\frac{\ell + D_i - C_i}{T_i}\right\rfloor$라 정의할 때 다음과 같이 계산됩니다.

$\tau_i \in \tau^{\text{LP}}(\tau_k) | m_i \ge m_k$인 경우:

• 우리는 $|L_{k \leftarrow i}(\Delta_k)|$의 upper bound를 $min(D_k-C_k, C_i)$로 할 수 있습니다.
• $m_i$가 $m_k$보다 크거나 같고, $\tau_i$의 우선순위가 $\tau_k$보다 낮으므로, PR2의 상황은 발생할 수 없습니다.
• 따라서, 오직 PR1에 의해 $\tau_i$가 실행될 수 있고, 이는 $r_k$ 전에 $\tau_i$의 실행이 시작되어야 합니다.
• 즉 $min(D_k-C_k, C_i)$로 upper bound가 정해집니다.

$\tau_i \in \tau^{\text{LP}}(\tau_k) | m_i < m_k$인 경우:

• 이때는 PR2의 상황이 발생할 수 있으므로 prioirty inversion이 발생할 수 있고, 따라서 $W_i(D_k-C_k)$가 upper bound가 됩니다.

정리하면 $\phi_k=T$인 경우는 다음과 같이 upper bound를 도출할 수 있습니다.

한편 $\phi_k=T$인 경우는 $\tau_i$의 관계를 다음 두 개로 나누어 생각할 수 있습니다.

1. $\tau_i \in \tau^{\text{HP}}(\tau_k)$
2. $\tau_i \in \tau^{\text{LP}}(\tau_k)$

$\tau_i \in \tau^{\text{HP}}(\tau_k)$인 경우:
똑같이 $W_i(D_k-C_k)$가 upper bound가 됩니다.

$\tau_i \in \tau^{\text{LP}}(\tau_k)$인 경우:
반드시 PR1만 발생할 수 있으므로, $min(D_k-C_k, C_i)$가 upper bound가 됩니다.

정리하면 $\phi_k=F$인 경우는 다음과 같이 upper bound를 도출할 수 있습니다.

Lemma 4
$\tau$가 NPG*-FP에서 스케쥴될 때, 다음 부등식이 성립힌다.

$|L_{k \leftarrow i}(\Delta_k)| \leq E_{k \leftarrow i}, \tag{9}$

다음 단계는 $|L_{h \leftarrow i}(\Delta_k)|$의 upper bound를 도출하는 것입니다.

$L_{h \leftarrow i}(\Delta_k)$에 포함되는 임의의 구간은 다음을 만족합니다.
1. $\tau_i$의 작업이 실행중이고
2. $\tau_h$의 작업이 pending 상태이고
3. $\tau_g \in \tau^\text{HPF}(\tau_h)$의 작업중 pending 상태인 작업이 없습니다.

2번과 3번이 복잡하기 때문에 우선 1번 조건만 다룹니다.

$W_i(\ell)$이 $\ell$의 길이동안 $\tau_i$가 최대 실행될 수 있는 시간이므로, $|L_{h \leftarrow i}(\Delta_k)| \leq W_i(D_k-C_k)$가 성립합니다.

$|L_{h \leftarrow i}(\Delta_k)|$의 upper bound $E_{h \leftarrow i}(\tau_k)$를 다음과 같이 정의합시다.

Lemma 5

$|L_{h \leftarrow i}(\Delta_k)| \leq E_{h \leftarrow i}(\tau_k), \tag{11}$

이제 Lemma 4와 Lemma 5를 합쳐서 Theorem 2를 만들 수 있습니다.

Theorem 2
task set $\tau$가 NPG*-FP에서 스케쥴 가능할 때, 다음 부등식이 성립합니다.

$\begin{aligned} \sum_{\tau_h \in \tau^{HPF}(\tau_k)} \left( \sum_{\tau_i \in \tau \setminus \{\tau_h, \tau_k\}} \frac{E_{h \leftarrow i}(\tau_k) \cdot \min(m_i, m - m_h + 1)}{m - m_h + 1} \right)\\ + \sum_{\tau_i \in \tau \setminus \{\tau_k\}} \frac{E_{k \leftarrow i} \cdot \min(m_i, m - m_k + 1)}{m - m_k + 1} < D_k - C_k \end{aligned} \tag{12}$

Proof
$\tau_k$의 작업 $J_k$의 Deadline miss를 가정합시다.
Eq (5)는 Eq (12)로 upper bound되고, Eq(5)가 성립하면 Theorem 1에 의해 deadline miss가 발생하지 않으므로 모순됩니다.

이 방법은 NPG*-FP 뿐만 아니라, 기존 NPG-FP에도 사용할 수 있습니다. ($\phi_k=T$인 경우)

시간복잡도는 $\phi_i=F$를 만족하는 태스크 수를 $n'$, 전체 태스크 수를 $n$이라고 할 떄 $O(n' \cdot n^2)$입니다.

C. Improvement of Schedulability Analysis for NPG*-FP

Example 3
4개의 태스크, 8개의 프로세서가 있다고 가정합시다.

• $\tau_1$: $T_1 = 25$, $C_1 = 4$, $D_1 = 25$, $m_1 = 2$
• $\tau_2$: $T_2 = 25$, $C_2 = 4$, $D_2 = 25$, $m_2 = 6$
• $\tau_3$: $T_3 = 25$, $C_3 = 4$, $D_3 = 25$, $m_3 = 3$
• $\tau_4$: $T_4 = 25$, $C_4 = 4$, $D_4 = 25$, $m_4 = 3$

$\phi_2=\phi_3=F$라고 하면 $\tau_1$은 $E_{4 \leftarrow 1}$, $E_{3 \leftarrow 1}(\tau_4)$, $E_{2 \leftarrow 1}(\tau_4)$에서 Eq(12)의 LHS에 기여하게 됩니다.
그러나 $\tau_1$은 $D_4-C_4$동안 최대 $W_1(D_4-C_4) = 8$만큼밖에 실행할 수 없고 이는 Eq(12)의 LHS에 반영되어 있지 않습니다.

Lemma 6
모든 $\tau_{h}, \tau_{h_2} \in \tau^\text{HPF}(\tau_k)$에 대해 다음 두 부등식이 성립합니다.

$L_k(\Delta_k) \cap L_h(\Delta_k) = \emptyset \tag{13}$

$L_{h_2}(\Delta_k) \cap L_h(\Delta_k) = \emptyset \tag{14}$

Proof

• Eq (13)이 성립하지 않는다고 가정하면 $L_k(\Delta_k) \cap L_h(\Delta_k) = L$이 존재합니다.
• $L_h(\Delta_k$의 정의에 의해 $L$에서 pending 중인 $\tau_h$의 작업이 존재합니다.
• $L_k(\Delta_k)$의 정의에 의해 $L$에서 pending 중인 $\tau_h$의 작업이 존재하지 않습니다.
• 따라서 모순이 발생하여 Eq(13)은 성립합니다.
• Eq (14)도 일반성을 잃지 않고 $\tau_h$의 우선순위가 $\tau_{h_2}보다 높다고 가정하면 똑같이 증명할 수 있습니다.

즉 우리는 모든 $L_k(\Delta_k)$와 $L_h(\Delta_k)$가 서로소임을 알 수 있습니다.

또한 정의에 의해 $L_{k \leftarrow i}(\Delta_k)$는 $L_k(\Delta_k)$의 부분집합이므로, Theorem 1의 모든 $L_{k \leftarrow i}(\Delta_k)$와 $L_{h \leftarrow i}(\Delta_k)$도 서로소입니다.

따라서 이러한 서로소 성질을 이용하여 Theorem 1의 $\tau_i$와 관련된 interval의 upper bound를 설정할 수 있습니다.

Lemma 7
$r_k$가 $J_k$의 release time이고, $\Delta_k=[r_k, r_k+D_k-C_k)$ 사이에 $J_k$가 실행되지 않는다면 $\tau_k$를 제외한 모든 $\tau_i$에 대해 다음이 성립합니다.

$|L_{k \leftarrow i}(\Delta_k)| + \sum_{\tau_h \in \tau^{\text{HPF}}(\tau_k)} |L_{h \leftarrow i}(\Delta_k)| \leq E_{k \leftarrow i} \tag{15}$

Proof
우선 $E_{k \leftarrow i}$를 $|L_{k \leftarrow i}(\Delta_k)|$의 upper bound로 유도하는 과정에서 생각해봅시다.

• $L_{k \leftarrow i}(\Delta_k)$는 $\tau_i$가 실행죄고, $\tau_k$의 작업이 pending 상태인 구간입니다.
• 따라서 $E_{k \leftarrow i}$는 $\Delta_k$ 안에서 $\tau_i$의 실행시간에 대한 upper bound입니다.

만약 Eq (15)가 성립하지 않는다고 가정하면,

• Lemma 6에 의해 모든 $L_{k \leftarrow i}(\Delta_k)$와 $L_{h \leftarrow i}(\Delta_k)$도 서로소이므로
• 모든 $L_{h \leftarrow i}(\Delta_k)$의 길이의 합과 $L_{k \leftarrow i}(\Delta_k)$의 길이의 합의 upper bound는 $\Delta_k$ 안에서 $\tau_i$의 실행시간이 됩니다.
• 이는 위 증명과 모순되므로, Eq (15)가 성립합니다.

이제 Lemma 7과 Theorem 1을 합쳐 Schedulability Test를 도출할 수 있습니다.

Lemma 8
Eq(17)을 만족하는 모든 $E'_{k \leftarrow i} \ge 0$과 $E'_{h \leftarrow i} \ge 0$의 조합에 대해 Eq(16)이 모든 $\tau_k \in \tau$에 대해 성립할 때 $\tau$가 NPG*-FP로 스케쥴 가능하다.

$\begin{aligned} \sum_{\tau_h \in \tau^{\text{HPF}}(\tau_k)} \left( \sum_{\tau_i \in \tau \setminus \{\tau_h, \tau_k\}} \frac{E'_{h \leftarrow i}(\tau_k) \cdot \min(m_i, m - m_h + 1)}{m - m_h + 1} \right) \\+ \sum_{\tau_i \in \tau \setminus \{\tau_k\}} \frac{E'_{k \leftarrow i} \cdot \min(m_i, m - m_k + 1)}{m - m_k + 1} < D_k - C_k \end{aligned} \tag{16}$

$E'_{k \leftarrow i} + \sum_{\tau_h \in \tau^{\text{HPF}}(\tau_k)} E'_{h \leftarrow i}(\tau_k) \leq E_{k \leftarrow i} \tag{17}$

Eq(16)의 LHS는 항상 Eq(12)의 LHS보다 작거나 같으므로, Lemma 8은 Theorem 2보다 향상된 버전입니다.

• 그러나 Lemma 8이 많은 assignment에 대한 계산을 수반하기 때문에, Eq(16)의 LHS를 최대화하는 $E'_{k \leftarrow i} = E^*_{k \leftarrow i}$와 $\{E'_{h \leftarrow i}(\tau_k) = E^*_{h \leftarrow i}(\tau_k)\}$를 찾아야 합니다.

Algorithm 2는 $E^*_{k \leftarrow i}$와 $E^*_{h \leftarrow i}(\tau_k)$를 찾는 방법을 보여줍니다.

Lemma 9
Algorithm 2로 찾은 $E^*_{k \leftarrow i}$와 $E^*_{h \leftarrow i}(\tau_k)$는 Eq (18)을 최대화 합니다. (Eq (16)의 LHS에서 $\tau_i$를 포함하는 항의 합)

$\sum_{\tau_h \in \tau^{\text{HPF}}(\tau_k)} \frac{E'_{h \leftarrow i}(\tau_k) \cdot \min(m_i, m - m_h + 1)}{m - m_h + 1} + \frac{E'_{k \leftarrow i} \cdot \min(m_i, m - m_k + 1)}{m - m_k + 1} \tag{18}$

Proof

어떤 다른 $E'_{k \leftarrow i} = E''_{k \leftarrow i}$와 $\{E'_{h \leftarrow i}(\tau_k) = E''_{h \leftarrow i}(\tau_k)\}$가 존재하여 Eq(18)이 $E^*$보다 더 크다고 가정해봅시다.
$\tau_x = \tau_k$ (4번째 줄)에 대해 증명합니다. else는 비슷하게 증명할 수 있습니다.

• 먼저 $E''_{k \leftarrow i} > E^*_{k \leftarrow i}$인 경우, 4번째 줄에 의해 $E''_{k \leftarrow i} > E_{k \leftarrow i}$가 되고, Eq(17)에 위반되므로 모순입니다.
• $E''_{k \leftarrow i} < E^*_{k \leftarrow i}$인 경우, Eq(17)의 LHS가 RHS와 같은 경우에 대해 살펴봅시다. (다르다면 임의로 $E''_{k \leftarrow i}$나 $E''_{h \leftarrow i}(\tau_k)$를 증가시켜도 Eq(17)이 성립하는 선에서 Eq(18)을 증가시킬 수 있습니다.)
• 이때 $E''_{k \leftarrow i}$를 $(E^*_{k \leftarrow i}-E''_{k \leftarrow i})$만큼 증가시키고, 어떤 $E''_{h \leftarrow i}(\tau_k)$를 $(E^*_{k \leftarrow i}-E''_{k \leftarrow i})$만큼 감소시킬 수 있습니다.
• 그러면 $(E_{k \leftarrow i}^* - E_{k \leftarrow i}^{\prime\prime}) \cdot (\frac{min(m_i, m - m_k + 1)}{m - m_k + 1} - \frac{min(m_i, m - m_h + 1)}{m - m_h + 1}) \ge 0$ 이므로, Eq(18)을 더 증가시킬 수 있습니니다.
• 그러나 이제 $E''$는 $E^*$와 같아졌으므로, 이는 가정에 모순됩디다.

Theorem 3
다음 부등식이 성립한다면 $\tau$가 NPG*-FP로 스케쥴 가능합니다.

$\begin{aligned} \sum_{\tau_h \in \tau^{HPF}(\tau_k)} \left( \sum_{\tau_i \in \tau \setminus \{\tau_h, \tau_k\}} \frac{E_{h \leftarrow i}^*(\tau_k) \cdot \min(m_i, m - m_h + 1)}{m - m_h + 1} \right) \\+ \sum_{\tau_i \in \tau \setminus \{\tau_k\}} \frac{E_{k \leftarrow i}^* \cdot \min(m_i, m - m_k + 1)}{m - m_k + 1} < D_k - C_k \end{aligned}\tag{19}$

Optimal Assignment of $\{\phi_j\}$ for NPG*-FP

$\phi_h$의 변화가 더 높은 우선순위의 작업, 낮은 우선순위의 작업, 그리고 본인에게 미치는 영향을 다음과 같이 정리할 수 있습니다.

Lemma 10

S1. $\tau_h \in \tau^{\text{LP}}(\tau_k)$인 경우

• Eq(12)의 LHS는 $\phi_h$가 T일때와 F일때가 같습니다.

S2. $\tau_h \in \tau^{\text{HP}}(\tau_k)$인 경우

• Eq(12)의 LHS는 $\phi_h$가 T일때가 F일때보다 작거나 같습니다.

S3. $\tau_h = \tau_k$인 경우

• Eq(12)의 LHS는 $\phi_h$가 T일때가 F일때보다 크거나 같습니다.

이는 Eq(12)를 Eq(19)로 대체해도 성립합니다.

Proof
우선 Eq(12)의 LHS에서 영향을 받는 부분은 $E_{k \leftarrow i}$와 $E_{h \leftarrow i}(\tau_k)$, 그리고 $\tau^\text{HPF}(\tau_k)$입니다.

• $E_{k \leftarrow i}$에 집중하자면, $\phi_k=T$일 때 Eq (7), $\phi_k=F$일 때 Eq (8)로 $E_{k \leftarrow i}$가 계산됩니다.
• 이 둘이 달라지는 부분은 오직 $\tau_i \in \tau^{\text{LP}}(\tau_k) | m_i < m_k$인 경우입니다.
• $W_i(D_k-C_k)$가 $\min(D_k-C_k, C_i)$보다 크거나 같으므로, $\phi_k$가 F일 때 더 작거나 같은 값을 갖습니다. 따라서 S3이 성립합니다.

$\phi_k$와 다르게, $E_{k \leftarrow i}$와 $E_{h \leftarrow i}$는 $\phi_i$와 $\phi_h$에 따라 달라지지 않습니다. 따라서 S1이 성립합니다.

• 반면 만약 더 높은 우선순위의 작업의 $\phi_h$가 F로 바뀐다면, 낮은 우선순위 작업인 $\phi_k$는 $\tau^\text{HPF}(\tau_k)$가 늘어나므로, 더 커지게 됩니다. 따라서 S2가 성립합니다.

다음으로 Eq(19)에 대해 증명합니다.

• 우리는 Lemma 8의 모든 상한이 S1-S3과 일치함을 보여야 합니다.
• Lemma 8의 Eq (17)에 있는 상한은 $E_{k \leftarrow i}$뿐이며, Schedulability에 미치는 영향은 이미 증명되었기에, Eq(19)에 대해서도 성립합니다

이 Lemma 10을 이용해서 Algorithm 3을 만들 수 있습니다.

Theorem 4
Algorithm 3이 unschedulable을 리턴한다면, $\tau$를 스케쥴가능하게 만드는 Theorem 3에 대한 $\phi$의 조합은 존재하지 않는다.

Proof

Algorithm 3이 unschedulable을 리턴했지만 Theorem 3을 만족시키는 $\phi$의 조합이 존재한다고 가정합시다.

• 이 조합을 $\{\phi'_j\}_{\tau_j \in \tau}$라고 할 때, 가정에 의해 4번째 줄에서 Eq(19)가 Algorithm 3에 의해 할당된 모든 $\tau_h \in \tau^\text{HP}(\tau_k)$ 하에서 $\phi_k$가 T이던 F이던 성립하지 않음을 의미합니다.
• 이 할당을 $\{\phi^*_h\}_{\tau_h \in \tau^\text{HP}(\tau_k)}$라고 정의합시다.
• 이때 가장 높은 우선순위부터 낮은 우선순위까지 $\{\phi^*_h\} \neq \{\phi'_h\}$인 $\tau_h$를 조사합니다.
  1. 만약 그런 $\tau_h$가 없다면 $\phi' = \phi^*$ 이므로 모순됩니다.
  2. 만약 $\phi_h^*=F$와 $\phi_h'=T$를 만족하는 $\tau_h$가 있다면 이는 Algorithm 3의 동작과 모순됩니다. 낮은 우선순위에 대한 할당은 S1에 의해 Schedulability에 영향을 주지 않기 때문입니다.
  3. 만약 $\phi_h^*=T$와 $\phi_h'=F$를 만족하는 $\tau_h$가 있다면 이는 $\phi_h=F$가 S2에서 설명한 바와 같이 Eq(19)의 좌변을 감소시키지 않기 때문에 $\phi_h'$가 스케쥴 가능하다면 $\phi_h^*$도 스케쥴 가능해야 합니다. 따라서 모순입니다.

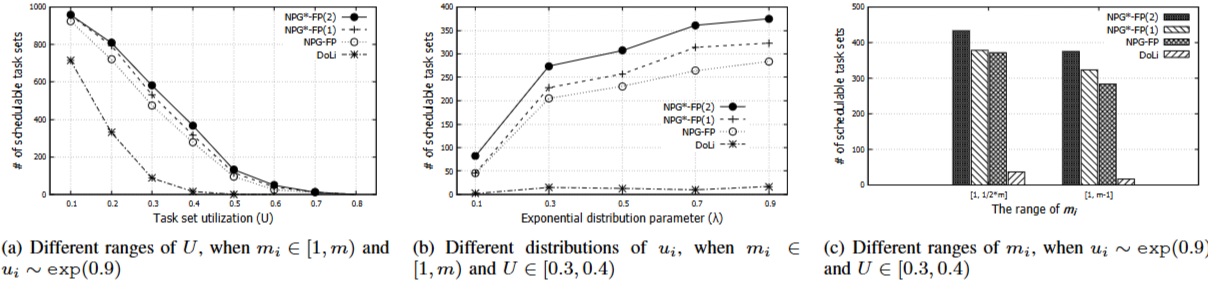
Evaluation

• DoLi: 이미 존재하는 NPG-EDF에 대한 schedulability test입니다.
• NPG-FP: Theorem 2를 NPG-FP에 적용한 테스트입니다.
• NPG-FP(1), (2): Theorem 2, 3을 Algorithm 3으로 구한 $\{\phi_j\}$ 하에에 NPG-FP에 적용한 테스트입니다.