📦 Strict Partitioning for Sporadic Rigid Gang Tasks

Introduction

• 병렬작업은 보통 Configuration 시간이 오래 걸리는 하드웨어에 탑재된다.
• Global Gang Scheduling은 마이그레이션 비용이 너무 크다.
• Partitioned Gang Scheduling은 각 모델에 대한 가중치를 내부 메모리에 정적으로 캐싱하여 메모리 할당의 비용을 줄인다.

Contribution

• Rigid Gang Scheduling을 위한 새로운 Strict Partitioning 전략을 제안한다.
• Rigid Gang Tasks를 나누기 위한 First-Fit Decreasing Volume (FFDV) heuristic을 제안한다.
• Strict Partitioning의 두 가지의 변형 SP-U와 SP-G를 제안한다.
  • SP-U는 Utilization bound를 증명한다.
  • SP-G는 FFDV가 더 나은 성능을 갖도록 향상시킨다.
• 제안된 전략과 알고리즘을 SOTA Preemptive / Non-Preemptive Gang Scheduling과 비교한다.
  • Edge TPU에서의 case study도 진행한다.

Strict Partitioning for Rigid Gang Tasks

Task and Platform Model

• $M$개의 동일한 프로세서로 구성된 멀티프로세서 플랫폼 $\Pi$
• $\tau_i \in \tau$, $\tau_i = (C_i, T_i, D_i, m_i)$
• $J_i$: $\tau_i$의 job, $r_i$: arrival time of $J_i$
• sequential utilization : $u_i = \frac{C_i}{T_i}$
• utilization: $U_i = m_i \cdot u_i$
• Task set utilization: $U = \sum_{i=1}^{n} U_i$
• $\overline{m}$: maximum task volume
• $\underline{m}$: minimum task volume

Strict Partitioning Strategy

1. Offline Partitioning
   • processor를 disjoint partitions로 나누고,
   • 각 partition에 task를 할당한다.

Definition: Strict Partitioning
$\Pi$와 $\tau$에 대해서 strict partitioning은 다음과 같은 조건을 만족한다.

• 프로세서들 $\Pi$는 disjoint subset $\rho = \{\rho_j \subseteq \Pi, \forall j\}$으로 나누어 진다.
• 각 task $\tau_k$는 오직 하나의 파티션에 할당된다.

2. Online Scheduling

   • Offline Partitioning이 정해진 후, 각 파티션은 online 스케쥴러에 의해 런타임에 스케쥴된다.
   • Global Gang scheduler와 uniprocessor task scheduler 둘다 사용될 수 있다.

Comparative Study

Pessimisms in Global Gang Schedulability Analyses

Respose Time Analysis for Real-Time Global Gang Scheduling, 2022

1. Non-Parallel Execution: NP-Hard (subset sum problem)
2. Interference Overestimation: NP-Hard (knapsack problem)

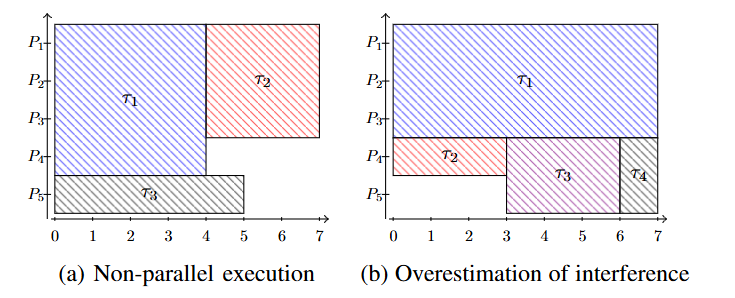
Stationary Scheduling and Strict Partitioning

• Stationary scheduling은 코어를 공유할 수 있음으로써 간접적으로 interference를 전파할 수 있다.
  • 즉 서로 겹치는 프로세서가 없음에도 Interference가 발생할 수 있다. (A to B, B to C)
• Strict Partitioning은 프로세서 할당간에 겹치는 걸 방지함으로써, 이러한 문제를 피할 수 있다.
  

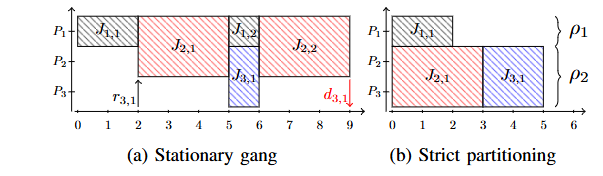
• 그러나 task들이 다른 parellelism level을 갖는 상황에서는 stationary scheduling이 더 나은 성능을 보일 수 있다.
  

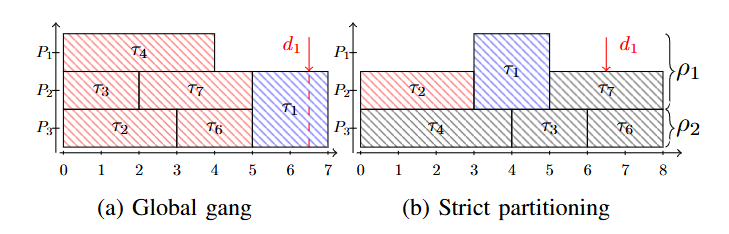
Global and Partitioned for Non-Preemptive Gangs

• rigid gakg tasks는 non-preemptive 환경에서 긴 priority-inversion을 유발할 수 있다.
• 이 문제를 완화하기 위해 static partitioning을 사용할 수 있다.
  

Strict Partitioning Algorithms

Offline Partitioning Heuristic

• Task partitioning 문제는 심지어 gang이 아닌 경우에도 NP-Hard이다.
• 따라서 offline partitioning을 위한 heuristic을 제안한다.
• FFDV (First-Fit Decreasing Volume)
  1. Task들을 volume이 감소하는 순서로, 같다면 $T_i$가 감소하는 순서로 정렬한다.
  2. 정렬된 task들을 하나씩 partition $\rho_1, \rho_2, \ldots, \rho_t$에 할당한다.
  3. 각 Task들은 그 partition에 들어가도 schedulable한 가장 처음 partition에 할당된다.
  4. 새로운 partition을 만들 수 없거다, Task를 모두 할당한 경우 알고리즘이 종료된다.
• iii.에서의 schedulability test의 시간복잡도가 $\mathcal{O}(\Omega)$라면, $\mathcal{O}(nM\Omega)$의 시간복잡도를 갖는다.

Two Strict Partitioning Variants: SP-U, SP-G

SP-U는 uniprocessor online scheduler 를 사용하고, SP-G는 global gang scheduler 를 사용한다.

• SP-U는 프로세서 활용률은 낮을 수 있지만 런타임 오버헤드가 낮고, 잘 확립된 정확한 Schedulability test가 있다.
• SP-G는 서로다른 작업이 파티션 내에서 병렬로 실행되도록 하여 프로세서를 최대한 활용할 수 있다.

두 변형 모두 FFDV를 사용하며,

• SP-U의 경우 uniprocessor schedulability test에 FFDV 휴리스틱을 그대로 적용하여 테스트를 만들고,
• SP-G의 경우 성능을 더욱 향상시키기 위해 FFDV 휴리스틱에 대한 수정을 추가한다.

Performance Bounds for SP-U

• SP-U에 대한 세 가지 Performance Bounds를 증명한다.
• 첫번째 Bound는 bin-packing 문제 자주 사용되는 weighting function으로 정의되는 weighted utilization bound이다.
• 두번째와 세번째 bound는 2D strip packing 문제에서 영감을 받은 일반적인 utilization bound이다.
  • $u_b$: uniprocessor task scheduler의 utilization bound
  • $\text{FFDV}(\tau)$: FFDV heuristic에 의해 사용되는 프로세서의 개수.
• 즉, $\text{FFDV}(\tau) \le M$을 증명하는 것으로 schedulability를 증명할 수 있다.

Theorem 1: $M$개의 프로세서를 사용하는 SP-U에 대해 Gang task set $\tau$가 다음을 만족하면 schedulable하다.

$\sum_{\tau_i \in \tau} W(U_i) \leq (M - \overline{m}) \cdot u_b, \tag{1}$

여기에서 $W: [0, u_b] \rightarrow [0, \frac 8 5 u_b]$는 다음과 같이 정의된다.

$W(U_i) = \begin{cases} \frac{6}{5} U_i, & \text{ if } 0 \leq U_i \leq \frac{1}{6} u_b; \\ \frac{9}{5} U_i - \frac{1}{10}, & \text{ if } \frac{1}{6} u_b < U_i \leq \frac{1}{3} u_b; \\ \frac{6}{5} U_i + \frac{1}{10}, & \text{ if } \frac{1}{3} u_b < U_i \leq \frac{1}{2} u_b; \\ \frac{6}{5} U_i + \frac{4}{10}, & \text{ if } \frac{1}{2} u_b < U_i \leq u_b. \end{cases}$

Proof
다음 부등식은 Performance bounds for level-oriented two-dimensional packing algorithms, 1980에서 증명되었다.

$W(U) = \sum_{\tau_i \in \tau} W(U_i) \geq (\mathrm{FFDV}(\tau) - \overline{m}) \cdot u_b. \tag{2}$

(1)과 (2)를 결합하면, 다음 식을 얻는다. 따라서, $\text{FFDV}(\tau) \leq M$이 성립한다.

$(\text{FFDV}(\tau) - \overline{m}) \cdot u_b \leq \sum_{\tau_i \in \tau} W(U_i) \leq (M - \overline{m}) \cdot u_b. \tag{3}$

Theorem 2
$M$개의 프로세서를 사용하는 SP-U에 대해 Gang task set $\tau$가 다음을 만족하면 schedulable하다.

$U \le \frac{(M - \overline{m} + \underline{m}) \cdot u_b}{2}. \tag{4}$

Proof

• $\rho_i$에 대한 total utilization을 $U_i(\rho_i)$, sequential utilization을 $u_i(\rho_i)$라고 하자.
• 그리고 $\rho_i$에 할당된 첫번째 task의 sequential utilization을 $u_i^0$이라고 하자.
• $i \ge 2$에 대해 $\rho_i$의 첫번째 task는 $\rho_{i-1}$에 들어갈 수 없다. (FFDV의 정의)
• 따라서 $u(\rho_{i-1}) + u_i^0 > u_b$가 성립한다.
• $\rho_{i-1}$의 태스크들은 적어도 $|\rho_i|$이상의 volume을 갖고, $\rho_i$의 첫번째 태스크는 $|\rho_i|$이므로,
  $U(\rho_{i-1}) + U(\rho_i) \ge (u(\rho_{i-1}) + u_i^0)|\rho_i| > |\rho_i|u_b$
  를 갖는다.

• 따라서, 다음 식이 성립한다.

  $\begin{aligned} FFDV(\tau) &= \sum_{i=1}^{t} |\rho_i| < |\rho_1| + \frac{1}{u_b} \left( \sum_{i=1}^{t-1} U(\rho_i) + \sum_{i=2}^{t} U(\rho_i) \right) \\ &= \overline{m} + \frac{2}{u_b} \sum_{i=1}^{t} U(\rho_i) - \frac{1}{u_b} (U(\rho_1) + U(\rho_t)). \end{aligned}$

• $U(\rho_1) + U(\rho_t) > \underline{m} \cdot u_b$이므로 다음이 성립한다.

  $FFDV(\tau) < \overline{m} + \frac{2}{u_b} \sum_{i=1}^{t} U(\rho_i) - \underline{m}.$

• 모든 태스크들이 $t$개의 파티션에 할당되므로, $\sum_{i=1}^{t} U(\rho_i) = U$이고, 따라서 $\text{FFDV}(\tau) \le M$이 성립한다.

Theorem 3
$M$개의 프로세서를 사용하는 SP-U에 대해 Gang task set $\tau$가 $\exists p \in \mathbb{Z}^+ \land p \ge 2$에 대해 다음을 만족하면 schedulable하다.

$u_i \le \frac{u_b}{p}, \forall \tau_i \in \tau, \tag{5}$

and

$U \le \frac{p}{p+1}(M - \overline{m})u_b. \tag{6}$

Proof

• $\rho_1 = \overline{m}$임을 알고있으므로, 다음이 성립한다. ($|\rho_{t+1}|=0$이라고 할 때)
  $\text{FFDV}(\tau) = \sum_{i=1}^{t} |\rho_{i+1}| + \bar{m}, \tag{7}$
• 따라서 다음을 증명하면 된다. (증명은 생략)
  $\frac{p}{p+1} \sum_{i=1}^{t} |\rho_{i+1}| u_b \leq U, \tag{8}$

• (6)과 (8)을 결합하면,
  $\frac{p}{p+1} \sum_{i=1}^{t} |\rho_{i+1}| u_b \le \frac{p}{p+1}(M - \overline{m})u_b$
  이 성립한다.
• 따라서
  $\sum_{i=1}^{t} |\rho_{i+1}|+\overline{m} = \text{FFDV}(\tau) \le M$
  을 만족한다.

Modifications of FFDV for SP-G

다음 두 관찰을 기반으로 FFDV 알고리즘에 대한 두 가지의 수정을 제안한다.

Observation 1
$\rho_j$에 할당된 task set $\tau(\rho_j)$에 대해,

이 성립하고, uniprocessor task scheduler에 의해 $\tau(\rho_j)$는 unschedulable하다면,
모든 global gang scheduler에 대해서 $\tau(\rho_j)$는 unschedulable하다.

• 따라서 우리는 부등식 (9)를 미리 체크해야하고, 만약 이 조건이 성립한다면, 우리는 uniprocessor task scheduler를 사용해서 schedulability test를 진행한다.
• 아니라면, 충분한 (필요조건은 아닌) schedulability test를 사용할 것이다.

• 여기에서 uniTest와 globalTest가 각각 uniprocessor task scheduler와 global gang scheduler를 이용한다.

Observation 2
SP-G에서 $\tau_i$가 이미 존재하는 $\rho_1, \rho_2, \ldots, \rho_t$에 할당될 수 없고, 남은 프로세서 $M'$가 $0<M'<m_i$ 를 만족한다면, $\tau_i$는 마지막 파티션 $\rho_t$를 $M'$까지 증가시켜서 schedulable하게 만들 가능성이 있다.

• 따라서 기존 알고리즘의 else: return False를 다음과 같이 바꿀 수 있다.
  

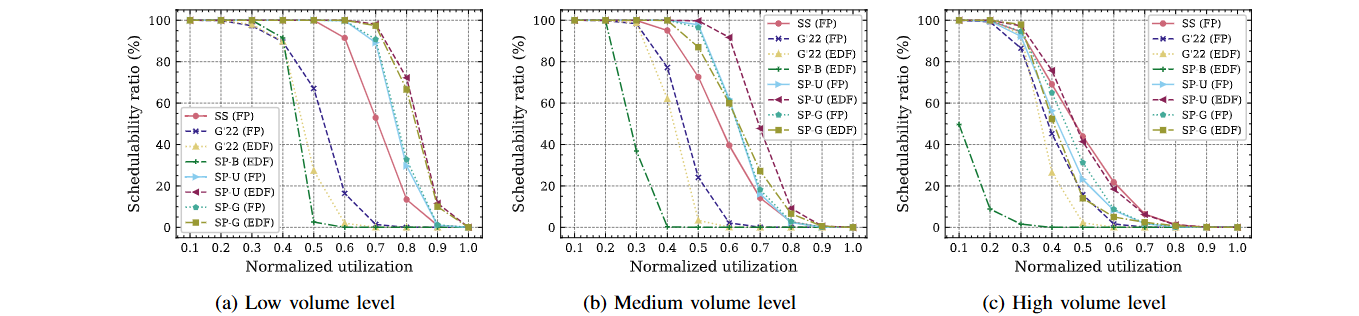
Performance Evaluation

Preemptive Scheduling

• SS(FP): Stationary Scheduling with FP
• G'22(FP/EDF): Global schedulability analysis for FP/EDF
• SP-B(EDF): Strict partitioning with EDF (Theorem 1,2,3)
• SP-U(FP/EDF): Strict partitioning with uniprocessor online scheduler
• SP-G(FP/EDF): Strict partitioning with global gang online scheduler (G'22 for globalTest)
  

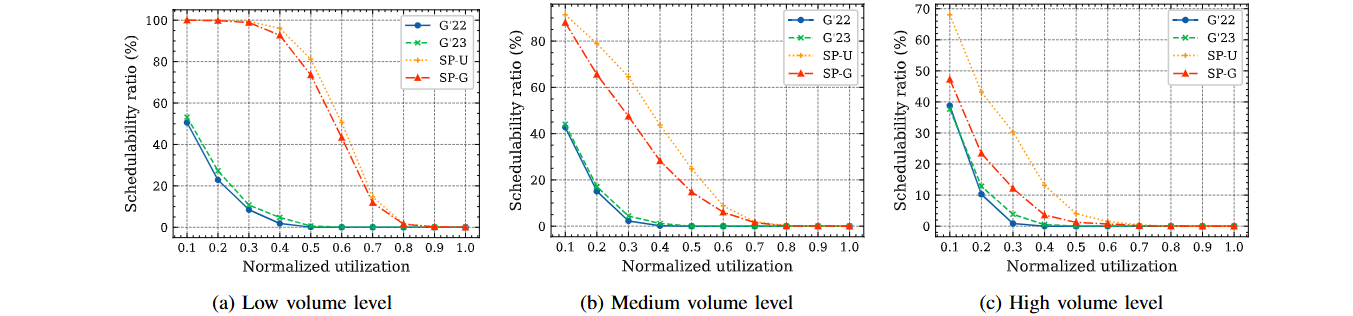
Non-Preemptive Scheduling

• G'22(FP): Global schedulability analysis for FP
• G'23(FP) : Global schedulability analysis for FP (2023)
• SP-U(FP): Strict partitioning with uniprocessor online scheduler
• SP-G(FP): Strict partitioning with global gang online scheduler (G'23 for globalTest)