📦 Gang EDF Scheduling of Parallel Task Systems

Introduction

• Gang Scheduling에 EDF를 적용하는 방법에 대해 살펴본다.
• Gang EDF를 위한 schedulability condition을 제시한다

Definitions and Assumptions

• Parallel task is:
  • $rigid$: 미리 정해져 있는 고정된 프로세서 수를 사용한다
  • $moldable$: 프로세서 수는 변할 수 있지만, 실행 전에는 결정된다.
  • $malleable$: 런타임에도 프로세서 수가 변할 수 있다.
• $\tau_i = (v_i, C_i, D_i, T_i)$: 사용하는 프로세서 수, 최대 실행 시간, 마감 기한, 주기
• $moldable$
• $C_i$ 는 각 프로세서 중 제일 오래 걸리는 작업의 시간, synchronization overhead를 포함한다
• Constrained-deadline: $D_i \le T_i$ for all $\tau_i$
• Fully independent & preemptive
• $C_i$는 $v_i$에 의해 결정되고, $v_i$는 유저나 스케줄러에 의해 결정된다.

• demand bound function $\textrm{dbf}(\tau_i, L)$:
  $\text{dbf}( \tau_i, L) = \max \left( 0, \left\lfloor \frac{L - D_i}{T_i} \right\rfloor + 1 \right) \times C_i \times v_i \tag{1}$
• horizontal-damand bound function $\textrm{hbf}(\tau_i, L)$:
  $\text{hbf}( \tau_i, L) = \max \left( 0, \left\lfloor \frac{L - D_i}{T_i} \right\rfloor + 1 \right) \times C_i = \text{dbf}(\tau_i, L) \times \frac 1 {v_i} \tag{2}$
  이는 $C_i\times v_i$ 직사각형의 너비(시간 축)으로 생각할 수 있다

Gang EDF Scheduling

• Global EDF에서는 항상 $m$개의 태스크를 선택할 수 있지만, Gang EDF에서는 공간적 제약이 필요하다.
• 먼저 $\sum_{\tau\in Q_k}v_i \le m$과 $\sum_{\tau\in Q_{k+1}}v_i > m$을 만족하는 earlist deadline의 $k$개의 태스크셋 $Q_k$을 선택한다.
• 이들은 실행에 제약이 없다.
• 여기서 우리는 $\tau_j \in Q_{k+1}\setminus Q_k$에 대해 $m-\sum_{\tau\in Q_k}v_i \;(<v_j)$만큼의 프로세서만 할당할 수 있다.

Gang scheduling vs Coscheduling

Gang EDF scheduling policy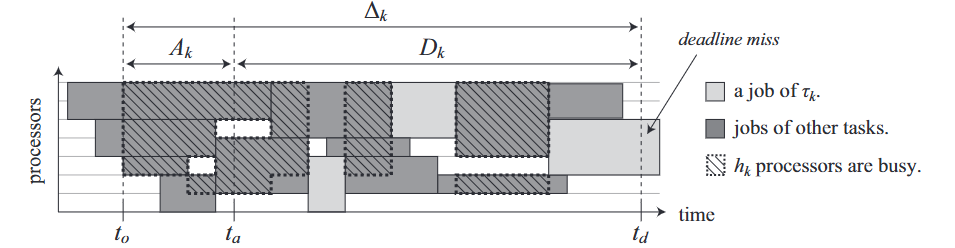

• first fit heuristic에 의해서 다음 작업을 넣을 수 있을 때 넣음.

Schedulability Analysis

• $\tau_k$가 $t_d$에 deadline miss가 발생한다고 가정. - 이를 $problem\;job$이라 부름.
• $\tau_k$의 arrival time은 $t_a = t_d - D_k$
• $t_o$는 $t_a$보다 작거나 같고, $v_k$개의 프로세서가 유휴상태인 가장 늦은 시점이라 정의한다.
• 이때 $t_d - t_o = \Delta_k$라 정의한다.
• Deadline miss가 발생하기 위해서는 $[t_a, t_d)$에서 다른 작업들의 실행이 $D_k - C_k$보다 길어야 한다.
• 또한, $\tau_k$가 $v_k$개의 프로세서를 동시에 사용해야 하기에, 적어도 $m-v_k +1$ 이상의 프로세서가 차단되는 시간이 $\Delta_k-C_k$보다 커야 한다.
• 이를 $interference\;rectangle$이라 정의한다.
  $w_k = \Delta_k - C_k \tag{3}$
  $h_k = m-v_k+1 \tag{4}$

• $I_k(\tau_i)$는 $[t_o, t_d)$에서 $\tau_i$에 의해 간섭당하는 시간을 의미하고, 앞의 식을 다음과 같이 정리할 수 있다.
  $\sum_{\tau_i \in \tau}I_k(\tau_i) > w_k \times h_k \tag{5}$
• 여기에서 만약 $\tau_i$가 $carry$-$in$ 작업이 없는 경우 $I_1(\tau_i)$라 표기하고, 있는 경우 $I_2(\tau_i)$라 표기한다.

Simple Bounds

$\tau_i$가 $carry$-$in$ 작업이 없는 경우, $I_1(\tau_i)$는 다음과 같이 구할 수 있다.

• $i \neq k$ 인 경우, $\tau_i$의 간섭 사각형에 대한 수평 기여도는 최대 $\textrm{hbf}(\tau_i, \Delta_k)$이며,
• 이는 $\tau_k$의 간섭 사각형 너비를 초과할 수 없으므로, $\tau_k$의 간섭 사각형에 대한 수평기여도는 다음과 같다.
  $\min\{\textrm{hbf}(\tau_i, \Delta_k), w_k\}$
• 비슷한 이유로 간섭 사각형에 대한 수직 기여도는 다음과 같다.
  $\min\{v_i, h_k\}$
• $i=k$인 경우, 수평적 기여는 $A_k = \Delta_k - D_k$를 넘을 수 없다.
• 이를 정리하여 $I_1(\tau_i)$를 나타내면:
  $I_1(\tau_i) = \begin{cases} \min\{\text{hbf}(\tau_i, \Delta_k), w_k\} \times \min(v_i, h_k) & \text{if } i \neq k \\ \min\{\text{hbf}(\tau_i, \Delta_k) - C_k, A_k\} \times \min(v_i, h_k) & \text{otherwise} \end{cases} \tag{6}$

$\tau_i$가 $carry$-$in$ 작업이 있는 경우, $I_2(\tau_i)$는 다음과 같이 구할 수 있다.

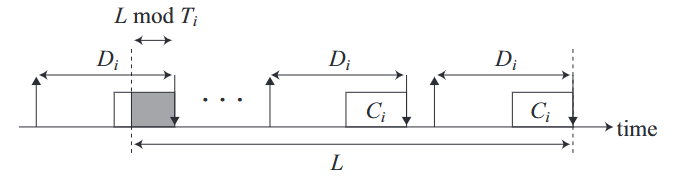
• $\tau_i$의 어떤 작업의 deadline이 구간 $L$의 끝에 있고, $\tau_i$의 모든 작업이 preemption없이 deadline전에 수행될 때의 horizontal demand를 $\textrm{hbf}'(\tau_i, L)$ 이라고 하자.

• 이는 위 그림을 통해 $carry$-$in$ 작업의 양이 최대 $\min(C_i, L \mod T_i)$ 이고, 구간 내 작업의 개수는 $\lfloor L/T_i\rfloor$임을 알 수 있다.

• 따라서 $\textrm{hbf}'(\tau_i, L)$는 다음과 같다.

  $\text{hbf}'(\tau_i, L) = \left\lfloor \frac{L}{T_i} \right\rfloor \times C_i + \min(C_i, L \mod T_i)\tag{7}$

• $\textrm{hbf}'(\tau_i, L)$이 위와 같으므로 $I_2(\tau_i)$는 다음과 같이 구할 수 있다.

Improved Bounds

• $Eq. (6)$은 $\tau_i$의 간섭을 과대평가한다는 점에서 비관적이다.
  $I_1(\tau_i) = \begin{cases} \min\{\text{hbf}(\tau_i, \Delta_k), w_k\} \times \min(v_i, h_k) & \text{if } i \neq k \\ \min\{\text{hbf}(\tau_i, \Delta_k) - C_k, A_k\} \times \min(v_i, h_k) & \text{otherwise} \end{cases} \tag{6}$

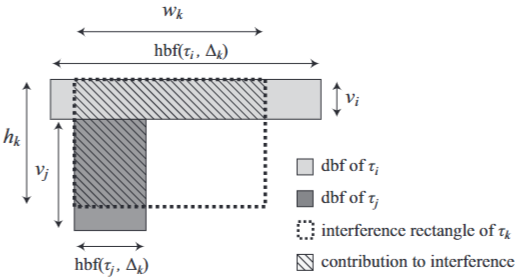
Lemma 1
두 태스크 $\tau_i$와 $\tau_j$에 대해서 $h_k - v_i \leq v_j \leq h_k$ 및 $\text{hbf}(\tau_j, \Delta k) \leq w_k \leq \text{hbf}(\tau_i, \Delta k)$가 성립할 때 $\tau_k$의 간섭사각형에 대한 $I_1(\tau_j) + I_1(\tau_i)$는 최대 다음과 같다.

$w_k \times v_i + \text{hbf}(\tau_j, \Delta_k) \times (h_k - v_i) \tag{9}$

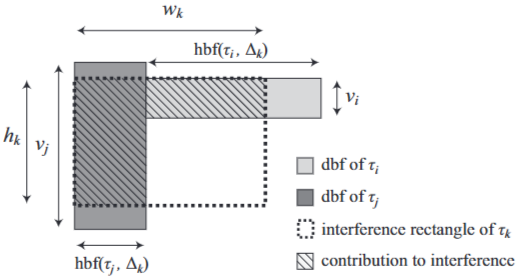
Lemma 2
두 작업 $\tau_i$와 $\tau_j(i \neq j \neq k)$에 대해, $v_i \leq h_k \leq v_j$ 및 $w_k - \text{hbf}(\tau_j, \Delta k) \leq \text{hbf}(\tau_i, \Delta k) \leq w_k$인 경우 $\tau_k$의 간섭사각형에 대한 $I_1(\tau_j) + I_1(\tau_i)$는 최대 다음과 같다.

$\{ w_k - \text{hbf}( \tau_j, \Delta_k ) \} \times v_i + \text{hbf}( \tau_j, \Delta_k ) \times h_k \tag{10}$

이 두 보조정리는 다음 보조정리로 이어지게 된다.

Lemma 3
$w_k \times h_k$ 간섭 사각형은 $\text{hbf}(\tau_i, \Delta_k) \ge w_k$인 $\tau_i$가 존재할 때, $w_k \times (h_k-v_i)$로 축소할 수 있다.

Lemma 4
$w_k \times h_k$ 간섭 사각형은 $v_i \ge h_k$인 $\tau_i$가 존재할 때, $\{w_k-\text{hbf}(\tau_i, \Delta_k)\} \times h_k$로 축소할 수 있다.

따라서 우리는 앞의 $Eq. (6)$을 아래와 같이 바꿀 수 있다.

• $\alpha_1=\{\tau_{i\neq k}\in\tau | \text{hbf}(\tau_i, \Delta_k) \ge w_k\}$라 할 때,

• $\displaystyle h_k(\alpha_1) = h_k - \sum_{\tau_i \in \alpha_1}v_i$로 축소할 수 있고,

• $\beta_1=\{\tau_{i}\notin\alpha_1 | v_i \ge h_k(\alpha_1)\}$라 할 때,

• $\displaystyle w_k(\beta_1) = w_k - \sum_{\tau_i \in \beta_1}\text{hbf}(\tau_i, \Delta_k)$로 축소할 수 있다.

• 우리는 이러한 크기 축소를 계속 반복할 수 있다.
• 그러면 $h_k(\alpha_0)=h_k$, $w_k(\beta_0)=w_k$로 시작하여, 다음 식을 반복할 수 있다.

• 이 과정을 $\alpha_s$나 $\beta_s$가 공집합일때까지 반복하였을 때,
• 그 어느 $\alpha_s$또는 $\beta_s$에 대해서도 포함되지 않은 태스크들의 집합을 $\gamma$라 하자.

• 최종적으로 간섭 사각형은 $w_k(\alpha_{\max})\times h_k(\beta_{\max})$ 로 축소된다.
• 그리고 $\gamma$의 정의에 따라 $\forall \tau_i \in \gamma$는 $\text{hbf}(\tau_i, \Delta_k) < w_k(\beta_{\max})$, $v_i < h_k(\alpha_{\max})$를 만족한다.
• 또한 $\alpha_s$에 포함된 집합은 $\text{hbf}(\tau_i, \Delta_k) \ge w_k(\beta_{s-1})$를 만족하고, $\beta_s$에 포함된 집합은 $v_i \ge h_k(\alpha_s)$를 만족한다.
• 따라서 우리는 $I_1$을 다음과 같이 변경할 수 있다.

$carry$-$in$ 작업이 있는 경우도 비슷하게 진행할 수 있다.

$\gamma'$도 똑같이 정의하면,

다음과 같이 $I_2$를 변경할 수 있다.

Schedulability Condition

• $I_\text{diff}(\tau_i)$를 다음과 같이 정의하면, 이는 $\tau_i$에 의한 $carry$-$in$ 작업의 간섭 사각형에 대한 기여임이 자명하다.
  $I_{\text{diff}}(\tau_i) = I_2(\tau_i) - I_1(\tau_i) \tag{23}$
• 따라서, $I_\text{carry-in}$을 모든 $carry$-$in$ 작업의 간섭 사각형에 대한 기여로 정의하면, 다음과 같은 식을 얻는다.
  $I_{\text{carry-in}} = \begin{cases} \max \left\{ \sum_{\tau_i \in \sigma} I_{\text{diff}}(\tau_i) \right\} & \text{if } \exists \sigma \subset \tau \\ \max \left\{ I_{\text{diff}}(\tau_i) \right\} & \text{otherwise} \end{cases} \tag{24}$
  여기서 $\sigma$는 $\sum_{\tau_i \in \sigma}v_i \le m-v_k$를 만족하는 임의의 부분집합이다.
• 우리는 여기서 $\sigma$에 대한 계산을 해야하지만 이는 Knapsack 문제와 유사하며 이는 NP-hard임이 알려져있다.

이를 좀 더 쉽게 하기 위해 $I_\text{carry-in}$을 약간 과대평가해보자.

• $\tau$의 복제본 $\tau'$가 $I_\text{diff}(\tau_i)/v_i$를 기준으로 내림차순 정렬되어있다고 하자. 그리고 같으면 $v_i$에 대해 정렬하자.
• 이때 $\tau_\text{carry-in}$를 다음을 만족하는 가장 첫번째 부분집합으로 선택하자.
  $\sum_{\tau_i \in \tau_{\text{carry-in}}} v_i \geq m - v_k$

• $I_\text{carry-in}$을 $\tau_\text{carry-in}$로부터 구할 때, 간섭 사각형을 세로로 초과하는 vertical demand, 즉 $m-v_k$를 초과하는 부분은 고려할 필요가 없다.
• 이때 $\tau_\text{carry-in}$의 마지막 태스크 $\tau_l$이 실제로 사용할 수 있는 프로세서 수 $n'_l$는 다음과 같다.
  $n'_{l} = m - v_k - \sum_{\tau_i \in \tau_{\text{carry-in}} \setminus \tau_l} v_i.$
• 따라서 우리는 $Eq (24).$ 대신 아래와 같이 표현할 수 있다.
  $I_\text{carry-in} = \sum_{\tau_i \in \tau_\text{carry-in}} I_\text{diff}(\tau_i) - (v_l - n'_l) \times I_\text{diff}(\tau_l) \tag{25}$
• 그러므로 원래의 $Eq (5)$를
  $\sum_{\tau_i \in \tau} I_k(\tau_i) > w_k \times h_k \tag{5}$
• 다음과 같이 변경할 수 있다.
  $\sum_{\tau_i \in \tau} I_1(\tau_i) + I_{\text{carry-in}} > w_k \times h_k \tag{26}$

Theorem 1
모든 작업 $\tau_k \in \tau$ 및 모든 $\Delta_k \geq D_k$에 대해 다음 조건이 충족되면 작업 시스템 $\tau$가 $m$ 프로세서에서 Gang EDF에 의해 성공적으로 스케줄링되는 것이 보장된다.

$\sum_{\tau_i \in \tau} I_1(\tau_i) + I_{\text{carry-in}} \leq w_k \times h_k \tag{27} ?$

• 마지막으로 $\Delta_k$의 범위를 유한한 범위로 줄이기 위해 Theorem 2를 제안한다.

Theorem 2
만약 어떤 $\Delta_k \ge D_k$에 대해 조건 $(27)$이 위반된다면, 이는 다음을 만족하는 $\Delta_k$에 의해 위반된 것이다.

$\Delta k \leq \frac{h_{k} C_{k} - \sum_{\tau_{i} \in \tau} \left\{ (D_{i} - T_{i}) U_{i} \times \min(v_{i}, h_{k}) \right\} + C_{\text{carry-in}}}{h_{k} - \sum_{\tau_{i} \in \tau} U_{i} \times \min(v_{i}, h_{k})} \tag{28}$

Proof

$I_{1}(\tau_{i}) \leq \text{hbf}(\tau_{i}, \Delta_{k}) \times \min(v_{i}, h_{k}) \leq (\Delta_{k} - D_{i} + T_{i}) \times U_{i} \times \min(v_{i}, h_{k}).$

또한 $carry$-$in$은 최대 $C_i$이므로, 다음 또한 유도할 수 있다.

$I_{2}(\tau_{i}) \leq I_{1}(\tau_{i}) + C_{i} \times \min(v_{i}, h_{k}).$

조건 $(27)$을 위반시키면 아래와 같이 정리된다.

$\begin{aligned} &\sum_{\tau_i \in \tau} \text{hbf}( \tau_i , \Delta_k ) \times \min( v_i , h_k ) + C_{\text{carry-in}} > w_k \times h_k \\ \Rightarrow &\sum_{\tau_i \in \tau} \{ ( \Delta_k - D_i + T_i ) \times U_i \times \min( v_i , h_k ) \} + C_{\text{carry-in}} > ( \Delta_k - C_k ) \times h_k \\ \Rightarrow &\Delta_k \leq \frac{h_k C_k - \sum_{\tau_i \in \tau} \{ ( D_i - T_i ) U_i \times \min( v_i , h_k ) \} + C_{\text{carry-in}}}{h_k - \sum_{\tau_i \in \tau} U_i \times \min( v_i , h_k )} \end{aligned}$

$\blacksquare$