📦️ TTN: A Domain-Shift Aware Batch Normalization in Test-Time Adaptation

Contributions

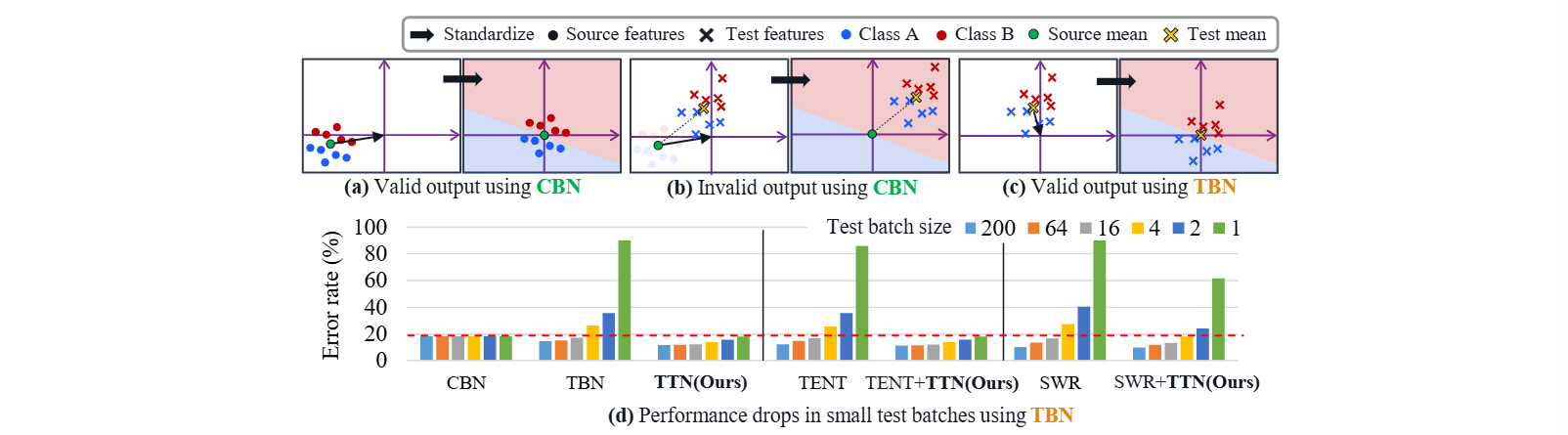
• 채널별 보간 가중치를 사용하여 Source batch statistics(CBN)와 Test batch statistics(TBN)를 결합하며, 새로운 도메인에 대해 적응하면서도 원천지식을 보존하는 TTN 레이어를 제안한다.
• 기존의 TTA 방법에 TTN을 추가하면 테스트 배치 크기(1에서 200까지)의 폭넓은 범위에서 성능이 크게 향상됨을 보인다.

2. Methodology

2.1. Problem Setup

• 훈련 데이터와 테스트 데이터를 $\mathcal{D}_S,\;\mathcal{D}_T$, 각각에 대한 확률분포를 $P_S,\;P_T$라 하자.
• TTA의 Covariate Shift는 $P_S \neq P_T$ where $P_S(y|x) = P_T(y|x)$이다.
• 모델 $f_\theta$는 $\mathcal{D}_S$의 mini-batch $\mathcal{B}^S = \left\{(x_i, y_i)\right\}^{|\mathcal{B}^S|}_{i=1}$로 학습되었으며,
• 테스트 중에는 $f_\theta$는 테스트 배치 $\mathcal{B}_T\sim\mathcal{D}_T$를 만나게 된다.
• 그리고 TTA의 목표는 다른 분포로부터 테스트 배치를 올바르게 처리하는 것이다.

좀 더 실용적인 TTA를 시뮬레이션하기 위해 우리는 두 개의 변화를 중점적으로 고려한다.

1. 다양한 테스트 배치의 크기 $|\mathcal{B}^T|$ - 작은 배치사이즈는 짧은 지연으로 이어진다.
2. 여러 개, $N$ 개의 도메인 $\mathcal{D}_T = \{\mathcal{D}_{T,i}\}^N_{i=1}$으로의 적응

2.2. Test-Time Normalization Layer

• BN 레이어의 입력을 $\mathrm{z}\in\mathbb{R}^{BCHW}$라 하자. (배치 사이즈 $B$, 채널 수 $C$, 높이와 너비 $H,W$)
• $\mathrm{z}$의 평균과 분산은 $\mu$와 $\sigma^2$이고, 각각은 다음과 같이 나타난다.
  $\mu_c = \frac 1 {BHW} \sum^B_b\sum^H_h\sum^W_w\mathrm{z}_{bchw},\qquad \sigma_c^2 = \frac 1 {BHW} \sum^B_b\sum^H_h\sum^W_w(\mathrm{z}_{bchw}-\mu_c)^2 \tag{1}$
• BN레이어에서 $\mathrm{z}$는 먼저 $\mu$와 $\sigma^2$로 표준화된 뒤, 학습 가능한 파라미터 $\gamma, \beta \in \mathbb{R}^C$로 affine 변환된다.
• 표준화는 현재 input batch statistics를 훈련 중에 사용하고, 테스트 중에는 추정된 source statistics $\mu_s$와 $\sigma_s^2$를 사용한다.
• 또한 domain shift를 고려하기 위해, 학습 가능한 보간 가중치 $\alpha \in \mathbb{R}$을 이용하여 source batch statistics와 test batch statistics를 결합한다.
  $\tilde{\mu} = \alpha \mu + (1 - \alpha) \mu_s, \quad \tilde{\sigma}^2 = \alpha \sigma^2 + (1 - \alpha) \sigma_s^2 + \alpha (1 - \alpha)(\mu - \mu_s)^2 \tag{2}$

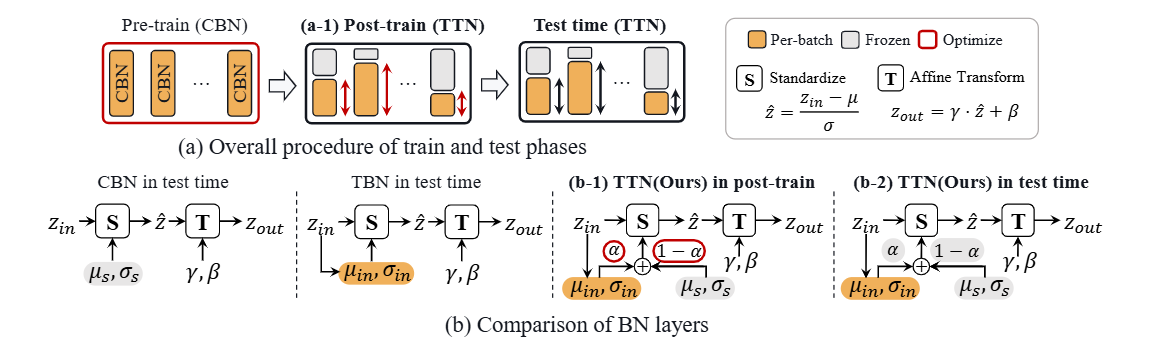
• 위 그림에서 볼 수 있듯, CBN과 TBN을 $\alpha$로 결합하여 사용한다.
• $\alpha$는 post-train 단계에서 학습되고, 이후 고정된다.
• 이 과정을 통해 각 채널과 레이어마다 다른 $\alpha_c$를 갖게 된다.

2.3. Post Training

앞에서 말한 $\alpha$를 학습시키는 post-training에 대해 설명한다.

• $\alpha$를 제외한 모든 파라미터는 고정되며, post-training 과정에는 source data에 접근할 수 있다.
• 먼저 어떤 레이어와 채널이 domain shift에 민감한지를 나타내는 $\alpha$의 사전지식 $\mathcal{A}$를 구한다.
• 그 후, 사전 지식과 추가적인 Objective term을 이용하여 $\alpha$를 최적화한다.

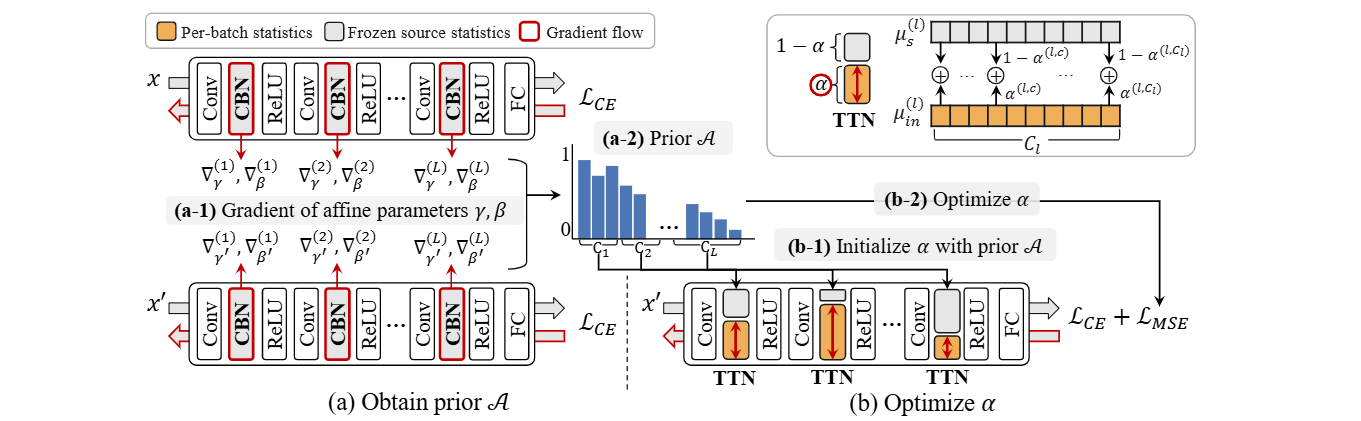
2.3.1 Obtain Prior $\mathcal{A}$

• Augmentation을 통해 source data에 대한 domain shift를 시뮬레이션한다.($x'$)
• 먼저 어떤 레이어와 채널의 표준화 수치가 올바르게 되어야 하는지 알기 위해 $z^{(l, c)}$의 standardized feature $\hat{z}^{(l,c)}$를 구한다.
• 이를 domain-shift된 $\hat{z}'^{(l,c)}$와 비교한다.
• 사전 학습된 CBN이 두 입력에 대해 동일한 $\mu_s^{(l, c)}$, $\sigma_s^{(l, c)}$를 사용하므로, $\hat{z}'^{(l,c)}$와 $\hat{z}^{(l,c)}$의 차이는 $x$와 $x'$의 차이로 인해 발생한다.
• 만약 이 차이가 크다면 $(l, c)$는 domain shift에 민감하다고 판단할 수 있다.
• 이를 어파인 파라미터 $\gamma, \beta$의 gradient $\nabla_\gamma, \nabla_\beta$ 를 비교함으로써 측정할 수 있다.
• 그리고 위 그림에서 볼 수 있듯, 우리는 cross-entropy loss $\mathcal{L}_{CE}$를 이용해서 $\nabla_\gamma, \nabla_\beta$ 를 얻을 수 있다.

• 최종적으로, gradient distance score $d^{(l,c)} \in \mathbb{R}$을 다음과 같이 정의한다.

• 여기서 $(g,g')$는 $s_\gamma^{(l,c)}$와 $s_\beta^{(l,c)}$에 대해 $(\nabla_\gamma^{(l,c)}, \nabla_{\gamma'}^{(l,c)})$, $(\nabla_\beta^{(l,c)}, \nabla_{\beta'}^{(l,c)})$를 의미한다.
• $N$은 훈련 데이터 수를 의미하므로 $d^{(l,c)}$는 $[0,1]$의 값을 갖는다.
• 상대적인 차이를 강조하기 위해, 우리는 최종적으로 제곱을 취하여 사전지식 $\mathcal{A}$를 구한다.
  $\mathcal{A} = [d^{(1,.)}, d^{(2,.)}, \ldots, d^{(L,.)}]^2, \tag{5}$
• 여기서 $d^{(l,.)}$는 $[d^{(l,c)}]^{C_l}_{c=1}$을 의미한다.

2.3.2 Optimize $\alpha$

• 사전 $\mathcal{A}$가 얻어진 이후에 우리는 어파인 파라미터를 유지한 채로 CBN을 TTN레이어로 대체할 수 있다.
• 그다음 $\alpha$를 $\mathcal{A}$로 초기화한다.
• 분포 변화를 시뮬레이션하기 위해, 우리는 augmented training data를 사용한다.
• 모델이 본래 input과 augmented input에 대해 동일한 성능을 내도록 $\alpha$를 최적화하기 위해 cross-entropy loss $\mathcal{L}_{CE}$를 사용한다.
• 또한 $\alpha$가 본래 $\mathcal{A}$에서 너무 멀어지지 않도록, mean-squared error loss $\mathcal{L}_{MSE} = \lVert\alpha-\mathcal{A}\rVert^2$를 추가한다.
• 최종 loss $\mathcal{L}$은 $\mathcal{L} = \mathcal{L}_{CE} + \lambda \mathcal{L}_{MSE}\;(6)$로 정의되며, $\lambda$는 weighting hyperparameter이다.