D. DP의 이론적 기초

Bard·2023년 12월 27일
AIRL

Reinforcement Learning

목록 보기
4/10
post-thumbnail

Preliminaries

Normed Vector Spaces

Normed Vector Spaces (놈 공간)은 vector space X\mathcal{X}와 X\mathcal{X}의 원소에 대한 norm ∥⋅∥\Vert \cdot \Vert으로 정의된다.

Norm은 매핑 X→R\mathcal{X} \rarr \Bbb{R}으로 정의된다.

단, 다음 조건들을 만족해야 한다.

  1. ∥x∥≥0,  ∀x∈X\Vert x\Vert \ge 0,\;\forall x \in \mathcal{X} 와 ∥x∥=0⇒x=0\Vert x\Vert=0 \rArr x = 0
  2. ∥αx∥=∣α∣∥x∥\Vert\alpha x\Vert = |\alpha|\Vert x\Vert (homogeneity)
  3. ∥x1+x2∥≤∥x1∥+∥x2∥\Vert x_1 + x_2\Vert \le \Vert x_1\Vert + \Vert x_2\Vert (triangle inequality, 삼각부등식)

이 수업에서는 아래와 같이 표기한다.

  • Vector spaces: X=Rd\mathcal{X} = \Bbb{R}^d
  • Norms:
    • max-norm/L∞L_\infin norm ∥⋅∥∞\Vert\cdot\Vert_\infin
    • (weighted) L2L_2 norm: ∥⋅∥2,ρ\Vert\cdot\Vert_{2,\rho}

Contraction Mapping

X\mathcal{X}가 norm ∥⋅∥\Vert\cdot\Vert를 갖는 벡터공간일 때, 매핑 T:X→X\mathcal{T}:\mathcal{X} \rarr \mathcal{X}이 x1,x2∈X,∃α∈[0,1]x_1, x_2 \in \mathcal{X}, \exist\alpha \in [0,1]에 대하여

∥Tx1−Tx2∥≤α∥x1−x2∥\Vert \mathcal{T}x_1 - \mathcal{T}x_2\Vert\le \alpha\Vert x_1 -x_2\Vert

를 만족한다면 이를 α\alpha-contraction 매핑이라고 한다.

  • 만약 α∈[0,1]\alpha \in [0,1]라면 우리는 T\mathcal{T}를 non-expanding이라고 부른다.
  • 모든 contraction은 정의에 의하여 Lipshitz이기도 하며, 그러므로 연속함수이다. 좀 더 구체적으로는 이런 뜻이다.
    xn→∥⋅∥x⇒Txn→∥⋅∥Txx_n \rarr _{\Vert\cdot\Vert}x \Rarr \mathcal{T}x_n \rarr _{\Vert\cdot\Vert}\mathcal{T}x

Fixed point

점이나 벡터 x∈Xx \in \mathcal{X}가 연산자 T\mathcal{T}에 대하여 Tx=x\mathcal{T}x = x를 만족한다면 이를 fixed point라 한다.

Banach Fixed Point Theorem

X\mathcal{X}가 완전한 normed vector space라고 하자. 그리고 이 X\mathcal{X}는 norm ∥⋅∥\Vert\cdot\Vert와 γ\gamma-contraction mapping인 T:X→X\mathcal{T}:\mathcal{X} \rarr \mathcal{X}를 갖는다면,

  • T\mathcal{T}는 유일한 고정점 x∈X:∃!x∗∈X s.t. Tx∗=x∗x\in\mathcal{X}: \exist! x^* \in\mathcal{X} \text{ s.t. } \mathcal{T}x^* = x^*를 갖는다.

  • ∀x0∈X\forall x_0 \in \mathcal{X}에 대해, 수열 xn+1=Txnx_{n+1}=\mathcal{T}x_n은 다음 경향을 따라 x∗x^*로 수렴한다.

    ∥xn−x∗∥≤γn∥x0−x∗∥\Vert x_n - x^* \Vert \le \gamma^n\Vert x_0 - x^*\Vert

    따라서 lim⁡n→∞∥xn−x∗∥≤lim⁡n→∞(γn∥x0−x∗∥)=0\lim\limits_{n\rarr\infin}\Vert x_n - x^* \Vert \le \lim\limits_{n\rarr\infin}(\gamma^n \Vert x_0 - x^* \Vert) = 0 이 성립한다.

Bellman Operators

The Bellman Optimality Operator

Bellman Optimality Operator TV∗T^*_\mathcal{V}
MDP M=⟨S,A,p,r,γ⟩\mathcal{M} = \lang\mathcal{S}, \mathcal{A},p,r,\gamma\rang이 주어졌을 때, V≡VS\mathcal{V} \equiv \mathcal{V}_\mathcal{S}를 S\mathcal{S}에 대한 유계 실수 함수들의 공간이라고 하자.

이때 우리는 각각에 대하여 다음과 같이 Bellman Optimality Operator TV∗:V→VT^*_\mathcal{V}: \mathcal{V}\rarr\mathcal{V}를 정의할 수 있다.

(TV∗f)(s)=max⁡a[r(s,a)+γ∑s′p(s′∣a,s)f(s′)],∀f∈V(T^*_\mathcal{V}f)(s) = \max\limits_a \left[r(s,a) + \gamma \sum \limits_{s'}p(s'|a,s)f(s')\right], \forall f \in \mathcal{V}

일반적으로는 index V\mathcal{V}를 떼어버리고 간단히 T∗=TV∗T^* = T^*_\mathcal{V}로 쓴다.

Properties of the Bellman Operator T∗T^*

  1. 유일한 고정점 v∗v^*를 갖는다.

    T∗v∗=v∗T^*v^*=v^*

  2. T∗T^*는 ∥⋅∥∞\Vert\cdot\Vert_\infin에 대하여 γ\gamma-contraction이다.

    ∥T∗v−T∗u∥∞≤γ∥v−u∥∞,∀u,v∈V\Vert T^*v-T^*u\Vert_\infin \le \gamma \Vert v-u \Vert_\infin, \forall u, v \in \mathcal{V}

  3. T∗T^*는 단조성을 갖는다.

    ∀u,v∈V s.t. u≤v⇒T∗u≤T∗v\forall u,v \in \mathcal{V} \text{ s.t. } u\le v \Rarr T^*u \le T^*v

Value Iteration through the lens of the Bellman Operator

이 Bellman Operator를 사용하면 훨씬 간단하게 VI를 나타낼 수 있다.

  • v0v_0로 시작한다.
  • 값을 다음 식을 통해 업데이트한다. vk+1=T∗vkv_{k+1} = T^* v_k

여기에서 k→∞,vk→∥⋅∥∞v∗k \rarr \infin, v_k \rarr _{\Vert\cdot\Vert_\infin}v^*를 증명할 수 있다.

간단히 바나흐 고정점 정리를 적용하기만 하면 된다.

∥vk−v∗∥∞=∥T∗vk−1−v∗∥∞    =∥T∗vk−1−T∗v∗∥∞      ≤γ∥vk−1−v∗∥∞  ≤γk∥v0−v∗∥∞\Vert v_k - v^*\Vert_\infin = \Vert T^*v_{k-1} - v^*\Vert_\infin\qquad\qquad\\\;\\ \qquad\;= \Vert T^* v_{k-1} - T^*v^*\Vert_\infin \\\;\\ \;\;\le \gamma\Vert v_{k-1} - v^*\Vert_\infin \\\;\\ \le \gamma^k \Vert v_0 - v^*\Vert_\infin

The Bellman Expectation Operator

Bellman Expectation Operator TVπT^\pi_\mathcal{V}
MDP M=⟨S,A,p,r,γ⟩\mathcal{M} = \lang\mathcal{S}, \mathcal{A},p,r,\gamma\rang이 주어졌을 때, V≡VS\mathcal{V} \equiv \mathcal{V}_\mathcal{S}를 S\mathcal{S}에 대한 유계 실수 함수들의 공간이라고 하자.

이때 우리는 임의의 정책 π:S×A→[0,1]\pi: \mathcal{S} \times \mathcal{A} \rarr [0,1]에 대하여 다음과 같이 Bellman Expectation Operator TVπ:V→VT^\pi_\mathcal{V}: \mathcal{V}\rarr\mathcal{V}를 정의할 수 있다.

(TVπf)(s)=∑aπ(s,a)[r(s,a)+γ∑s′p(s′∣a,s)f(s′)],∀f∈V(T^\pi_\mathcal{V}f)(s) = \sum\limits_a \pi(s,a)\left[r(s,a) + \gamma \sum \limits_{s'}p(s'|a,s)f(s')\right], \forall f \in \mathcal{V}

Properties of the Bellman Operator TπT^\pi

  1. 유일한 고정점 vπv^\pi를 갖는다.

    Tπvπ=vπT^\pi v^\pi=v^\pi

  2. TπT^\pi는 ∥⋅∥∞\Vert\cdot\Vert_\infin에 대하여 γ\gamma-contraction이다.

    ∥Tπv−Tπu∥∞≤γ∥v−u∥∞,∀u,v∈V\Vert T^\pi v-T^\pi u\Vert_\infin \le \gamma \Vert v-u \Vert_\infin, \forall u, v \in \mathcal{V}

  3. TπT^\pi는 단조성을 갖는다.

    ∀u,v∈V s.t. u≤v⇒Tπu≤Tπv\forall u,v \in \mathcal{V} \text{ s.t. } u\le v \Rarr T^\pi u \le T^\pi v

Policy Evaluation

  • v0v_0로 시작한다.
  • 값을 다음 식을 통해 업데이트한다. vk+1=Tπvkv_{k+1} = T^\pi v_k

여기에서 위에서와 같은 방법으로 k→∞,vk→∥⋅∥∞vπk \rarr \infin, v_k \rarr _{\Vert\cdot\Vert_\infin}v^\pi를 증명할 수 있다.

Similarly for qπ:S×A→Rq^\pi: \mathcal{S} \times \mathcal{A} \rarr \Bbb{R}

Bellman Expectation Operator TQπT^\pi_\mathcal{Q}
MDP M=⟨S,A,p,r,γ⟩\mathcal{M} = \lang\mathcal{S}, \mathcal{A},p,r,\gamma\rang이 주어졌을 때, Q≡QS,A\mathcal{Q} \equiv \mathcal{Q}_{\mathcal{S}, \mathcal{A}}를 S×A\mathcal{S}\times\mathcal{A}에 대한 유계 실수 함수들의 공간이라고 하자.

이때 우리는 임의의 정책 π:S×A→[0,1]\pi: \mathcal{S} \times \mathcal{A} \rarr [0,1]에 대하여 다음과 같이 Bellman Expectation Operator TQπ:Q→QT^\pi_\mathcal{Q}: \mathcal{Q}\rarr\mathcal{Q}를 정의할 수 있다.

(TQπf)(s)=r(s,a)+γ∑s′p(s′∣a,s)∑a′∈Aπ(a′∣s′)f(s′,a′),∀f∈Q(T^\pi_\mathcal{Q}f)(s) = r(s,a) + \gamma \sum\limits_{s'} p(s'|a,s)\sum \limits_{a'\in\mathcal{A}}\pi(a'|s')f(s',a'), \forall f \in \mathcal{Q}

이 연산자 또한 유일한 고정점을 가지며, Tπ\mathcal{T}^\pi와 같이 γ\gamma-contraction과 단조성을 갖는다.

Similarly for q∗:S×A→Rq^*: \mathcal{S} \times \mathcal{A} \rarr \Bbb{R}

Bellman Optimality Operator TQ∗T^*_\mathcal{Q}
MDP M=⟨S,A,p,r,γ⟩\mathcal{M} = \lang\mathcal{S}, \mathcal{A},p,r,\gamma\rang이 주어졌을 때, Q≡QS,A\mathcal{Q} \equiv \mathcal{Q}_{\mathcal{S}, \mathcal{A}}를 S×A\mathcal{S}\times\mathcal{A}에 대한 유계 실수 함수들의 공간이라고 하자.

이때 우리는 다음과 같이 Bellman Optimality Operator TQ∗:Q→QT^*_\mathcal{Q}: \mathcal{Q}\rarr\mathcal{Q}를 정의할 수 있다.

(TQ∗f)(s)=r(s,a)+γ∑s′p(s′∣a,s)max⁡a′∈Af(s′,a′),∀f∈Q(T^*_\mathcal{Q}f)(s) = r(s,a) + \gamma \sum\limits_{s'} p(s'|a,s)\max\limits_{a'\in\mathcal{A}}f(s',a'), \forall f \in \mathcal{Q}

이 연산자도 유일한 고정점을 가지며, T∗\mathcal{T}^*와 같이 γ\gamma-contraction과 단조성을 갖는다.

Approximate Dynamic Programming

지금까지 우리는 MDP에 대한 완벽한 지식과, value function에 대한 완벽한 표현을 갖고 있다고 가정했었다.

그러나 실제로는 아닌 경우가 훨씬 빈번하다.

  • 우리는 MDP를 알 수가 없다.
    • sampling/estimation 에러
  • 우리는 value function을 각 업데이트마다 완벽하게 알 수가 없다.
    • approximation 에러

따라서 여기에서 우리의 목표는 위 환경 속에서 최적과 근접한 정책 π\pi를 찾는 것이 될 것이다.

Approximate Value Iteration

Approximate Value Iteration은 Approximation 연산자 A\mathcal{A}를 도입하여 업데이트 함수를 다음과 같이 나타낸다.

vk+1=AT∗vkv_{k+1} = \mathcal{A}T^*v_k

그러면 여기에서도 k→∞,vk→∥⋅∥∞v∗k \rarr \infin, v_k \rarr _{\Vert\cdot\Vert_\infin}v^*가 성립할까?

일반적으로는 아니다.

ADP: Approximating the value function

θ∈Rm\theta\in\Bbb{R}^m에 대해 function approximater vθ(s)v_\theta(s)를 사용한다고 하자.

이때 kk 스텝에 대한 value function은 vk=vθkv_k = v_{\theta_k}가 될 것이다.

물론 여기서도 마치 MDP를 알고있던 것처럼 vθk+1v_{\theta_{k+1}}를 구하기 위해같은 방식으로 dynamic programming을 사용할 것이다.

T∗vk(s)=max⁡aE[Rt+1+γvk(St+1)∣St=s]T^* v_k (s) = \max\limits_a \Bbb{E}[R_{t+1} + \gamma v_k(S_{t+1}) | S_t = s]

그러나 여기에서는 θk+1\theta_{k+1}을 vθk+1≈T∗vk(s)v_{\theta_{k+1}} \approx T^* v_k (s)가 되도록 맞춰나갈 것이다.

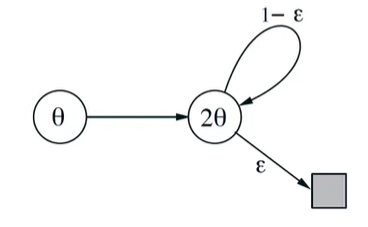
θk+1=arg min⁡θk+1∑s(vθk+1(s)−T∗vk(s))2\theta_{k+1} = \argmin\limits_{\theta_{k+1}}\sum\limits_s(v_{\theta_{k+1}}(s) - T^* v_k(s))^2

이 방법은 위와 같은 문제에서 충분히 발산할 수 있다.

그러나 희망이 없는 편은 아니다.

  • 이 알고리즘의 Sample 버전에서는 웬만한 환경에서 수렴할 수 있다.
  • 심지어 function approximation에서도 발산의 이론적 위험은 실제로는 굉장히 드물게 발생한다.
profile
Bard
돈 되는 건 다 공부합니다.
이전 포스트

C. 마르코프 결정 과정과 DP

다음 포스트

E. Model-free 예측

0개의 댓글