E. Model-free 예측

Bard·2023년 12월 30일
AIRL

Reinforcement Learning

목록 보기
5/10
post-thumbnail

Monte Carlo Algorithms

우리는 모델에 대한 정보 없이 학습하기 위하여 샘플을 사용할 수 있다.

이 방법을 몬테 카를로라고 부르며, 이는 MDP에 대한 지식이 필요 없는 model-free 알고리즘이다.

Monte Carlo: Bandits

간단한 예제로 Multi-armed Bandit을 생각해보자.

각 action에 대하여 reward sample의 평균은 다음과 같다.

qt(a)=∑i=0tI(Ai=a)Ri+1∑i=0tI(Ai=a)≈E[Rt+1∣At=a]q_t(a) = \frac{\sum^t_{i=0}\mathcal{I}(A_i=a)R_{i+1}}{\sum^t_{i=0}\mathcal{I}(A_i=a)} \approx \Bbb{E}[R_{t+1} | A_t = a]

이는 다음과 같다.

qt(At)=qt(At)+1Nt(At)(Rt+1−qt(At))  qt+1(a)=qt(a),∀a≠Atq_t(A_t) = q_t(A_t) + \frac 1 {N_t(A_t)} (R_{t+1} - q_t(A_t)) \\\;\\ q_{t+1}(a) = q_t(a), \forall a \not= A_t

Monte Carlo: Bandits with States

이는 bandit 들을 각각 다른 상태로 생각한다.

  • episode는 아직 한 스텝으로 계산하며
  • action은 state 변화에 영향을 끼치지 않는다.

그러면 우리는 다음을 계산하면 된다.

q(s,a)=E[Rt+1∣St=s,At=a]q(s,a) = \Bbb{E}[R_{t+1} | S_t=s, A_t = a]

이런 bandit을 contextual bandits라고 부른다.

Introduction Function Approximation

Value Function Approximation

우리는 지금까지 거의 룩업 테이블을 고려해왔다.

  • 모든 상태 ss는 v(s)v(s) 엔트리를 가진다.
  • 또는 모든 상태-액션 페어 s,as, a가 q(s,a)q(s,a)를 갖는다.

그런데 이러면 커다란 MDP에서는 이런 문제들이 생긴다.

  • 메모리 상에 저장해야할 상태나 액션들이 너무 많아진다.
  • 그리고 각각의 상태에 대한 value를 개별적으로 학습하는 것이 너무 느리다.
  • 각각의 상태는 보통 fully observable이 아니다.

그래서 해결법을 제시한다.

  • function approximation을 통하여 value function을 추정한다.
    vw(s)≈vπ(s)        or  v∗(s) qw(s,a)≈qπ(s,a)or  q∗(s,a)v_w(s) \approx v_\pi (s)\qquad\qquad\;\;\;\; \text{or}\;v_*(s)\\\ q_w(s,a) \approx q_\pi(s,a)\qquad\qquad \text{or}\;q_*(s,a)
  • Monte Carlo 나 Temporal-Difference 학습을 이용하여 매개변수 w\textbf{w}를 업데이트 한다.
  • 보이지 않는 상태에 대해서도 일반화한다.

Agent state update

큰 MDP에 대하여 환경이 fully observable이 아니라고 가정하자.

이때 다음과 같이 agent state를 정의하자. (w∈Rnw \in \Bbb{R}^n)

St=uw(St−1,At−1,Ot)S_t = u_w(S_{t-1},A_{t-1},O_t)

이제부터 StS_t는 agent state를 의미한다.
이를 우리는 agent 내부의 vector 또는 간단한 케이스에서는 단순히 현재 관측값이라고 볼 수 있다. St=OtS_t = O_t

여기서는 어떻게 agent state update를 학습할 지에 대해선 얘기하지 않을 것이다.

Linear Function Approximation

Feature vectors

다음과 같이 feature vector를 이용하여 상태를 표현해보자.

x(s)=(x1(s)⋮xm(s))\textbf{x}(s) = \begin{pmatrix} x_1(s) \\ \vdots \\ x_m(s) \end{pmatrix}

x:S→Rm\textbf{x} : \mathcal{S} \rarr \Bbb{R}^m은 agent state에서 feature로의 고정된 매핑이며, 간략하게는 xt=x(St)\textbf{x}_t = \textbf{x}(S_t)라고 쓸 수 있다.

예를 들면 이런 곳에 적용할 수 있다.

  • 랜드마크로부터의 로봇의 거리
  • 주식시장에서의 경향
  • 체스에서 기물들과 폰의 배치

Linear Function Approximation

value function을 feature들의 선형 결합을 통해 근사한다.

vw(s)=wTx(s)=∑j=1nxj(s)wjv_\textbf{w}(s) = \textbf{w}^T\textbf{x}(s) = \displaystyle\sum^n_{j=1}x_j(s)w_j

여기에서 loss는 w에 대한 이차식으로 나타난다.

L(w)=ES∼d[(vπ(S)−wTx(S))2]L(\textbf{w}) = \Bbb{E}_{S \sim d} [(v_\pi(S)-\textbf{w}^T\textbf{x}(S))^2]

여기세서 stochastic gradient descent를 사용하면 global optimum으로 수렴하게 되며, 업데이트 수식은 간단하다.

∇wvw(St)=x(St)=xt⇒Δw=α(vπ(St)−vw(St))xt\nabla_\textbf{w}v_\textbf{w}(S_t) = \textbf{x}(S_t) = \textbf{x}_t \Rarr \Delta\textbf{w} = \alpha(v_\pi(S_t) - v_\textbf{w}(S_t))\textbf{x}_t

즉 업데이트는 step-size와 prediction error, feature vector를 곱한 값으로 이루어진다.

Table Lookup Features

Table Lookup은 linear value function approximation의 특별한 케이스다.

nn 상태들이 S={s1,⋯ ,sn}\mathcal{S} = \{s_1, \cdots, s_n\}으로 주어진다고 하자.

이때 다음과 같은 one-hot feature를 사용하자. 여기서 one-hot은 해당하는 값을 제외한 모든 값은 0이 되는 벡터를 의미한다.

x(s)=(I(s=s1)⋮I(s=sn))\textbf{x}(s) = \begin{pmatrix}\mathcal{I}(s = s_1)\\\vdots\\\mathcal{I}(s = s_n)\end{pmatrix}

parameter w\textbf{w}는 오직 각 상태에 대한 value 추정값만을 들고 있게 된다.

v(s)=wTx(s)=∑jwjxj(s)=wsv(s) = \textbf{w}^T\textbf{x}(s) = \sum\limits_j w_j x_j(s) = w_s

Monte Carlo Algorithms

Bandits with States

다시 앞으로 돌아와서 살펴보자. qq는 neural network와 같은 매개변수 함수가 될 것이며, 우리는 loss를 다음과 같이 나타낼 수 있다.

L(w)=12E[(Rt+1−qw(St,At))2]L(\textbf{w}) = \frac 1 2 \Bbb{E}[(R_{t+1} - q_\textbf{w}(S_t,A_t))^2]

그러면 gradient update는 다음과 같을 것이다.

wt+1=wt−α∇wtL(wt)    =wt−α∇wt12E[(Rt+1−qw(St,At))2]              =wt+αE[(Rt+1−qw(St,At))∇wtqwt(St,At)]\textbf{w}_{t+1} = \textbf{w}_t - \alpha\nabla_{\textbf{w}_t}L(\textbf{w}_t) \qquad\qquad\qquad\qquad\\\;\\\qquad\; = \textbf{w}_t -\alpha\nabla_{\textbf{w}_t}\frac 1 2 \Bbb{E}[(R_{t+1} - q_\textbf{w}(S_t,A_t))^2] \\\;\\\qquad\qquad\;\;\;\;\;\; = \textbf{w}_t + \alpha\Bbb{E}\left[(R_{t+1} - q_\textbf{w}(S_t,A_t))\nabla_{\textbf{w}_t}q_{\textbf{w}_t}(S_t,A_t)\right]

여기서 우리는 Stochastic Gradient Update를 얻기 위해 샘플을 사용할 수 있다.

이건 그저 회귀일 뿐이므로 커다란 상태 공간에서도 잘 작동한다.

linear function q(s,a)=wTx(s,a)q(s,a) = \textbf{w}^T\textbf{x}(s,a)를 사용하면,

∇wtqwt(St,At)=x(s,a)\nabla_{\textbf{w}_t}q_{\textbf{w}_t}(S_t,A_t) = \textbf{x}(s,a)

가 될 것이며, 이때 SGD update는 다음과 같을 것이다.

wt+1=wt+α(Rt+1−qw(St,At))x(s,a)\textbf{w}_{t+1} = \textbf{w}_t + \alpha(R_{t+1} - q_\textbf{w}(S_t,A_t))\textbf{x}(s,a)
  • Linear update에서는 step-size ×\times prediction error ×\times feature vector
  • Non-Linear update에서는 step-size ×\times prediction error ×\times gradient

가 되는 것이다.

Monte-Carlo Policy Evaluation

이제 우리는 순차적 결정 문제를 고려할 수 있다.

목표: 정책 π\pi에 의한 경험들로부터 vπv_\pi를 학습하기

S1,A1,R2,⋯ ,Sk∼πS_1,A_1,R_2, \cdots, S_k \sim \pi

return은 전체 discounted reward이다. (T>tT > t에 대하여):

Gt=Rt+1+γRt+2+⋯+γT−t−1RTG_t = R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{T-t-1}R_T

이때 value function은 return의 기댓값이다.

vπ(s)=E[Gt∣St=s,π]v_\pi (s) = \Bbb{E}[G_t|S_t = s,\pi]

우리느 간단히 표본평균을 모평균 대신 사용할 수 있으며, 이를 우리는 Monte-Carlo Policy Evaluation이라고 부른다.

Example: Blackjack

  1. States
  • 현재 총합 (12 ~ 21)
  • 딜러가 보여주고 있는 카드 (ace ~ 10)
  • 내가 사용할 수 있는 ace를 갖고 있는가? (yes or no)
  1. Action
  • stick: 카드 받기를 멈춘다.
  • draw: 다른 카드를 한장 뽑는다. (비복원)
  1. Stick에 대한 Reward
  • 카드의 합이 딜러 카드의 합보다 크면 +1
  • 카드의 합이 딜러 카드의 합과 같으면 0
  • 카드의 합이 딜러 카드의 합보다 작으면 -1
  1. Draw에 대한 Reward
  • 카드의 합이 21보다 커지면 -1 (그리고 종료)
  • 나머지 경우에는 0
  1. 카드의 합이 12보다 작다면 자동 Draw

이 예제에서 MC Approximation을 사용하여 학습을 시키면 상태별로 아래와 같은 결과를 얻을 수 있다.

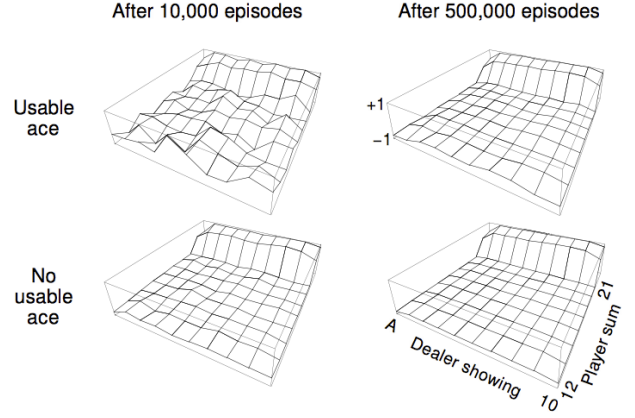
Monte-Carlo Learning의 단점

우리는 Value prediction을 학습하기 위해 사용할 수 있는 MC algorithm들을 봐왔다.

그러나 에피소드 자체가 길어지면, 학습이 느릴 수도 있다.

  • 학습을 시작하기 전에 일단 그 에피소드가 끝나야 한다.
  • 또한 return이 높은 분산을 가질 수 있다.

이에 대한 대안을 소개한다.

Temporal-Difference Learning

Sampling Bellman Equations

이전 시간에 Bellman equation과 iterating을 통한 근사법에 대하여 배웠었다.

vπ(s)=E[Rt+1+γvπ(St+1)∣St=s,At∼π(St)]  vk+1(s)=E[Rt+1+γvk(St+1)∣St=s,At∼π(St)]v_\pi(s) = \Bbb{E}[R_{t+1}+\gamma v_\pi(S_{t+1}) | S_t = s, A_t \sim \pi(S_t)]\\\;\\ v_{k+1}(s) = \Bbb{E}[R_{t+1}+\gamma v_k(S_{t+1}) | S_t = s, A_t \sim \pi(S_t)]

이걸 우리는 아래처럼 표본화할 수 있다!

vt+1(St)=Rt+1+γvt(St+1)v_{t+1}(S_t) = R_{t+1}+\gamma v_t(S_{t+1})

이건 꽤 노이즈가 클 것 같다. 이를 위해 파라미터 α\alpha를 통하여 스텝을 작게 만들 수 있다.

vt+1(St)=vt(St)+αt(Rt+1+γvt(St+1)⏟target−vt(St))v_{t+1}(S_t) = v_t(S_t) + \alpha_t \left(\underbrace{R_{t+1} + \gamma v_t(S_{t+1})}_{\text{target}}-v_t(S_t)\right)

Temporal difference learning

Prediction setting: policy π\pi 하에 이뤄진 경험을 통하여 vπv_\pi를 온라인 학습

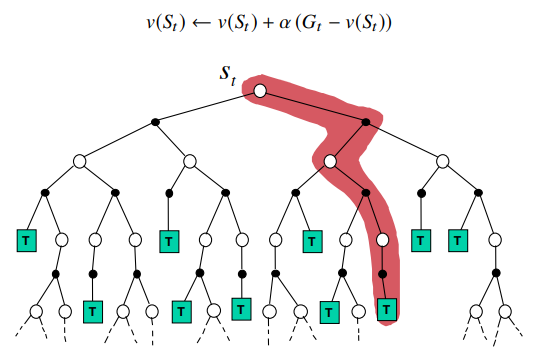
  1. Monte-Carlo
    vn(St)v_n(S_t)를 표본 return GtG_t를 통해 업데이트 함.
    vn+1(St)=vn(St)+α(Gt−vn(St))v_{n+1}(S_t) = v_n(S_t)+\alpha(G_t-v_n(S_t))
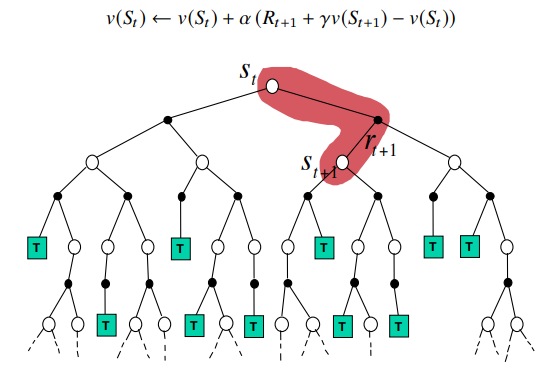
  2. Temporal-difference learning
    vt(St)v_t(S_t)를 추정 return인 Rt+1+γv(St+1)R_{t+1} + \gamma v(S_{t+1})를 통해 업데이트 함
    vt+1(St)=vt(St)+αt(Rt+1+γvt(St+1)⏟target−vt(St)⏞TD error)v_{t+1}(S_t) = v_t(S_t) + \alpha_t \left(\overbrace{\underbrace{R_{t+1} + \gamma v_t(S_{t+1})}_{\text{target}}-v_t(S_t)}^{\text{TD error}}\right)
    δt=Rt+1+γvt(St+1)−vt(St)\delta_t = R_{t+1} + \gamma v_t(S_{t+1})-v_t(S_t)를 TD error라고 부른다.

Summary: DP,MC,TD Backup

Dynamic Programming Backup

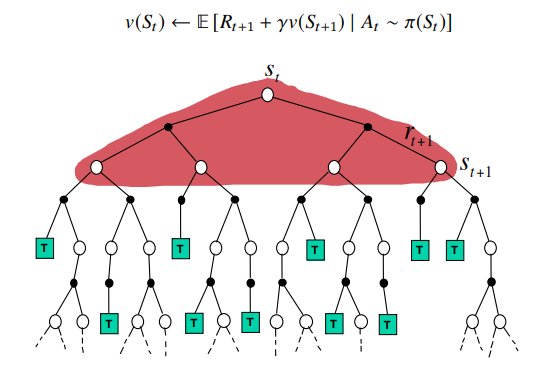
Monte-Carlo Backup

Temporal-Difference Backup

Bootstrapping and Sampling

  1. Bootstraping: 업데이트가 estimate를 필요로 함
  • MC: does not bootstrap
  • DP: bootstraps
  • TD: bootstraps
  1. Sampling: 표본 기댓값을 통해 업데이트함
  • MC: samples
  • DP: does not sample
  • TD: samples

Again: Temporal difference learning

우리는 같은 아이디어를 action value에도 적용할 수 있다.

  • qt(St,At)q_t(S_t, A_t)를 추정 return인 Rt+1+γq(St+1,At+1)R_{t+1} + \gamma q(S_{t+1},A_{t+1})를 통해 업데이트 함
    qt+1(St,At)=qt(St,At)+αt(Rt+1+γqt(St+1,At+1)⏟target−qt(St,At)⏞TD error)q_{t+1}(S_t,A_t) = q_t(S_t,A_t) + \alpha_t \left(\overbrace{\underbrace{R_{t+1} + \gamma q_t(S_{t+1}, A_{t+1})}_{\text{target}}-q_t(S_t,A_t)}^{\text{TD error}}\right)

이 알고리즘은 SARSA라고도 부르는데, (St,At,Rt+1,St+1,At+1)(S_t,A_t,R_{t+1},S_{t+1},A_{t+1})을 사용하기 때문이다.

TD는 model-free이며, 경험으로부터 직접 학습한다.
TD는 완료되지 않은 episode에 대해서도 bootstrapping을 통해 학습할 수 있으며, 그렇기에 episode가 진행중일때에도 학습할 수 있다.

Comparing MC and TD

MC vs TD

  • TD는 최종 결과를 알기 전에도 학습할 수 있다.
    • TD는 각 step 이후에 online으로 학습할 수 있다.
    • MC는 무조건 return이 나오기 전까지 episode가 끝나는 것을 기다려야 한다.
  • TD는 최종 결과가 없어도 학습할 수 있다.
    • TD는 incomplete sequence를 통해서도 학습할 수 있다.
    • MC는 complete sequence를 통해서만 학습할 수 있다.
    • TD는 끊이지 않는 환경에서도 작동한다.
    • MC는 끊어지는 환경에서만 작동한다.
  • TD는 예측에 걸리는 시간과 독립적이다.
    • TD는 단일 트랜지션에서도 학습할 수 있다.
    • MC는 episode가 끝날때 업데이트하기 위해 모든 예측을 저장하여야 한다.
  • TD는 합리적인 value estimate가 필요하다.

Bias/Variance Trade-off

  • MC의 리턴값 Gt=Rt+1+γRr+2+⋯G_t = R_{t+1} + \gamma R_{r+2} + \cdots는 vπ(St)v_\pi(S_t)의 unbiased 추정값이다.

  • TD의 타겟 Rt+1+γvt(St+1)R_{t+1} + \gamma v_t(S_{t+1})는 vπ(St)v_\pi(S_t)의 biased 추정값이다. (vt(St)=vπ(St)v_t(S_t) = v_\pi(S_t)가 아니라면)

  • 그러나 TD target은 더 낮은 분산을 갖는다.

    • MC return은 많은 랜덤 액션, 트랜지션, 리워드의 영향을 받지만
    • TD target은 하나의 랜덤 액션, 트랜지션, 리워드의 영향을 받는다.

  • 몇몇 상황에서 TD는 비가역적인 bias를 가질 수 있다.

  • partially observable한 상황에서, MC는 암묵적으로 모든 잠재변수를 계산한다.

Example: Random Walk

이런 상황을 가정하자.

  • transition은 왼쪽, 오른쪽 50%로 동일하고, Initial value는 v(s)=0.5,∀sv(s) = 0.5, \forall s라고 하자.
  • 이때 실제 value는 다음과 같이 나타날 것이다.
    v(A)=16,v(B)=26,v(C)=36,v(D)=46,v(E)=56v(A) = \frac 1 6, v(B) = \frac 2 6, v(C) = \frac 3 6, v(D) = \frac 4 6, v(E) = \frac 5 6

이때 TD와 MC에서의 평균 제곱근 오차 (RMSE)는 다음과 같이 나타난다.

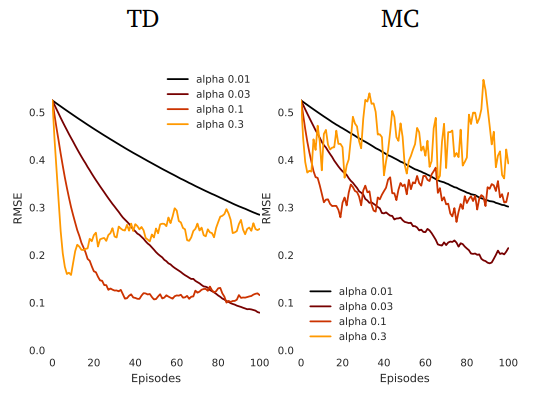
Batch MC and TD

MC와 TD는 experience→∞\text{experience} \rarr \infin, αt→0\alpha_t \rarr 0이라면 vt→vπv_t \rarr v_\pi로 수렴한다.

그러나 만약 경험이 유한하다면 어떨까?

다음과 같이 경험의 fixed batch를 생각해보자.

episode 1: S11,A11,R21,⋯ ,ST11  ⋮  episode K: S1K,A1K,R2K,⋯ ,STKK\text{episode 1: }\qquad S^1_1,A^1_1,R^1_2,\cdots,S^1_{T_1}\\\;\\ \vdots\\\;\\ \text{episode K: }\qquad S^K_1,A^K_1,R^K_2,\cdots,S^K_{T_K}

이때 우리는 k∈[1,K]k \in [1,K] 에피소드에서 반복적으로 표본을 추출하여 MC나 TD(0)에 적용할 수 있다. = 경험적 모델에 의한 표본 추출

Differences in batch solutions

  • MC는 관측된 return을 통해 최고의 mean-squared fit으로 수렴한다.

    ∑k=1K∑t=1TK(Gtk−v(Stk)))2\displaystyle\sum^K_{k=1}\sum^{T_K}_{t=1}\left(G_t^k - v(S_t^k))\right)^2

  • TD는 주어진 데이터를 기반으로 max likelihood 마르코프 모델로 수렴한다.

    • 주어진 데이터가 가장 잘 맞는 경험적 MDP (S,A,p^,γ)(\mathcal{S}, \mathcal{A},\hat{p}, \gamma)를 찾는다.

MC vs TD

  • TD는 Markov property를 이용한다.
    • 이는 fully-observable 환경에서 유용하다.
  • MC는 Markov property를 이용하지 않는다.
    • 이는 partially-observable 환경에서 유용하다.
  • 유한한 데이터 또는 함수 근사를 하게 되면 solution은 달라질 수 있다.

Between MC and TD: Multi-Step TD

Unified View of RL

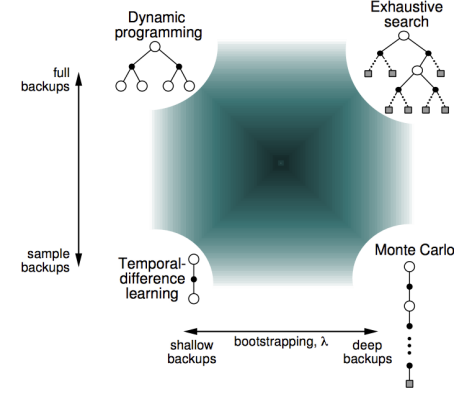
Multi-Step Updates

  • TD는 정확하지 않을 수 있는 value estimate를 사용한다.
  • 추가로 정보가 전파되는 속도가 꽤 느리다.
  • MC는 전파가 빠르지만, update에 더 noise가 많다.
  • 따라서 우리는 TD와 MC 그 중간을 찾고자 한다.

Multi-Step Prediction

TD target이 미래의 nn 스텝을 본다고 해보자.

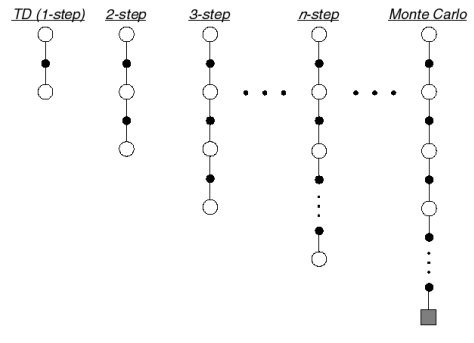
Multi-Step Returns

각 nn-step의 리턴을 n=1,2,⋯ ,∞n=1,2,\cdots,\infin에 대해 생각해보자.

n=1(TD)Gt(1)=Rt+1+γv(St+1)n=2  Gt(2)=Rt+1+γRt+2+γ2v(St+2)⋮⋮n=∞(MC)    Gt(∞)=Rt+1+γRt+1+⋯+γT−t−1RT\begin{matrix} n = 1& \red{(TD)} & {G_t^{(1)} = R_{t+1} + \gamma v(S_{t+1})\qquad\qquad\qquad} \\ n = 2&\qquad &{\;G_t^{(2)} = R_{t+1} + \gamma R_{t+2} + \gamma^2 v(S_{t+2})\qquad} \\ \vdots & & \vdots \\ n = \infin &\red{(MC)}& {\;\;G_t^{(\infin)} = R_{t+1} + \gamma R_{t+1} + \cdots + \gamma^{T-t-1}R_T} \end{matrix}

이때 일반적으로 nn-step은 다음과 같이 정의된다.

Gt(∞)=Rt+1+γRt+1+⋯+γn−1Rt+n+γnv(St+n)G_t^{(\infin)} = R_{t+1} + \gamma R_{t+1} + \cdots + \gamma^{n-1}R_{t+n} + \gamma^n v(S_{t+n})

그리고 Multi-step temporal-difference learning은 다음과 같이 진행한다.

v(St)←v(St)+α(Gt(n)−v(St))v(S_t) \larr v(S_t) + \alpha(G^{(n)}_t-v(S_t))

Grid Example

Large Random Walk Example

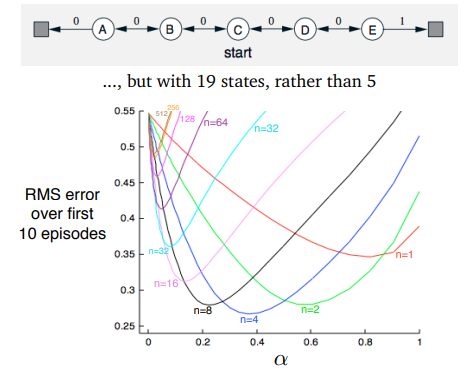
Mixed Multi-Step Returns

여러 state에 대하여 약간의 bootstrap을 수행할 수도 있다.

Gtλ=Rt+1+γ((1−λ)v(St+1)+λGt+1λ)G^\lambda_t = R_{t+1} + \gamma\left((1-\lambda)v(S_{t+1})+\lambda G^\lambda_{t+1}\right)

이 방식은 nn-step return에 대하여 가중치 평균을 제공한다.

Gtλ=∑n=1∞(1−λ)λn−1Gt(n)G^\lambda_t = \displaystyle\sum^\infin_{n=1}(1-\lambda)\lambda^{n-1}G^{(n)}_t

그리고 이는 이렇게 변형할 수 있다.

Gtλ=Rt+1+γ((1−λ)v(St+1)+λGt+1λ)G^\lambda_t = R_{t+1} + \gamma((1-\lambda)v(S_{t+1})+\lambda G^\lambda _{t+1})

λ\lambda가 0인경우 TD, λ\lambda가 1인 경유 MC가 되는 것을 알 수 있다.

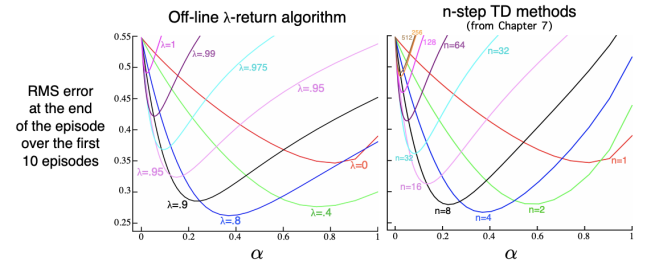
Benefits of Multi-Step Learning

  • Multi-step은 TD와 MC 의 이점을 동시에 가져갈 수 있다.
  • Bootstrapping은 bias와 관련한 문제가 있을 수 있고,
  • Monte Carlo는 variance와 관련한 문제가 있을 수 있다.
  • 전형적으로 nn이나 λ\lambda는 중간정도 값을 골랐을 때 좋다.

Eligibility Traces

Independence of temporal span

MC와 multi-step은 예측하는 시간에 독립적이지 못하다. 긴 episode에서 value를 업데이트하기 위해서는 기다려야만 한다.

반면 TD는 즉시 업데이트할 수 있고, 예측 시간으로부터 독립적이다.

어떻게하면 두 마리 토끼를 다 잡을 수 있을까?

Eligibility traces

다시 linear function approximation을 가져와보자.

vw(s)=wTx(s)v_\textbf{w}(s) = \textbf{w}^T\textbf{x}(s)에 대한 Monte Carlo와 TD 업데이트는 다음과 같다.

Δwt=α(Gt−v(St))xt            (MC)Δwt=α(Rt+1+γv(St+1)−v(St))xt(TD)\Delta \textbf{w}_t = \alpha(G_t-v(S_t))\textbf{x}_t\qquad\qquad\qquad\;\;\;\;\;\;\text{(MC)}\\ \Delta \textbf{w}_t = \alpha(R_{t+1}+ \gamma v(S_{t+1})-v(S_t))\textbf{x}_t\qquad\text{(TD)}

episode kk에서 MC는 모든 상태들을 한번에 업데이트한다.

Δwk+1=∑t=0T−1α(Gt−v(St))xt\Delta\textbf{w}_{k+1} = \displaystyle\sum^{T-1}_{t=0}\alpha(G_t-v(S_t))\textbf{x}_t

모든 업데이트를 누적하면 다음과 같다:

Δwt≡αδtetwhere  et=γλet−1+xt\Delta\textbf{w}_t \equiv \alpha\delta_t e_t\\ \text{where}\quad\; e_t = \gamma\lambda e_{t-1} + x_t

여기서 우리는 다음의 직관을 얻을 수 있다: 현재 TD error에 대한 과거 상태의 자격을 축소하고, 더해준다.

이건 꽤나 신기한데, 우리는 이제 모든 과거 상태들을 한번의 업데이트만으로 업데이트할 수 있다. 더이상 각각을 다시 계산할 필요가 없다.

이 아이디어는 function approximation으로 확장된다.

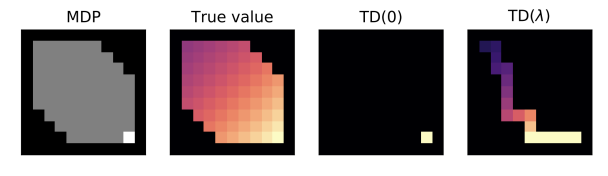
우리는 MC error를 TD error들의 합으로 다시 쓸 수 있다.

Gt−v(St)=Rt+1+γGt+1−v(St)      =Rt+1+γv(St+1)−v(St)⏟=δt+γ(Gt+1−v(St+1))=δt+γ(Gt+1−v(St+1))            =⋯=δt+γδt+1+γ2(Gt+2−v(St+2))            =⋯      =∑k=tTγk−tδkG_t - v(S_t) = R_{t+1} + \gamma G_{t+1} - v(S_t)\qquad\qquad\qquad\qquad\qquad\qquad\;\;\;\\ \qquad= \underbrace{ R_{t+1} + \gamma v(S_{t+1}) - v(S_t)}_{=\delta_t}+\gamma(G_{t+1}-v(S_{t+1}))\\ = \delta_t + \gamma(G_{t+1}-v(S_{t+1}))\qquad\qquad\qquad\;\;\;\;\;\;\\ =\cdots\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\\ =\delta_t + \gamma\delta_{t+1} + \gamma^2(G_{t+2}-v(S_{t+2}))\qquad\;\;\;\;\;\;\\ =\cdots\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\;\;\;\\ = \displaystyle\sum^T_{k=t}\gamma^{k-t}\delta_k\qquad\qquad\qquad\qquad\qquad\qquad\quad

이제 전체 에피소드에 대한 누적을 고려하면 다음과 같아진다.

Δwk=∑t=0T−1α(Gt−v(St))xt          =∑t=0T−1α(∑k=tTγk−tδk)xt=∑k=0T−1α∑t=0kγk−tδkxt            =∑k=0T−1αδk∑t=0kγk−txt⏟≡ek            =∑k=0T−1αδkek=∑t=0T−1αδtet\Delta \textbf{w}_k = \displaystyle\sum^{T-1}_{t=0}\alpha(G_t-v(S_t))x_t\qquad\;\;\;\;\;\\ = \sum^{T-1}_{t=0}\alpha\left(\sum^T_{k=t}\gamma^{k-t}\delta_k \right) x_t\\ = \sum^{T-1}_{k=0}\alpha\sum^k_{t=0}\gamma^{k-t}\delta_kx_t\;\;\;\;\;\;\\ =\sum^{T-1}_{k=0}\alpha\delta_k\underbrace{\sum^k_{t=0}\gamma^{k-t}x_t}_{\equiv e_k}\;\;\;\;\;\;\\ = \sum^{T-1}_{k=0}\alpha\delta_ke_k = \sum^{T-1}_{t=0}\alpha\delta_te_t

여기서

et=γet−1+xte_t = \gamma e_{t-1} + x_t

가 되는데, 이 ete_t를 eligibility trace라고 부르며, 각 스텝마다 이는 γ\gamma에 따라 작아지고, 현재 feature xtx_t가 더해진다.

Intuition: 같은 TD error가 여러 MC error들에서 나타나므로, 이를 grouping하면 모든 과거 상태들을 한번의 업데이트만에 적용할 수 있다.

Mixed Multi-Step Returns and Eligibility Traces

다시 mixed multi-step return을 가져와보자.

Gtλ=Rt+1+γ((1−λ)v(St+1)+λGt+1λ)G^\lambda_t = R_{t+1} + \gamma((1-\lambda)v(S_{t+1})+\lambda G^\lambda _{t+1})

여기서 연관된 에러와 trace update는

Gtλ=∑k=0T−tλkγkδt+kG^\lambda_t = \sum^{T-t}_{k=0}\lambda^k \gamma^k \delta_{t+k}

이며, 여기서

et=γλet−1+xtandΔw+t=αδtete_t = \gamma\lambda e_{t-1} + x_t\quad\text{and}\quad\Delta\textbf{w}+t = \alpha\delta_t e_t

가 된다.

이를 decay γλ\gamma\lambda인 accumulating trace라고 부른다.

이는 batched episodic update(offline)에 대한 것이고, online updating에 대해서도 비슷한 trace가 존재한다.

profile
Bard
돈 되는 건 다 공부합니다.
이전 포스트

D. DP의 이론적 기초

다음 포스트

[RL] Reinforcement Learning Overview

0개의 댓글