Introduction

R1. Guarantee of timely execution , R2. High tracking accuracy

No study has achieved both for multiple MOT tasks to be applied to a vision system with multiple cameras.

Key questions addressed

• How can we design the system architecture of RT-MOT to provide a control knob to explore a trade-off between R1 and R2?
• How can we efficiently utilize the proposed system architecture to achieve R1 and R2?

---

Contributions

• Motivate the importance of choosing a proper pair of detection and association models to explore a trade-off between R1 and R2.
• Propose the first system design RT-MOT, which addresses R1 and R2 for multiple MOT tasks.
• Re-define and estimate a measure, which enables to predict tracking accuracy variation to be used in the scheduling framework.
• Develop a novel confidence-aware real-time scheduling framework for RT-MOT, which offers both offline and online timing guarantees with flexible execution
• Demonstrate the effectiveness of RT-MOT through experiment on an actual computing system.

Target System: DNN-based Multi-Object Tracking

Trade-off between Execution Time and Tracking Accuracy

Experiment inputs

• High-confidence detection ($D^H$) : processing a full-size frame
• Low-confidence detection ($D^L$) : processing a partial portion of a frame
• High-confidence association ($A^H$) : performing both feature- and IoU-based methods
• Low-confidence association ($A^L$) : performing the IoU-based method only

Observations

• There exists a trade-off between execution time and tracking accuracy in choosing the ratio of high-confidence detection/association.
• Tracking accuracy varies greatly with different combinations of a choice of detection and association schemes, although the combinations yield similar computation time.

Challenges

• There exists a huge number of possible combinations of the choices of detection and association schemes for a frame sequence.
• The tracking accuracy of one combination also dynamically varies with the input frame sequence.
• + Multiple tasks

System Goal and Overview

RT-MOT

• Supports dynamic selection of different execution models for detection and association.
• Run-time frame-level scheduling decisions

Key issues

• I1) How to estimate the variation of overall accuracy according to different detector/tracker selections of the next frame?
• I2) How to provide an offline timing guarantee to multiple MOT tasks while maximizing the overall accuracy at runtime using the answer of I1?
• I3) How to design the system architecture that supports flexible tracking-by-detection and provides an interface that can accommodate the answer of I1 and I2?

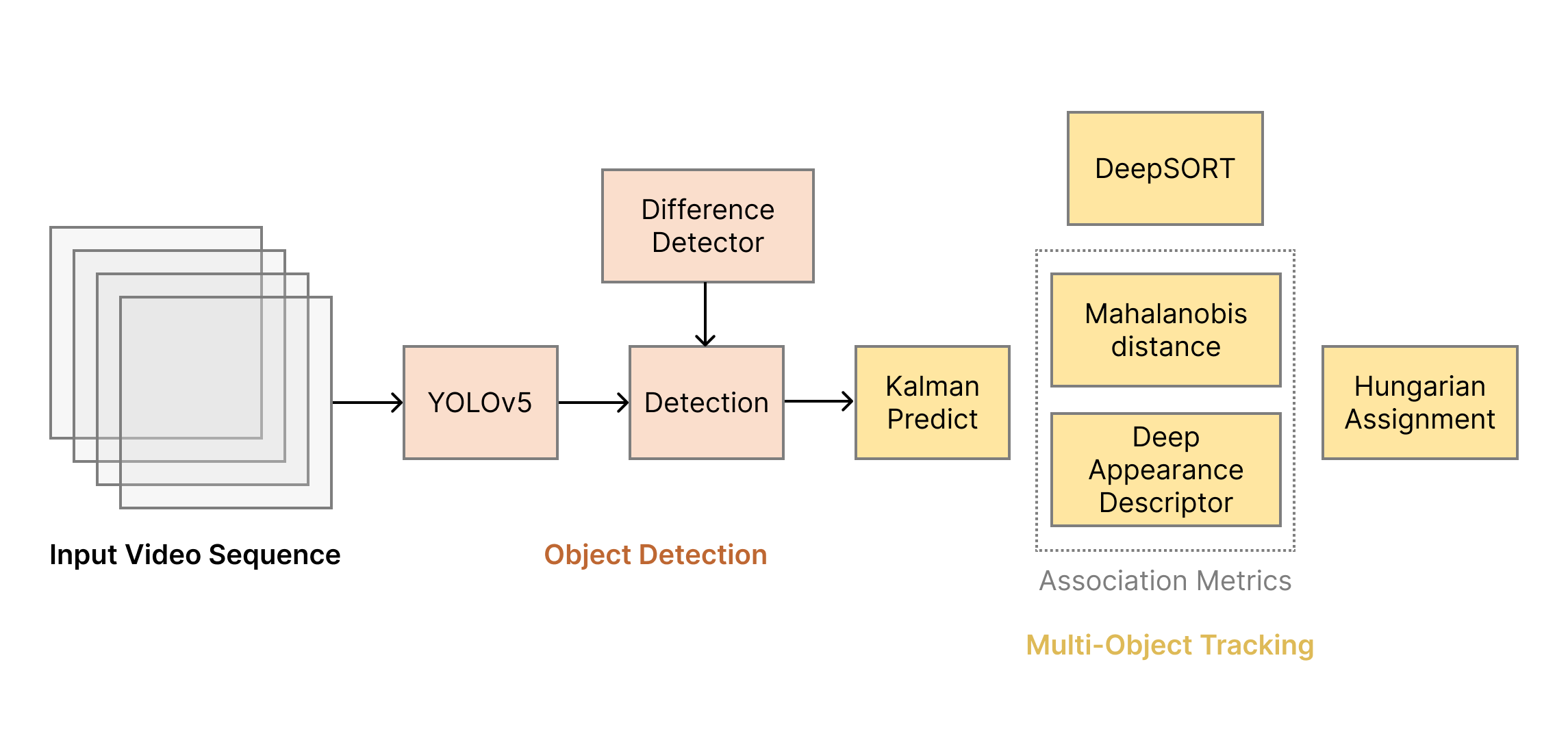
Design of RT-MOT

1. Dynamic tracking-by-detection execution pipeline

• High-confidence detector ($D^H$) : process a full-size frame (672 $\times$ 672)
• Low-confidence detection ($D^L$) : process a RoI of a frame (256 $\times$ 256)
• High-confidence association ($A^H$) : feature-based + IoU-based
• Low-confidence association ($A^L$) : IoU-based only

2. Multi-object tracking confidence estimator

• Tracklet confidence: $\Omega(\chi^t_i) = \Omega_M (M^t_i) \times \Omega_A (A^t_i)$
• Motion confidence($\Omega_M(M^t_i)$): specified as position, size, and velocity.
• Appearance confidence($\Omega_A(A^t_i)$): feature vector extracted by feature extractor.

3. Frame-level flexible scheduler

• The scheduler determines each frame’s priority and its pair of detector and tracker according to non-preemptive fixed-priority with the minimum execution by default.
• Considering the currently available running time, prioritize and select detection and association models that provide higher accuracy.

Tracking confidence

Definition of Tracklet

Object, $O^t_i$

• the $i$-th object response detected at the $t$-th frame
• $O^t_i = (M^t_i, A^t_i)$ : motion state, appearance state

Tracklet, $\chi^t_i$

• a set of tracks followed by $O^t_i$ up to the $t$-th frame
• $\chi^t_i = \{ O^k_i \mid t_s^i \leq k \leq t_e^i \leq t \}$

Tracklets set, $\Phi_{1:t}$

• A set of tracklets of all objects up to the $t$-th frame.

Tracklet confidence definition

Tracklet confidence, $\Omega(\chi^t_i)$

• $\Omega(\chi^t_i) = \Omega_M (M^t_i) \times \Omega_A (A^t_i)$

Motion confidence, $\Omega_M(M^t_i)$

• specified as position, size, and velocity.

Appearance confidence, $\Omega_A(A^t_i)$

• feature vector extracted by feature extractor.

Updating tracklet confidence

CG1. $χ^t_i$ is matched with one of the detected objects by high-confidence association.

CG2. $χ^t_i$ is matched with one of the detected objects by low-confidence association.

CG3. $χ^t_i$ is unmatched with any of the detected objects.

Calculating variation of confidences

1. Motion confidence variation ($\Delta M^{t-1}_i$)

   $\Delta M^{t-1}\_i = \Lambda_s(M^{t-f}\_i, M^{t-1}\_i) \times \Lambda_v(M^{t-f}\_i, M^{t-1}\_i) \tag{2}$

   where

   $\Lambda_s(M^{t-f}_i, M^{t-1}_i) = -\frac{1}{4} \left( \frac{h^{t-f}_i - h^{t-1}_i}{h^{t-f}_i + h^{t-1}_i} + \frac{w^{t-f}_i - w^{t-1}_i}{w^{t-f}_i + w^{t-1}_i} \right) + \frac{1}{2} \tag{3}$
   $\Lambda_v(M^{t-f}_i, M^{t-1}_i) = 1 - 2 \left| \sigma \left( \frac{vx^{t-f}_i - vx^{t-1}_i}{vx^{t-f}_i + vx^{t-1}_i} + \frac{vy^{t-f}_i - vy^{t-1}_i}{vy^{t-f}_i + vy^{t-1}_i} \right) - \frac{1}{2} \right| \tag{4}$

2. Appearance confidence variation ($\Delta A^{t-1}_i$)

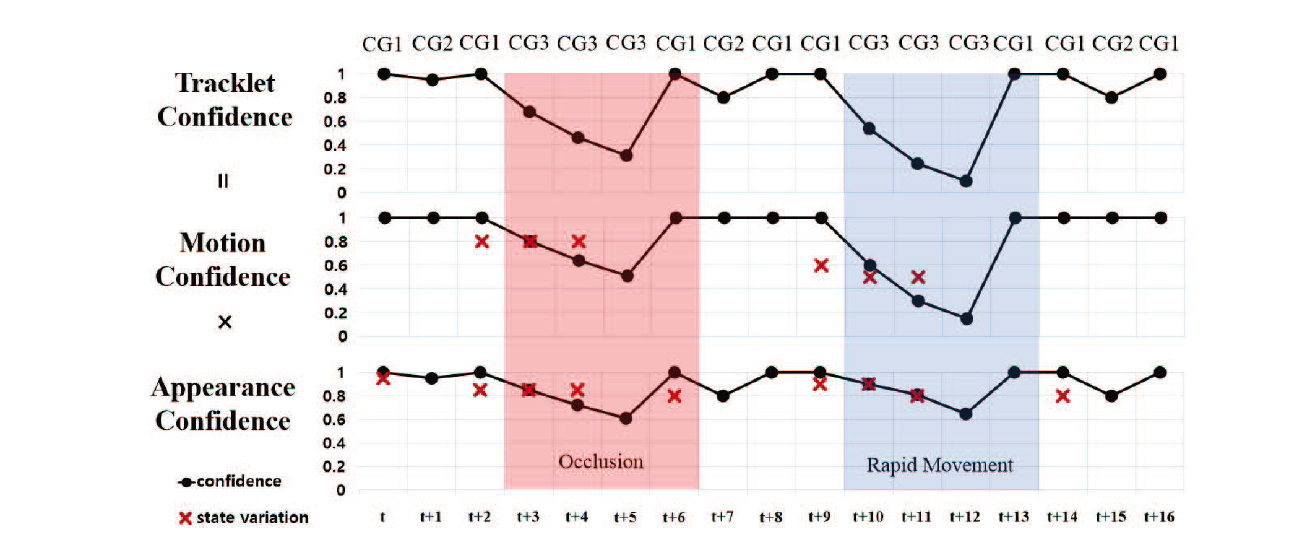
Tracklet Confidence Prediction for next frame

Confidence Prediction Model

1. ($D_H$, $A_H$) : all tracklets belong to CG1.
2. ($D_L$, $A_H$) : a subset of tracklets in RoI belongs to CG1, and the rest of tracklets outside RoI belongs to CG3.
3. ($D_H$, $A_L$) : all tracklets belong to CG2.
4. ($D_L$, $A_L$) : a subset of tracklets in RoI belongs to CG2, and the rest of tracklets outside RoI belongs to CG3.

Expected Confidence Score Calculation

Measured Confidence Score Calculation

Confidence Improvement Calculation

Scheduling Framework for RT-MOT

Scheduling Framework, NPFP$^\textrm{flex}$

1. First, NPFP$^\textrm{flex}$ shares the existing offline schedulability test for NPFP$^\textrm{min}$, which offers timely execution of every instance (i.e. job) of a set of multi-object tracking tasks.

2. Second, NPFP$^\textrm{flex}$ checks the feasibility for each active job to be executed beyond its minimum execution requirement, without compromising the schedulability of any future jobs to executed according to NPFP$^\textrm{min}$.

3. Third, NPFP$^\textrm{flex}$ chooses to execute the job that yields the largest expected improvement of confidence score

Task Model

Periodic task model

• $\tau_i = (T_i, C_i)$
• $C_i = C_i^D + C_i^A$ (detection + association)

Detection part

• $c^{pre}$: the WCET for RoI identification and image cropping.
• $c^{inter}(L \text{ or } H)$: the total inference time for YOLOv5 that has the two different WCETs for low-confidence ($L$) and high-confidence ($H$) detection.
• $C^D_i(L \text{ or } H) = c^{pre} + c^{infer}_i (L \text{ or } H)$

Association part

• $c_i^{as}(L \text{ or } H)$: the WCET for low-confidence (L) and high-confidence (H) association.
• $c_i^{IoU}$: the WCET for a simple IoU-based matching algorithm.
• $c_i^{cascade}$: the WCET for feature-based method.
• $c_i^{as}(H) = c_i^{IoU} + c_i^{cascade}$, $c_i^{as}(L) = c_i^{IoU}$
• $c^{post}$: the WCET for updating the confidence of all tracklets in each task.
• $C^A_i(L \text{ or } H) = c^{as}_i (L \text{ or } H) + c^{post}$

Combinations

• $\{ C^{LL}_i, C^{LH}_i, C^{HL}_i, C^{HH}_i \}$

Base Scheduling Algorithm

NPFP$^\textrm{min}$

Same as the traditional non-preemptive fixed-priority scheduling with $C_i = C^{LL}_i$ for every $τ_i ∈ τ$.

Lemma 1
Suppose that a task set $τ$ is scheduled by the NPFP$^\textrm{min}$ scheduling algorithm.
If every task $τ_i ∈ τ$ satisfies $Eq. (9)$, every job invoked by tasks in $τ$ cannot miss its deadline.

$R_i ≤ T_i, \tag{9}$

where $R_i$, the worst-case response time of $τ_i$, is calculated by finding $R_i(x + 1) = R_i(x)$ through iteration from $R_i(0) = C^{LL}_i + max_{τ_j} ∈ LP(τ_i)C^{LL}_j$ in $Eq. (10)$.

$R_i(x+1) = C^{LL}_i + \max_{\tau_j \in LP(\tau_i)} C^{LL}_j + \sum_{\tau_h \in HP(\tau_i)} \left\lceil \frac{R_i(x)}{T_h} \right\rceil \cdot C^{LL}_h \tag{10}$

Novel Scheduling Framework for RT-MOT

NPFP$^\textrm{flex}$

To guarantee the feasibility of a job, we need to guarantee

• No deadline miss of $J_k$ if it starts its execution for $C_k$ at $t_0$.
• No deadline miss of all future jobs to be executed after $J_k$ according to NPFP$^\textrm{min}$.

If it's deemed feasible to execute $J_k$ for given $C_k$,

• we calculate $\Delta\bar{\Omega}_{τ_k}$
• set $flex$ to T.

If flex is T, find the largest $\Delta\bar{\Omega}_{τ_k}$

otherwise, follow NPFP$^\textrm{min}$.

Online feasibility test

• $Z_i(t)$: the existence of an active job of $τ_i$ at $t$.
• $r_i(t)$: the earliest release time of any job of $τ_i$ after or at $t$.
  (if $Z_i(t) = T$, then the deadline of a job of $\tau_i$)

Lemma 2
Suppose that we start to execute a job of $τ_k$(denoted by $J_k$) at $t_0$ for at most $C_k$.
Then, if $Eq. (11)$ holds, $J_k$ cannot miss its deadline.

$C_k ≤ r_k(t_0) − t_0 \tag{11}$

Lemma 3

Suppose that
(i) We start to execute an active job of $τ_k$ (denoted by $J_k$) at $t_0$ for at most $C_k$
(ii) All jobs to be executed after $J_k$’s execution are scheduled by NPFP$^\textrm{min}$

If $Eq. (12)$ holds, the earliest job of a given $τ_j$ with $Z_j(t_0) = T$ to be executed after $J_k$’s execution (denoted by $J_j$) cannot miss its deadline. (Note that $τ_j$ can be $τ_k$.)

$\begin{aligned} C^{LL}_j &+ C_k + \sum_{\tau_h \in HP(\tau_j) \setminus \{\tau_k\} | Z_h(t_0) = T} C^{LL}_h \\ &+ \sum_{\tau_h \in HP(\tau_j) | r_h(t_0) < r_j(t_0)} \left\lceil \frac{r_j(t_0) - r_h(t_0)}{T_h} \right\rceil C^{LL}_h \leq r_j(t_0) - t_0 \tag{12} \end{aligned}$

Lemma 4

Suppose that
(i) We start to execute an active job of $τ_k$ (denoted by $J_k$) at $t_0$ for at most $C_k$
(ii) All jobs to be executed after $J_k$’s execution are scheduled by NPFP$^\textrm{min}$
(iii) $Eq. (9)$ holds for every $τ_i ∈ τ$.

If $Eq. (13)$ holds, the earliest job of a given $τ_j$ with $Z_j(t_0) = F$ to be executed after $J_k$’s execution (denoted by $J_j$) cannot miss its deadline. (Note that $τ_j$ cannot be $τ_k$.)

$\begin{aligned} C^{LL}_j &+ C_k + \sum_{\tau_h \in HP(\tau_j) \setminus \{\tau_k\} | Z_h(t_0) = T} C^{LL}_h \\ &+ \sum_{\tau_h \in HP(\tau_j) | r_h(t_0) < r_j(t_0) + T_j} \left\lceil \frac{r_j(t_0)+T_j - r_h(t_0)}{T_h} \right\rceil C^{LL}_h \\\;\\ &\leq r_j(t_0) +T_j - t_0 \tag{13} \end{aligned}$

Lemma 5
Suppose that
(i) a job of $τ_j$ (denoted by $J_j$ ) starts its execution at $t_1$ and does not miss its deadline if it executes for up to $C^{LL}_j$,
(ii) all jobs to be executed after $J_j$ ’s execution are scheduled by NPFP$^\textrm{min}$, and
(iii) $Eq. (9)$ holds for every $τ_i ∈ τ$ .

Then, any job of $τ_j$ to be executed after $J_j$ ’s execution cannot miss its deadline.

Theorem 1
Suppose that a task set $τ$ is scheduled by NPFP$^\textrm{flex}$ in Algorithm 1.
If every task $τ_i ∈ τ$ satisfies $Eq. (9)$, every job invoked by tasks in $τ$ cannot miss its deadline.

Experimental Setup

Hardware and Software

• Intel(R) Xeon(R) Silver 4215R CPU @ 3.20GHz, 251.5GB RAM, NVIDIA V100 GPU.
• Ubuntu 18.04.4 with CUDA 10.2, and PyTorch 1.10.2
• YOLOv5 as a front-end detector.
• Waymo Open dataset.
• DeepSORT, SORT for association.

Experimental Setup

Execution time profiling and run-time overhead

$Time(ms)$	$c^{pre}$	$c^{infer}(L)$	$c^{infer}(H)$	$c^{as}(L)$	$c^{as}(H)$	$c^{post}$
$Average$	0.6	12.6	13.1	3.2	23.4	0.7
$Maximum$	0.9	17.6	23.2	9.6	32.7	0.9

• $c^{pre}$: the WCET for RoI identification and image cropping.
• $c^{inter}(L \text{ or } H)$: the total inference time for YOLOv5 that has the two different WCETs for low-confidence ($L$) and high-confidence ($H$) detection.
• $c_i^{as}(L \text{ or } H)$: the WCET for low-confidence (L) and high-confidence (H) association.
• $c_i^{as}(H) = c_i^{IoU} + c_i^{cascade}$, $c_i^{as}(L) = c_i^{IoU}$
• $c^{post}$: the WCET for updating the confidence of all tracklets in each task.

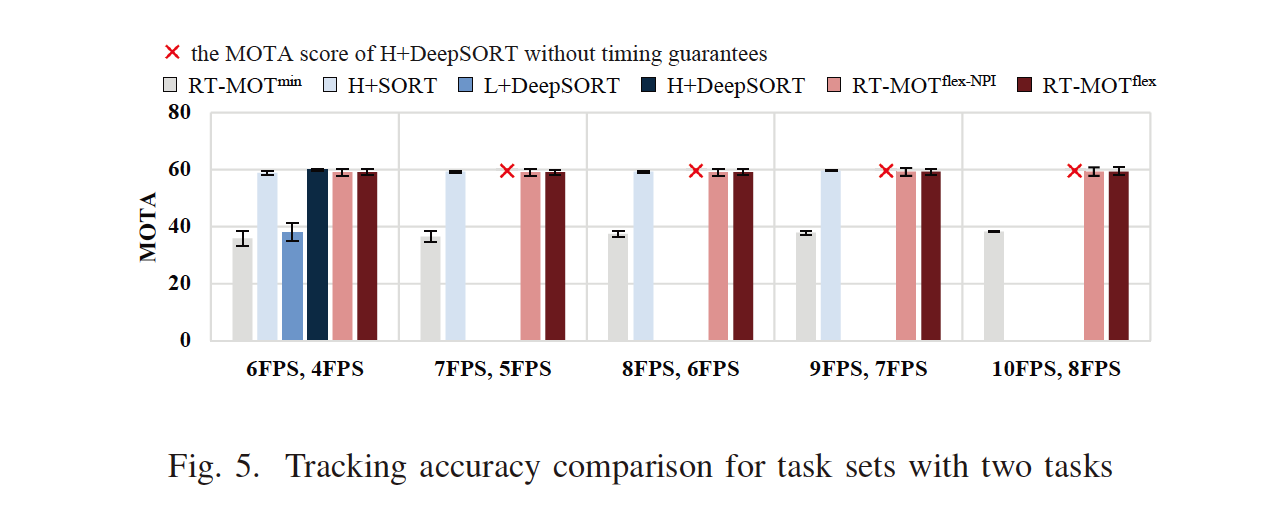
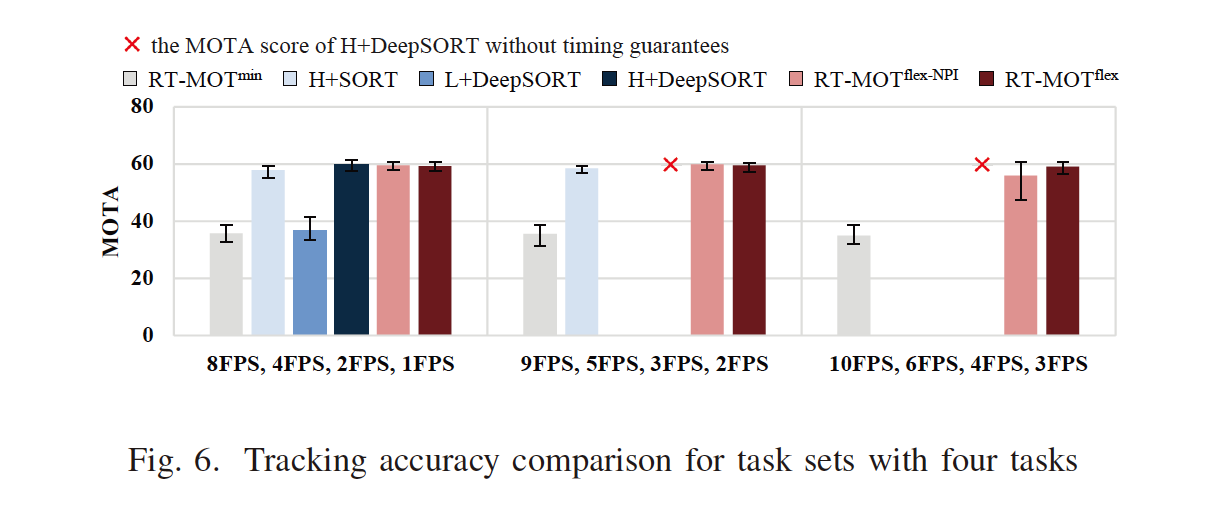
Experimental Results

MOTA

• $g_t$: the number of all objects for time $t$
• $m_t$: the number of missed for time $t$
• $fp_t$: the number of false positive for time $t$
• $mme_t$: the number of mismatches for time $t$

Three versions

• RT-MOT$^\textrm{min}$ employs NPFP$^\textrm{min}$.
• RT-MOT$^\textrm{flex-NPI}$ employs NPFP$^\textrm{flex}$ but does not allow priority inversion.
• RT-MOT$^\textrm{flex}$ employs NPFP$^\textrm{flex} $ in Algorithm 1 as it is.

Fixed-Priority policy

• Rate-monotonic

Popular RT-MOT versions

• H+SORT employs YOLOv5 with the original frame size (672×672) for detection and SORT for association.
• L+DeepSORT employs YOLOv5 with the down-scaled frame size (256×256) for detection and DeepSORT for association.
• H+DeepSORT employs YOLOv5 with the original frame size (672×672) for detection and DeepSORT for association.

Related work

Subject	Related works
One-Stage MOT	FairMOT, ByteTrack
Two-Stage MOT	DeepSORT, StrongSORT
RT Detection	DNN-SAM, AnytimeNet
RT Scheduling	SubFlow, Real-Time Multi-Path
Single MOT Task	Self-cueing Attention

Conclusion

RT-MOT

• a method to estimate the overall accuracy variation according to different detector/tracker selections
• a scheduling framework that provides offline timing guarantees while maximizing overall accuracy at run-time using the method
• a system architecture that supports the framework.

Future Works

• More combinations of various detectors and trackers
• Improve the scheduling framework in terms of schedulability performance.
  (e.g., by allowing a preemption between the completion of detection and the beginning of association for each MOT task.)