Gradient Descent

Gradient descent는 주어진 데이터셋에 대해 손실 함수(Loss)를 최소화하기 위한 최적화 알고리즘이다. 모든 샘플에 대해 손실을 계산하고 이를 기반으로 가중치를 업데이트한다. 하지만 모든 샘플을 사용하여 계산하면 연산량이 너무 많아진다. 이 문제를 해결하기 위해 Stochastic Gradient Descent(SGD)를 사용한다.

용어 정리
epoch: 전체 데이터셋을 한 번 모두 학습하는 횟수. 예를 들어, 1000개의 트레이닝 데이터를 10번 학습하면(epoch=10), 총 10000개의 데이터를 보게 된다.iteration: 모델의 파라미터를 업데이트하는 횟수. batch 사이즈 만큼의 데이터를 학습할 때마다 한 번 parameter를 update한다. 예를 들어, 1000개의 데이터를 배치 사이즈 100으로 학습하면, 1 epoch에 10번의 iteration이 발생한여 1번 학습(1 epoch) 하는데 10번 파라미터가 업데이트 된다.step: parameter 한 번의 업데이트를 의미.batch: 파라미터 업데이트에 사용되는 데이터의 수. iteration수 배치 사이즈가 1인 경우는 온라인 학습(online learning)이라고 한다.
Backpropagation
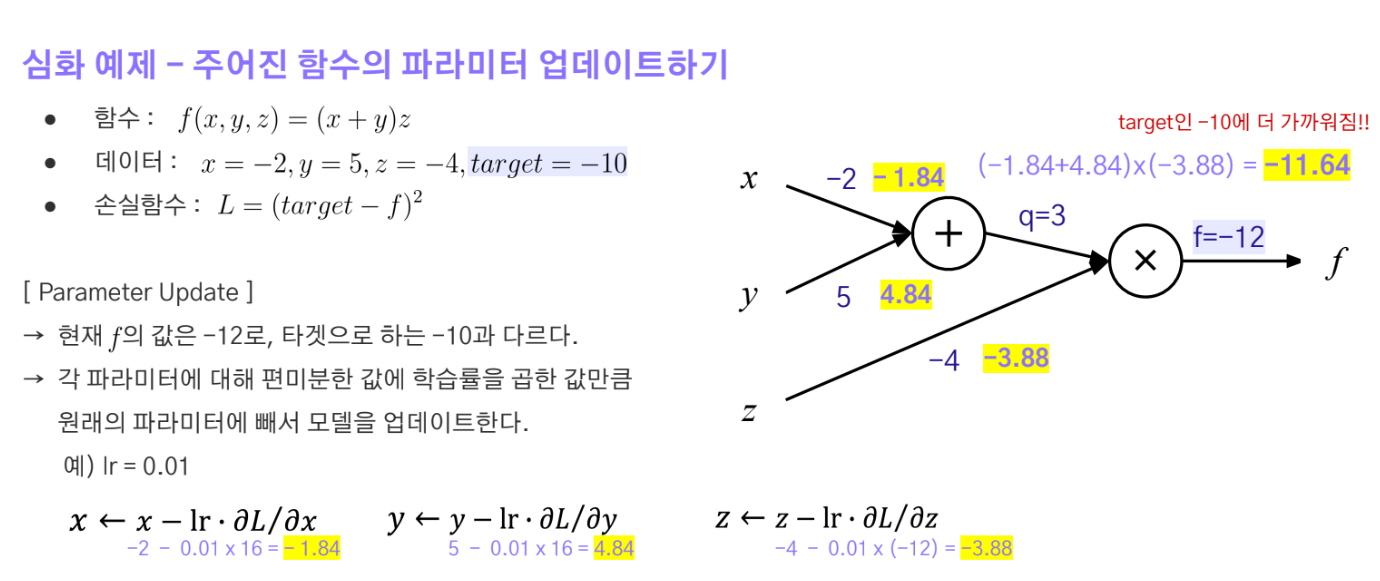
Backpropagation은 gradient descent를 딥러닝 모델에 적용하기 위한 방법이다. Layer가 굉장히 많은 딥러닝모델에서 각각의 가중치를 업데이트 하기 위해서는 Loss를 각각의 파라미터로 편미분 해야하는데 이를 연쇄법칙을 이용하여 다음 노드의 편미분계수를 사용해서 지금 노드의 편미분계수를 얻어 가중치를 업데이트 하는 방식이다.
Batch Normalization
Batch normalization은 모델이 안정적으로 학습할 수 있도록 도와준다. 배치 단위의 데이터셋 분포를 표준 정규 분포로 맞추는 기법이다.
Batch Normalization의 이유
- 활성화 함수(activation function)를 여러 층을 거쳐 통과하면 값이 점점 작아지거나 커지면서 학습이 어려워진다. 예를 들어, 처음에는 0~1 사이의 값이 0.5~0.7, 나중에는 0.6~0.7로 쏠리면서 편향이 생긴다.
- 이는 gradient vanishing(기울기 소실)이나 gradient exploding(기울기 폭발) 문제로 이어질 수 있다.
-
데이터 분포의 변화:
깊은 신경망에서 각 레이어를 통과할 때마다 데이터의 분포가 변화합니다. 활성화 함수(특히 비선형 함수)를 거치면서 이 변화가 더욱 심해집니다. -
그래디언트 소실(Vanishing Gradient):
깊은 네트워크에서 역전파 과정 중 그래디언트가 점점 작아져 앞쪽 레이어에 거의 도달하지 못하는 현상입니다. 이로 인해 네트워크의 앞부분이 효과적으로 학습되지 않습니다. -
그래디언트 폭발(Exploding Gradient):
반대로, 그래디언트가 너무 커져서 가중치 업데이트가 불안정해지는 현상입니다. 이는 학습을 불안정하게 만들고 발산시킬 수 있습니다.
Batch Normalization이 이러한 문제들을 해결하는 방식:
-
데이터 정규화:
각 레이어의 입력을 정규화하여 일정한 분포를 유지합니다. 이는 활성화 함수의 입력이 적절한 범위에 있도록 보장합니다. -
내부 공변량 변화 감소:
각 레이어의 입력 분포를 안정화시켜 이전 레이어의 파라미터 변화에 덜 민감하게 만듭니다. -
그래디언트 흐름 개선:
정규화된 입력으로 인해 그래디언트가 더 원활하게 흐르게 되어 그래디언트 소실/폭발 문제를 완화합니다. -
학습 속도 향상:
안정된 입력 분포로 인해 더 높은 학습률을 사용할 수 있어 학습 속도가 빨라집니다.
하지만 시계열 데이터에는 batch normalization이 적합하지 않다. 데이터 샘플별로 길이가 다르기 때문이다. 이런 경우, Layer normalization을 사용한다.
가중치 초기화
가중치 초기화는 학습 전에 한 번 수행되며, 초기 가중치의 설정은 학습의 효율성에 큰 영향을 미친다.
Xavier 초기화
Xavier 초기화는 주로 Sigmoid 활성화 함수와 함께 사용된다. 이는 가중치가 너무 크거나 작지 않도록 설정하여 학습 초기의 불안정을 줄인다.
He 초기화
He 초기화는 주로 ReLU 활성화 함수와 함께 사용된다. 이는 ReLU가 음수 영역을 모두 날려버리기 때문에 가중치를 적절히 초기화하여 출력 범위의 불안정을 줄인다.