챕터4. BASIC REFINEMENTS IN INTEREST RATE RISK MANAGEMENT

이 장에서는 채권 가격과 이자율 사이의 관계가 선형이 아니라는 것을 깨닫고 동시에 이자율 기간 구조가 평행 이동하지 않는다는 것을 깨닫는다. 이후 이러한 상황에서 위험 관리 전략을 어떻게 조정할 것인지 전략을 일반화하는 법을 배운다.

---

✏️Convexity

채권 가격과 이자율은 선형 관계가 아닌 볼록한 관계를 가진다
이자율이 올라갈수록 채권의 가격은 하락하지만 이러한 하락은 점점 둔화된다

직선이 아닌 볼록성을 가지기 때문에 아주 작은 변화에서만 차이가 적어 듀레이션이 통한다
큰 범위에서 더 적절한 값을 얻기 위해서는 이자율 변화에 따른 채권의 볼록성을 고려해야 한다
이러한 볼록성은 2계도함수로부터 유추해낼 수 있다

채권의 볼록성

$Convexity = C = {1\over P}{d^2 P\over dr^2}$

이러한 볼록성을 고려하여 가격의 증가율을 구하면 다음과 같다

${dP\over P} = -D\times dr + {1\over 2}\times C\times dr^2$

참고: 테일러 급수
https://ko.wikipedia.org/wiki/%ED%85%8C%EC%9D%BC%EB%9F%AC_%EA%B8%89%EC%88%98

무이표채의 볼록성

$C_z = (T-t)^2$

포트폴리오의 볼록성을 구하는 방법은 듀레이션을 구하는 방법과 동일하게 가중평균하면 된다

이표채의 볼록성

$C = {1\over P_c(t,T)}\times [\displaystyle\sum_{i=0}^{n-1}{c\over 2}\times P_z(t,T_i)\times (T_i - t)^2 + (1+{c\over 2})\times P_z(t,T_n)\times (T_n - t)^2]$

양의 볼록성: 평균 수익률에 대한 Good News

금리 변화를 장기적으로 예상하는 것은 가능할 수 있어도 단기적, 매일매일의 금리 변화를 예측하는 것은 매우 어렵다

금리 수준의 변화(dr)를 안다면 듀레이션을 곱하여 얼마만큼의 손실을 볼지 예상할 수 있다
하지만 단기적인 변화를 예상하기 어렵기 때문에 장기적인 예상을 해야할 것이고 이때 C가 필요하다

이를 고려하였을 때 예상 수익은 다음과 같다
$E[{dP\over P}]=-D\times E[dr] + {1\over 2}\times C\times E[dr^2]$

여기서 $E[dr^2]$은 무엇일까? 이는 이자율 수준 변화의 분산에 상응하며 이자율 변동의 크기를 의미한다
실수의 제곱은 0보다 크며 이에 대한 평균도 0보다 크다. 따라서 이자율이 내일 어떠한 방향으로 움직일지는 모르지만 어느 방향이든 움직일 가능성이 매우 높다는 것이다

이러한 움직인은 장기적으로 보았을 때 큰 위험에 대한 대가가 될 것이다

Common Pitfall

⭐볼록성은 듀레이션의 변화가 아니다
금리 변화에 상관 없이 만기가 동일하다면 무이표채에 대한 듀레이션은 일정하다
하지만 무이표채의 볼록성은 0이 아니다

볼록성은 단지 미분을 통해 얻은 기울기의 변화와 같다

금액 볼록성은 양으로 불리우며 다음과 같다

$Dollar convexity = C^{\$} = {d^2 P\over dr^2}$

볼록성과 위험 관리

볼록성을 고려하였을 때 이자율 위험 관리에 대한 수행능력은 향상한다

기업의 포트폴이오가 이표채와 k개의 무이표채로 구성되어 있다
이때 듀레이션 면역 전략을 사용하여 dV=0으로 만드려고 한다

$V=P+k\times P_z(0,T)$

$d\,V=-(D\times P + k\times D_z\times P_z)\times dr + {1\over 2}\times (P\times C + k\times P_z\times C)\times dr^2$

첫번째 괄호는 듀레이션 헤징으로만 0을 만들 수 있지만 뒤의 괄호는 그럴 수 없다
만약 이 부분이 음수라면 $dr^2 > 0$이기에 금리가 오르든 내리든 변화하기만 하면 손해를 보게 된다
반대로 이 부분이 양수라면 금리가 변화하기마 하면 이익을 얻을 수 있다

따라서 듀레이션 헤지는 뒤의 괄호까지 0으로 만들기 위한 k와 T를 찾아야 한다

듀레이션과 볼록성을 헤지할 상품이 늘어나면 선택의 폭이 늘어나기 때문에 더 쉽게 전략을 시행할 수 있다

볼록성 거래와 시간의 흐름

볼록성이 높은 장기채를 구매하고 볼록성이 낮은 단기채 상품을 이용하여 금리 위험을 헤지하면 볼록성으로 이익을 얻을 수 있다
즉, 앞의 식에서 첫번째 괄호 안의 식을 0으로, 뒤의 괄호 부분을 양수로 만든 것이다

바벨포트폴리오: 듀레이션이 큰 채권과 낮은 채권을 구입한다
불릿포트폴리오: 중간정도의 듀레이션을 지닌 채권을 구입한다

볼록성 거래 전략: long barbel and short bullet position with the same duration

이러한 전략으로 차익거래 기회가 존재하지 않는 이유

세타-감마 관계로 알려진 시간경과에 따라 높은 볼록성으로 얻은 이익을 상쇄시킨다는 점이 간과되어 있기 때문이다. 사실 무이표채처럼 시간이 경과함에 따라 이자율이 변하지 않아도 시간의 가치를 얻을 수 있다. 하지만 이러한 사실이 볼록성 거래 전략과 듀레이션 헤지에는 고려되지 않았기 때문에 여기서 발생한 이익은 시간에 따른 가치에 상쇄될 것이다

✏️Slope and Curvature

고정 금리 상품에 투자하거나 위험 관리를 할 때 일반적인 금리 수준(평균)과 그 기울기를 확인하여야 한다
하지만 이자율 기간 구조가 위 아래로 평행하게 이동하지는 않는다
만약 평행하게 움직였다면 각각의 이자율은 같은 거리를 유지하고 있겠지만 사실은 그렇지 않다

보통 10년물과 1월물의 차이인 기간 스프레드는 시간에 따라 크게 변동하며 -5%에서 5% 사이로 움직인다
이러한 움직임은 금리 수준을 변화시킬수도 있고 그렇지 않을 수도 있다

금리수준 다음으로 확인해야할 것은 이자율 기간 구조의 곡률이다
이는 기간 구조의 수준(평균)과 기울기로 설명할 수 없이 다양하며 단기, 중기, 장기 채권의 상대적 가격을 결정한다

기간 구조의 곡률을 측정하는 방법 중 하나는 단기, 중기, 장기 채권의 상대적 가격을 고려하는 것이다
대중적인 방법으로는 나비 스프레드로 불리는 것이 있으며 다음과 같다

나비스프레드

$Curvature = -Short\;term\; yield + 2\times Medium\;term\; yield - Long\;term\; yield$

리스크 관리에 미치는 영향

기울기와 곡률이 위험 관리에 중요한 이유
: 앞에서 언급하였듯이 기본적으로 금리 수준의 평균적인 변화에 대해서는 기울기로 헤지가 가능하지만
이자율 기간 구조가 평행하게 움직이지 않기 때문에 오차를 줄이기 위하여 곡률이 사용된다

즉, 듀레이션 헤지가 가능한 포트폴리오라고 하더라도 아직 기울기와 볼록성으로부터 큰 손실을 야기할 수 있다

면역전략을 사용할 때 듀레이션만 맞추고 나두면 안 된다
곡률이 존재하기 때문에 시간이 지나면서 기울기가 변화하기 때문에 손해를 볼 수 있다

팩터 모델과 팩터 중립

이자율 기간 구조를 도출하는 팩터로서 금리 수준(평균), 기울기, 곡률을 고려

팩터 모형

$dr_1 = \beta_{11}d\phi_1+\beta_{12}d\phi2 + \cdots + \beta_{1m}d\phi_m$
$dr_2 = \beta_{21}d\phi_1+\beta_{22}d\phi2 + \cdots + \beta_{2m}d\phi_m$
$\;\;\vdots \qquad\qquad\qquad\qquad \vdots$
$dr_n = \beta_{n1}d\phi_1+\beta_{n2}d\phi2 + \cdots + \beta_{nm}d\phi_m$

$\beta_{ij}$는 각 팩터(j)의 변화가 개별 이자율(i)에 미치는 영향을 결정한다

듀레이션 기반 위험 관리의 경우 평행 이동만을 고려하였다.
즉, 병렬 이동이라고 불리는 요인(위의 j = 1)과 $\beta_{i1} = 1$인 것 모두를 고려하였다.
이 경우 "팩터 $\phi_1$"의 증가는 모든 지점 T1,...,Tn에서 이자율 기간 구조의 전반적인 증가를 발생시켰다.
위에서 팩터2는 기울기이며 팩터3은 곡률이라는 것을 일반화하였다

이때 베타가 주어진다면 팩터가 변화함에 따라 미치는 영향을 중립화할 수 있다

팩터 듀레이션

팩터 j에 따른 가격이 P인 자산의 팩터 듀레이션

$D_j = -{1\over P}{d\, P\over d\, \phi_j}$

이때 ${d\, P\over d\, \phi_j}$은 팩터 j의 변화에 따른 가격 민감도를 나타낸다

팩터j의 변화($d\phi_j$)는 무이표채의 만기에 상응하는 수익률에 영향을 미친다
이러한 영향력의 크기는 상관계수 $\beta_{ij}$에 의해 결정된다

팩터 j만 움직일 경우, $dr_i = \beta_{ij} d\phi_j$

또한 $dr_i$의 변화는 무이표채에 영향을 주기 때문에 도미노 효과가 발생한다

${dP_z(t,T_i)\over d\phi_j} = {dP_z(t,T_i)\over dr_i}\times \beta{ij}$

$D_{j,z} = (T_i -t)\times \beta_{ij}$

이 형식은 듀레이션과 비슷하다
만약 금리 수준 팩터에 대하여 $\beta_{i1} \approx 1$이라면 일반적인 듀레이션 식을 얻을 수 있다

더 나아가 기울기와 곡률도 고려하여 채권 가격의 변화율을 계산하는 방법은 다음과 같다

${dP\over P} = -D_1\times d\phi_1 - D_2\times d\phi_2 - D_3\times d\phi_3$

팩터 중립

포트폴리오 P에 대한 듀레이션 팩터가 각각 금리 수준과 기울기라 하자
팩터 중립을 위해 두 가지 상품을 선택해야 한다
이 때 단기채와 장기채를 조합하기로 하였다면 금리 수준과 기울기 면역을 위해 개수를 정해야 한다

$V = P + K_S\times P^S_z + k_L\times P^L_z$

$dV = dP + K_F\times dP^S_z + k_L\times dP^L_z=0$

$K_S\times D^S_{z1}\times P^S_z + K_L\times D^L_{z1}\times P^L_z = -D_1\times P$
$K_S\times D^S_{z2}\times P^S_z + K_L\times D^L_{z2}\times P^L_z = -D_2\times P$

팩터 모형의 추정($\beta_{ij}$는 어디서 오는 걸까?)

수익률과 팩터에 대한 과거 데이터로 베타를 추정할 수 있다

각각의 만기가 주어지고 이를 고정하였다고 하자. 그리고 과거 데이터의 시간 간격을 h라 하자

이때 만기 $\tau_i에 대한 무이표채 수익률의 변화는 다음과 같다

$\Delta r_i(t) =r(t+h, t+h+\tau_i)-r(t,t+\tau_i)$

$\Delta r_1(t) = \alpha_1+\beta_{11}\Delta\phi_1(t)+\beta_{12}\Delta\phi_2(t)+\beta_{13}\Delta\phi_3(t)+\epsilon_1(t)$
$\Delta r_2(t) = \alpha_2+\beta_{21}\Delta\phi_1(t)+\beta_{22}\Delta\phi_2(t)+\beta_{23}\Delta\phi_3(t)+\epsilon_2(t)$
$\quad\vdots$
$\Delta r_n(t) = \alpha_n+\beta_{n1}\Delta\phi_1(t)+\beta_{n2}\Delta\phi_2(t)+\beta_{n3}\Delta\phi_3(t)+\epsilon_n(t)$

여기서 입실론은 팩터 모형이 완벽하지 않을 가능성을 내포하며
알파는 팩터로 가정되지 않은 이자율 변동의 평균이다

수익률 $r_i(t)$과 팩터 $\phi_j(t)$ 데이터가 주어진다면 선형회귀분석을 바탕으로
상관계수인 $\beta_{if}$를 도출해낼 수 있다

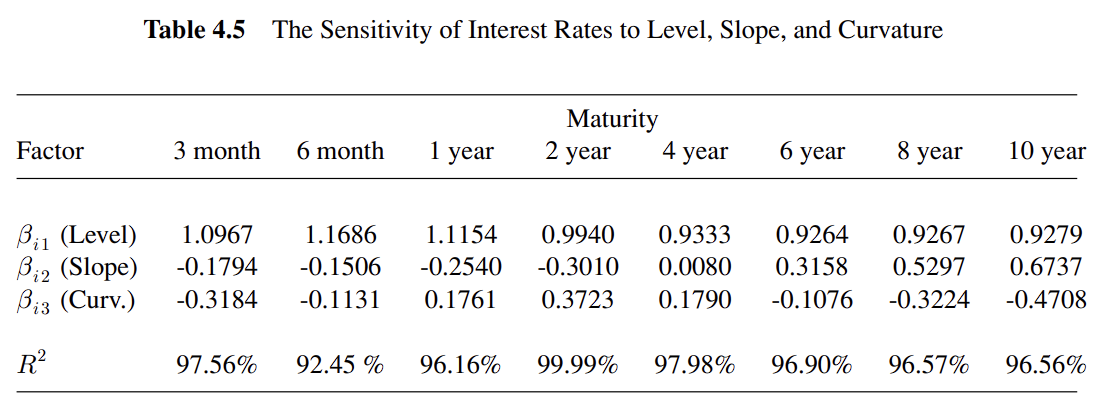
• 수준 팩터에 대한 $\beta$: 모든 수익률은 나란히 오르내리기 때문에 1에 가깝다
• 기울기 팩터에 대한 $\beta$: 짧은 만기에 대해 음수이고 긴 만기에 대해 양수이다
  기울기가 증가하면 단기 수익률을 낮추고 장기 수익률을 올린다는 의미이다
• 곡률 팩터에 대한 $\beta$: 단기 및 장기채에 대하여 음수이고 중기채에 대해 양수이다
  팩터가 증가하면 단기 및 장기 수익률은 감소하지만 중기 수익률은 증가한다는 의미이다

회귀분석 결과 보고서에서의 $R^2$
$R^2$는 회귀분석에서 결정계수라 불리우며 독립변수가 종속변수를 얼마나 잘 설명하고 있는지 보여준다

따라서 여기서는 시간에 따른 기간구조의 움직임을 설명해주는 세가지 변수가 얼만큼의 파워를 가지는지 보여준다

예를 들어, 4년 만기 금리에 대해 $R^2=99.99\%$라면
4년물의 수익률 변화는 수준, 기울기, 곡률에 의해 완전히 설명된다는 의미이다

이러한 사실이 중요한 이유는 높은 설명력을 가진 변수들로만 리스크 관리를 하여
더 효율적인 헤지가 가능하기 때문이다