챕터5. INTEREST RATE DERIVATIVES: FORWARDS AND SWAPS

전통적으로 파생상품은 기초 자산에 의해 가치가 결정되었지만
이자율 파생상품에 대한 시장의 크기가 주요 시장보다 커지면서
기초 자산이 먼저인지 파생상품 시장이 먼저인지 확실히 할 수 없게 되었다

따라서 차익거래가 발생하지 않는 관계를 바탕으로 가치를 계산하는 법을 배운다

---

✏️선도 이자율과 선도 할인 요소

선도 이자율을 구하기 위한 트레이딩 전략 예시

Today	$T_1$	$T_2$
Sell short $97.728m of T-bills	Receive $100m from firm, close short
Buy $M=1.02105={97.728\over 95.713}$		Receive 1.02105*100m, give total to firm
Total Net Cash Flow = 0	Total Net Cash Flow = 0	Total Net Cash Flow = 0

$100m의 기계장치를 판매하였고 6개월 후 ($T_1=0.5$) 에 돈을 받는다고 하자
하지만 이 회사는 6개월 뒤에는 돈을 사용할 곳이 없고 그로부터 6개월 뒤( $T_2=1$ )에 돈이 필요하다
그렇기에 $T_1$부터 $T_2$사이에 이자율을 고려하여야 할 것이고 시장에서 이를 선도금리라 하며
$f_2 = 4.21\%$로 나타낸다 그렇다면 이$f_2$는 어떻게 계산되었을까?

By no arbitrage

현재 시점에서 $Z(0.5,1)$은 알지 못하기 때문에 이를 선도 할인율이라 부른다

$F(t,T_1,T_2) = {Z(t,T_2)\over Z(t,T_1)}

이는 다음과 같은 특징이 있다

$1.\;\; F(t,T_1,T_2) = 1 for T_2=T_1$
$2.\;\; F(t,T_1,T_2) is\; decreasing\; in\; T_2$

이제 미래 시점의 할인율을 알았기 때문에 선도 이자율을 구할 수 있다

(semi-annual compounding)
$f_n(t,T_1,T_2)=n\times ({1\over {F(t,T_1,T_2)^{1\over n\times (T_2 - T_1)}}}-1)$

만약 continuosly compounded를 가정한다면

$f_n(t,T_1,T_2)=-{ln(F(t,T_1,T_2))\over {T_2-T_1}}$

할인율을 이용하여 선도이자율을 구한 것 처럼 역으로 선도이자율을 이용하여 할인율을 구할 수 있다

차익거래가 없을 시 선도 이자율

아래의 두 전략을 살펴보자

• Strategy 1. 만기가 $T_2$인 무이표채 $W만큼 구매
• Strategy 2. 만기가 $T_1$인 무이표채를 구매하고 선도 이자율을 활용

이 두 전략은 $T_2$시점에 다른 위험 없이 같은 양의 돈을 얻기에 payoff가 서로 같아야 한다

$Strategy\, 1 = ({\$W\over P_z(t,T_2)})\times \$100$

$Strategy\, 2 = [({\$W\over P_z(t,T_1)})\times \$100]\times (1+f_2/2)^{2\times (T_2-T_1)}$

$(1+f_2/2)^{2\times (T_2-T_1)}={Z(t,T_1)\over Z(t,T_2)}$
이를 $f_2$에 대하여 전개하면 위의 $f_n$의 식에서 n에 2를 넣은 것과 같다

The Forward Curve

(아래의 글은 continuously compounding을 가정한다)

미래의 특정시점에 예상되는 선도금리들을 연결해놓은 선, 선도금리와 투자 시점 T에 대한 관계
이는 미래 명목 이자율에 대한 시장의 기대와 투자자들의 위험 회피 정도에 따라 달라진다

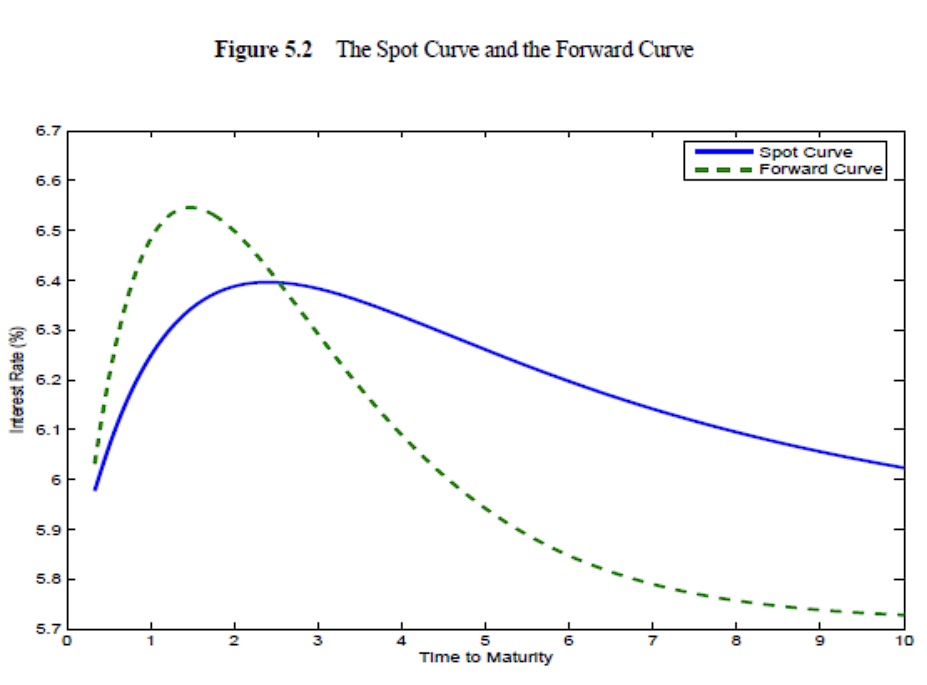
포워드 커브와 스팟 커브는 같이 움직이는 것처럼 보인다
알다시피 포워드 커브가 스팟 커브를 결정하는 할인율과 동일한 할인율을 이용하기 때문이다

나아가 선도이자율과 현물이자율의 관계를 알아보자

$f(0,T,T+\Delta)=r(0,T)+(T+\Delta)\times {r(0,T+\Delta)-r(0,T)\over \Delta}$

스팟 커브가 상승하면($\Delta$가 positive) 포워드 커브는 스팟 커브 위에 있고
스팟 커브가 하락하면($\Delta$가 negative) 포워드 커브는 스팟 커브 아래 있다
(스팟 커브가 flat하면 서로 같다)

이 관계를 더 이해하기 쉽게 $T_{i+1}=T_i+\Delta$이고 $T_1=\Delta$라고 가정해보자

따라서 $\qquad\; Z(0,T_{i+1})=Z(0,T_i)\times F(t,T_i,T_{i+1})$ 이며,
이에 따라 $r(0,T_n)\times T_n = (r(0,T_1)\times \Delta + f(0,T_1,T_2)\times \Delta + \dots +f(0,T_{n-1},T_n)\times \Delta)$ 이다.

즉, continuously compounded spot rate는 $T_n$까지의 선도 이자율의 평균과 같다
$이때\;\; T_0=0\; 이고\; f(0,0,T_1) = r(0,T_1)\;으로 한다$

T가 만기인 현물이자율이 선도 이자율의 평균과 같기 때문에
선도 이자율이 현물 이자율보다 위에 있다면 현물 이자율이 증가한다는 것을 더 쉽게 이해할 수 있다

선도 이자율로 부터 이자율 커브 추출

때때로 할인율 $Z(0,T)$를 계산하기 위한 무이표채가 이용가능하지 않을 수 있다
이때 선도 이자율을 사용하여 선도 할인율을 계산하고 이를 통해 수익률 곡선을 추출할 수 있다

$Z(0,T_i)=Z(0,T_{i-1})\times e^{-f(0,T_{i-1},T_i)\times 0.25}$

Spot rate $r(0,T_i)=-{ln(Z(0,T_i))\over T_i}$

✏️FRA

Forward Rate Agreement는 두 거래상대방간의 계약으로, 한 거래상대방은 T1에서 T2까지의 기간 동안 명목 원금 N에 대해 선도 금리 $f_n (0, T_1, T_2)$을 지불하기로 합의하고,
다른 거래상대방은 미래의 시장 변동 금리 $r_n (T_1, T_2)$에 따라 지불하기로 합의한다

$Net\; payment=N\times \Delta\times [r_n(T_1,T_2)-f_n(0,T_1,T_2)]$

이때 $\Delta=T_2-T_1$이며 $n=1/\Delta$이다

FRA의 가치

거래 개시 시점에서는 교환 비용이 발생하지 않아 가치가 0이다
하지만 시간이 지나며 선도 이자율이 변함에 따라 FRA의 가치는 변화한다

$V_{FRA}(t)=M\times P_{bill}(t,T_2)-P_{bill}(t,T_1)$

recall $M=P_{bill}(t,T_1)/P_{bill}(t,T_2)$
따라서 $t=0$일때 $V_{FRA}=0$

이번에는 상대방에게 계약 종료를 물어보는 형태가 아닌 제3자와 새로운 FRA계약을 체결하여
같은 효과를 누리는 상황을 생각해보자

$Payoff\; of\; reverse\; FRA\; at\; T_2={N\over 2}\times [r_2(T_1,T_2)-f_2(t,T_1,T_2)]$
여기서 주의할 점은 현재의 선도 이자율에 영향을 받는다는 점이다

이렇게 새로운 계약의 payoff와 이전 계약의 payoff가 다르기 때문에
이 차이의 현재가치 만큼이 FRA의 가치가 될 것이다

$V_{FRA}=Z(t,T_2)\times {N\over 2}\times [f_2(0,T_1,T_2)=f_2(t,T_1,T_2)]$

✏️선도 계약

FRA는 미래의 현물 이자율과 선도 이자율을 거래하는 것이었다
이와 비슷한 방식으로 미래의 수익률을 고정하는 방법이 있다
현재 시점에서 미래 채권 가격을 합의하여 결정하는 것이다

이러한 계약을 선도계약이라고 하며 이때 합의된 가격을 선도가격이라고 한다

$P^{fwd}(0,T,T^{*})$은 만기가 $T^{*}$이며 $T$시점에 인도되는 현재시점의 선도 가격이다

이때 $T$시점에 상품의 가치가 $P(T,T^{*})$이라고 한다면 선도계약의 payoff는 다음과 같다

$Payoff = P(T,T^{*})-P^{fwd}(0,T,T^{*})$

이러한 payoff를 이용하여 수익률을 연율화하면 다음과 같다

$Annualized\; rate\; of\; return = {1\over T_2-T_1}\times ({Payoff\; at\; T_2\over Investment\; at\; T_1}-1)$

No Arbitrage Argument

무이표채의 선도가격이 선도 할인율 $\times$ 100 보다 크다고 가정해보자
이때 차익거래자들은 다음과 같은 전략을 세울 수 있다

• 선도 가격에 무이표채 선도 판매한다
• 선도 할인율과 만기가 T인 무이표채를 이용하여 만기가 $T^{*}$인 무이표채를 구매한다

선도 계약의 가치

T시점에 인도된 T-bond의 만기가 $T^{*}$이며 이 사이의 기간동안 c만큼 항상 쿠폰을 주는 상황이다

이때 계약의 가치 $V^{fwd}(t)=Z(t,T)\times [P_c^{fwd}(t,T,T^{*})-K]$ 이다

$K = P_c^{fwd}(0,T,T^{*})$ 개시시점에 합의된 행사가격

---

선도가격과 선도계약의 가치를 혼동하는 경우가 많다
선도가격은 한 트레이더가 선도계약을 매수할 수 있는 가격이 아니다
실제로 개시시점 $t=0$ 에서 거래상대방 사이에 교환이 이루어지지 않기 때문에
선도계약을 체결하는 데는 아무런 비용이 들지 않는다
그 이유는 선도계약은 미래에 (오늘날이 아닌) 환전을 하기 위한 오늘의 합의이기 때문이다
선도가격은 미래에 증권을 매수하거나 매도하기로 오늘날 우리가 합의하는 가격이다

그러나 일단 계약이 개시되고 선도가격이 설정되면, 오래된 선도계약의 가치는 시간의 흐름에 따라
이자율의 변동이나 기초 증권의 변동에 따라 변하게 된다.
따라서 이 오래된 선도가격으로 계약을 진행하기 위해서는 그만큼의 대가를 지불해야만 하며
이를 선도계약의 가치라고 한다

---

✏️금리스왑

A plain vanilla swap(표준형 금리스왑)은 만기까지 고정금리 쿠폰과 변동금리 쿠폰을 교환하는 계약이다

$Net\; payment\; at\; T_i=N\times \Delta\times [r_n(T_{i-1})-c]$

The constant c is called swap rate

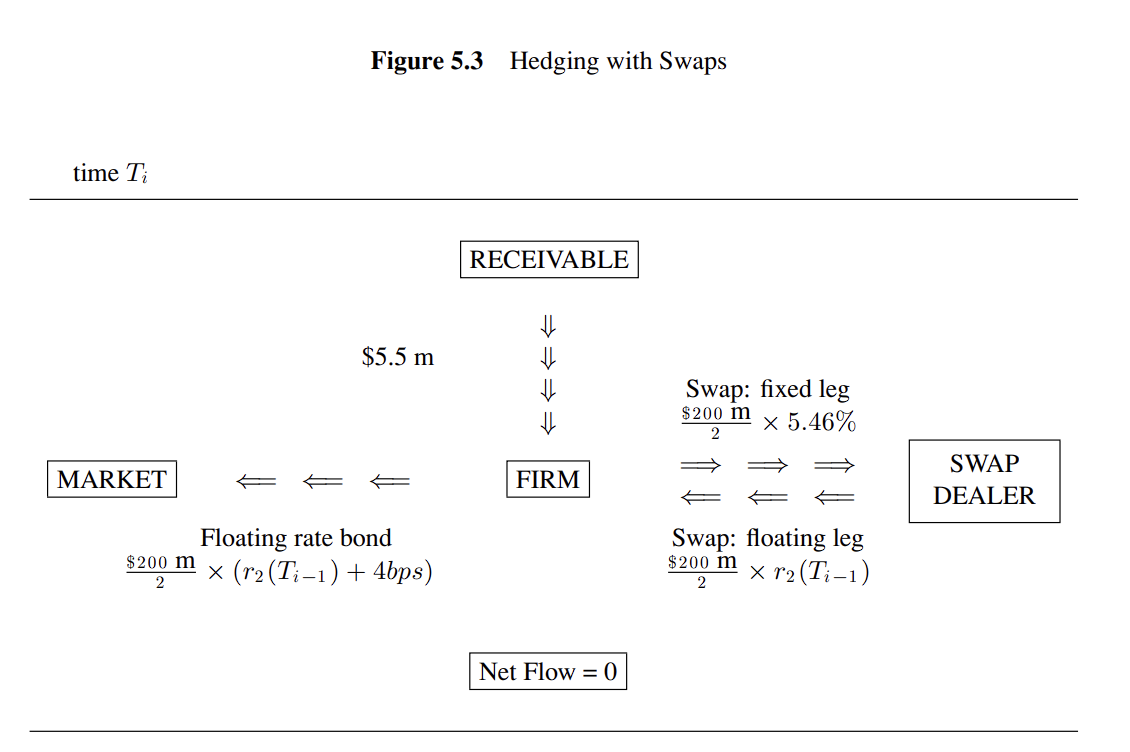
회사가 변동금리를 이용했을 경우 리보금리가 0.51%이상 오를 경우 손해를 보게 된다
따라서 이 회사는 은행과 스왑계약을 함으로써 리보금리만큼 받고 5.46%만큼 고정으로 지급한다
결과적으로 회사는 5.46%+4bp인 5.5%만큼 비용이 발생하기 때문에 총 현금흐름은 0이 되며 완벽한 헤지가 된다

이처럼 스왑계약을 통해 고정현금흐름을 발생하게 하여 변동현금흐름을 헤지할 수 있다

스왑의 가치

고정금리를 이용하고 있는 거래자를 생각해보자
이 사람은 변동금리채권에 long, 고정금리채권에 short 포지션을 취하며 스왑과 같은 효과를 누릴 수 있다

즉, $V^{swap}(t;c,T)=P_{FR}(t,T)-P_c(t,T)이다

이자 지급 날짜를 $T_i$라 하면 이때 변동금리채권의 가치는 100일 것이며 이때 스왑의 가치는 다음과 같다

$V^{swap}(T_i;c,T)=100-({c\over 2}\times 100\times \displaystyle\sum_{j=i+1}^{M}{Z(T_i,T_j)}+Z(T_i,T_M)\times 100)$

스왑비율

그렇다면 이제 스왑비율 c가 어떻게 결정되는지 알아보자
스왑계약을 맺는 시점에서 가치는 0이라는 것을 이용하여 이를 만족하는 c를 구할 수 있다

$c = n\times ({1-Z(0,T_M)\over \sum_{j=1}^{M}{Z(0,T_j)}})$

스왑커브

t시점의 스왑커브란 모든 만기에 대한 스왑 비율의 집합을 의미한다

스왑시장의 크기를 고려할 때 스왑 커브는 화폐의 시간 가치를 결정하는 참고 요인이 된다
따라서 스왑 커브를 이용하여 할인율을 계산할 수 있다

$i=1$일때

$Z(t,T_i) = {1\over 1+ {c(t,T_i)\over n}}$

$i$가 2이상일 때

$Z(t,T_i) = {1-{c(t,T_i)\over n}\times \sum_{j=1}^{i-1}{Z(t,T_j)}\over 1+{c(t,T_i)\over n}}$

리보 수익률 곡선과 스왑 스프레드

할인율을 구하는 방법 두가지를 알아보았다
첫째는 스왑금리를 활용하는 방안, 둘째는 T-bonds를 이용하는 방안이었다
그렇다면 이 둘은 어떠한 관계가 있을까?

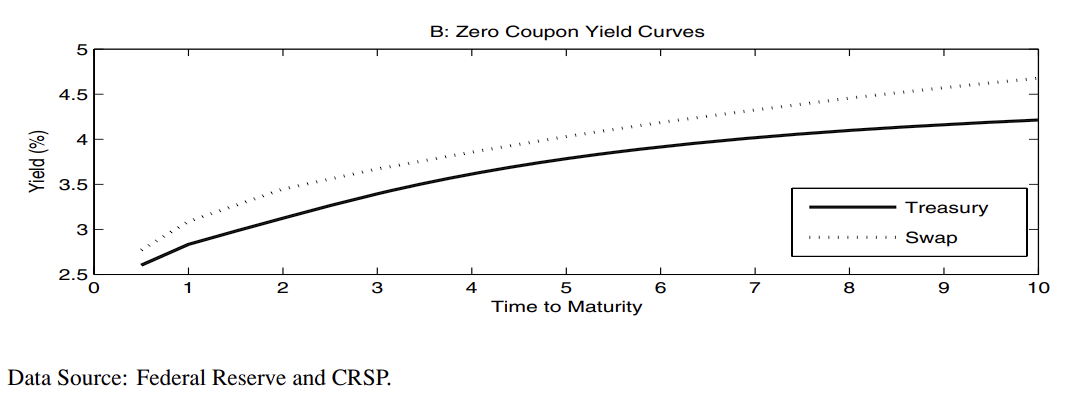
위의 그림을 보면 리보 수익률 곡선이 트레져리 수익률 곡선보다 높이 있다는 것을 확인할 수 있다
이러한 차이가 발생한 이유는 LIBOR 곡선에도 스왑 딜러의 부도 확률로 인한 스프레드가 포함되어 있기 때문이다.
이러한 스프레드는 일반적으로 매우 작지만 07-08년의 신용 위기와 같은 격동의 시기에 유의미하게 변할 수 있다.

스왑 스프레드가 클 때 투기자들은 미래에 스프레드가 줄어들 것에 베팅한다
이때 T-bond는 short 포지션을 취하고 fixed for floating 스왑을 체결하여 전략을 구사한다

스왑 선도 계약, 선도 스왑률

위의 금리 선도와 비슷한 내용이다

forward swap: 미래에 두 거래상대방이 forward swap rate라는 미리 정해진 비율로 스왑 계약을 체결
이때 T시점에 시행하여 $T^{*}$시점에 종료되는 계약의 forward swap rate는 다음과 같다

$f_n^s(0,T,T^{*})=n\times {1-F(0,T,T^{*})\over \sum_{j=1}^{m}{F(0,T,T_j)}}$

이 선도 스왑률을 유도하는 과정은 다음과 같다
먼저 우리는 스왑이 이표채에 롱 포지션, 변동금리채에 숏포지션과 같다는 것을 떠올리자

그렇다면 스왑의 $Payoff = P_c(T,T^{*})-100$이 될 것이다

이때 선도 계약 특징에 따라 이러한 payoff는 미래에 발생할 것이다

따라서 이를 현재가치화하면 $V(0,T) = Z(0,T)[P_c^{fwd}(0,T,T^{*})-100]$이 된다

그리고 표준화된 선도계약은 개시시점에 비용이 0이기 때문에 가치도 0일 것이다
그렇다면 $V(0,T) =0$을 만족하는 c가 $f_n^s(0,T,T^{*})$가 되는 것이다

지급 일수와 일수 계산 규칙

앞의 설명들은 두 거래 상대방의 지불기간이 동일할 때를 가정하였다
하지만 많은 스왑 거래들이 서로 다른 지불기간을 가지며 지급 빈도 또한 다르다

그렇다고해도 floating leg와 fixed leg를 독립적으로 계산할 수 있기에
이러한 차이가 가치평가 영향을 미치진 않는다

또 다른 문제인 Day count가 있다 앞에서는 actual/actual convention을 사용하였다
이를 조정하기 위해서 변동금리에 대해서는 actual/360을 고정금리에 30/360을 적용한다
이후 이에 따라 payoff또한 어느 정도 조정이 필요하다

주의해야할 점은 Day count로 인해 막대한 손실을 입을 가능성은 적지만
차익거래규칙과 고정금리상품의 근본적인 변화에 대하여 이해하지 못했을 경우의 손실은 크기에
Day count를 생략하더라도 이에 집중하여야 한다

파생상품을 이용한 이자율 위험 관리

표준형 금리 스왑은 진입시 비용이 들지 않지만 포트폴리오의 듀레이션을 변화시킬 수 있다

스왑의 금액 듀레이션

$D^{\$}_{swap}=D^{\$}_{floating}-D^{\$}_{fixed}$

따라서 이를 이용하여 적절한 양을 선택한다면 기간 구조의 평행이동에 따른
포트폴리오의 손실을 예방할 수 있습니다

$D^{\$}_{E}=D^{\$}_{A}+N\times D^{\$}_{swap}-D^{\$}_{L}$