챕터8. BASICS OF RESIDENTIAL MORTGAGE BACKED SECURITIES

---

MBS 시장은 위험을 더 감당할 수 있는 사람들에게 그 위험을 전달하는 중요한 역할을 한다

개인에 대한 모기지가 다른 사람에게 판매되는 이러한 과정을 증권화라고 하며
이 챕터에서 다양한 유형의 증권화를 다뤄보려 한다

✏️Securitization

몇몇 기관이 자신들에게 위험한 자산을 들고 있다고 생각해보자.
그리고 그들은 리스크를 더 잘 감당할 수 있는 투자자에게 이를 팔려고 한다

이때 이 자산을 충분히 diversified하기 어려워 합리적인 가격에 팔 수 없다고 해보자

기관들은 비슷한 자산을 모아 각 자산에 포함된 위험을 분산시키는 포트폴리오를 만들어 투자자에게 팔면된다

이때 자산들을 모으기 위해 각 기관은 SPV라는 회사를 만들어 투자자들로부터 자금을 모을 수 있다

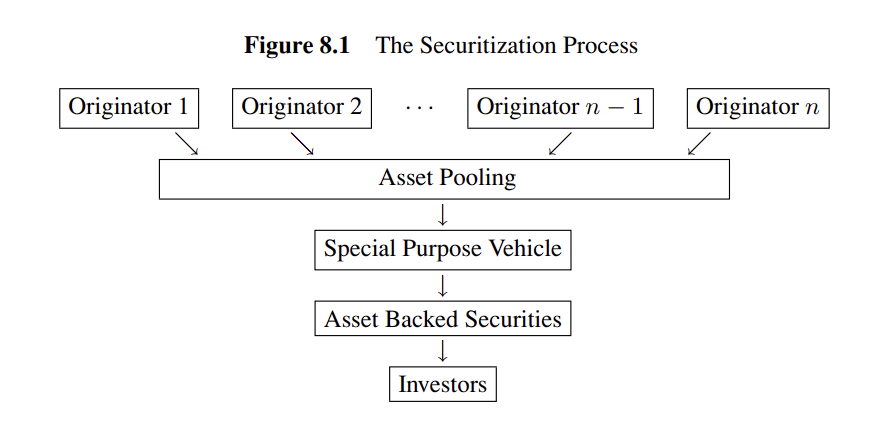
originatior: 자산을 모아 팔고자 하는 기관
issuer: 기관들로부터 자산을 구매하는 SPV

RMBS 시장의 주요 참여자

• Ginnie Mae: 정부 프로그램을 통해 만들어진 대출 상품을 담보로 하는 MBS에 대하여 적시 지급을 보증한다

• Fannie Mae: 금융 위기전까지는 주식회사였으나 지금은 정부의 관리를 받고 있다. Fannie Mae를 통해 증권화된 모기지에 대해 용보증을 제공하고 대규모 주택담보대출 포트폴리오를 보수하고
  부채를 발행해 포트폴리오를 파이낸싱한다

• Freddie Mac: 미 주택 담보 시장을 안정시키고 주택 소유와 저렴한 임대 주택의 기회를 확대하기 위해
  정부에 의해 charter되었으며 비즈니스 모델은 Fannie Mae와 같다

Private Labels과 세계 금융 위기

정부기관뿐 아니라 다른 기관들도 MBS를 발행하였다

정부 기관의 발행 비율이 크지만 다른 기관들의 발행량도 미국의 집값이 증가함에 따라 2007년까지 꾸준히 증가하였다

또한 이러한 증가는 agency morgage가 규제를 받았다는 이유도 있다
이들은 정해진 컷오프 이하의 양만 투자할 수 있었고 LTV도 최대 80%까지 가능하였다

이러한 규제는 부동산 시장이 과열됨에 따라 non-agency MBS가 위험을 감수하고 수요의 갭을 채워주도록 하였다

2007년, 2008년 금융위기와 부동산 가격의 하락은 투자자로 하여금 non-agency MBS의 구매를 경계하도록 하였다

이러한 수요의 감소는 높은 빚을 진 투자자에게 심각한 영향을 미쳤으며 이후 Fed에서는 몇 가지 정책을 내었다

Agency RMBS의 Default Risk와 Prepayment

신용 위기에 의해 채무 불이행이 발생하였고 채무 불이행으로 인해 많은 가구들이 파산하고 은행은 이 자산들을 헐값에 팔아야 했다

이때 default risk와 prepayment risk를 구분하여 볼 필요가 있다

✏️모기지와 중도상환 옵션

1년에 모기지 금리가 r%인 30년 fixed-rate mortgage가 있다고 해보자
이때 L이 은행에서 주택 소유자에게 빌려준 모기지의 양이라고 한다면 구하는 공식은 다음과 같다

$L=\displaystyle\sum_{i=1}^{30\times 12}{C\over (1+{r\over 12})^{i}}$

${1\over A} = 1+{r\over 12}$

$C={L\over \sum_{i=1}^{30\times 12}{A^i}}$

원리금 균등 상환

일반 채권의 경우 쿠폰은 원금에 대한 이자로만 구성되어 있으며 원금도 오직 만기에만 상환된다

반면에 모기지 채권의 경우 모기지 기간 동안 원금이 이자와 함께 상환된다
그렇기 때문에 원금이 많이 남을수록 쿠폰내 이자지급 비율이 크다

이러한 매커니즘을 고려하였을 때 t시점에 남은 원금은 식(8.8)과 같이 계산될 수 있다

$L_t = C\times A\times {1-A^n\over 1-A}$

이때 n은 모기지를 지불한 횟수

모기지 채권의 가격을 구하기 위하여 이 채권은 만기에 원금을 상환하지 않는 쿠폰만 존재하는 채권이라 생각하면 쉽다

$Value\; of\; mortgage\; debt=P(t)=\displaystyle\sum_{i=1}^{n}{C\over (1+r(t,T_i)/12)^i}$

여기서 $r$과 $r(t,T_i)$는 구별하여야 한다
$r$은 모기지 rate이며 $r(t,T_i)$는 할인을 위한 현물 금리이다

이때 주택 소유자의 입장을 고려해보자
이자율이 낮아질 경우 채권의 가격이 올라갈 것이고 이를 상환하여 새로운 계약을 체결함으로써
낮은 C payment를 지급하도록 할 수 있다

중도상환 옵션에 대한 위험

은행은 모기지 계약이 생성되고 나서 이에 대한 이자를 오래동안 받고 싶어한다
하지만 주택 소유자의 심리에 따라 언제든지 중도 상환할 수 있다
이 경우 이전의 이자율로 다시 계약을 진행할 수 없기 때문에 이러한 상황을 고려하여
은행은 처음부터 모기지 금리를 좀 더 높여서 받을 것이다

확실히 디폴트 리스크와 중도 상환 리스크는 돈을 받냐 못받냐라는 측면에서 다르다
하지만 흥미롭게도 주택 소유자의 디폴트는 대리인이 이를 중도상환하게 만들기 때문에
중도상환의 타이밍에 영향을 미친다

담보대출 중도 상환

전반적인 금리 수준이 중도 상환에 중요한 요인이지만 이뿐만 아니라 다양한 요인이 존재한다

• 계절성: 세금과 같은 이유로 여름에 이사가 많아 이때 조기상환이 이루어 진다

• 모기지 풀의 나이: 새로 가입된 모기지의 경우 높은 이자율과 낮은 원금으로 이루어져 있어
  이를 빠르게 갚아 비용을 아끼고자 한다
  하지만 refinancing에도 비용이 발생하기에 처음 몇년동안은 조기상환율이 낮다

• 가정환경

• 집값: 집값이 떨어지면 refinance가 어려워 조기상환이 감소한다

• 번아웃 효과: 과거에 갱신이 많이 된 모기지의 경우 이자율에 둔감하다
  refinancing의 이점을 이용할 수 있었던 사람들은 이미 이러한 이점을 이용하여 낮은 이자율을 통해
  계약을 유지하고 있을 것이며 남은 사람들만 refinance를 진행할 것이기 때문이다

✏️MBS

MBS의 가치를 결정짓는 중요 요인은 3가지다
만기의 가중 평균, 쿠폰의 가중 평균, 중도상환 속도

중도상환 속도의 측정치

• constant maturity mortality
  쿠폰 지급이후 모든 시점에서 상환된 확률이 p로 동일

p가 달별로 구해진 확률이기 때문에 연율하여 사용하려면 $(1-p)^12$이 되어야 하고
이를 $(1-CPR)$로 표현할 수 있다

CPR은 conditional prepayment rate의 약자

• PSA Experience
  100% PSA는 PSA에 의해 만들어진 산업 벤치마크 지수이다
  이는 조기상환 속도를 설명하며 몇 가지 가정을 가지고 있다

  CPR = 원금의 0.2%가 첫 달에 지불된다

  CPR 30개월간 매달 0.2%씩 증가합니다

  CPR은 만기까지 6%수준을 유지합니다

  이 방법은 조기상환의 양이 모기지 풀의 나이에만 의족하기 때문에 간단하다

Pass-Through

패스쓰루는 가장 간단한 MBS이다

주택 소유자로부터 받은 원리금을 일부 비용만 제외하고 투자자하게 직접 전달해주는 방식이다
이러한 구조는 투자자가 조기상환 위험에 노출되도록 한다

보통 이 pass-through의 쿠폰이 WAC보다 낮은데
둘의 차이 만큼이 쿠폰지급에 대한 신용을 확인하고 pool을 모아주는 MBS발행자에 대한 보상이다

패스스루의 가치를 계산하는 과정에 대해 알아보자

먼저 PSA 레벨이 주어지면 이를 통해 조기상환 확률을 구할 수 있다

이후 t시점에 가능한 현금흐름들을 살펴보자

모기지 이자: $I_t = {r\over 12}\times L_t$
예정된 원금: $Pay^{scheduled}=C_t-I_t$
조기상환 원금: $Pay^{prepaid}= p_t\times L_t$

그렇다면 1달 후의 현금흐름은 다음과 같을 것이다

미상환된 원금: $L_{t+1}=L_t-Pay^{scheduled}-Pay^{prepaid}$
예정된 쿠폰: $C_{t+1}=(1-p_t)\times C_t$

이때 패스스루의 현금흐름은 모기지 금리가 아닌 패스스루 금리에 영향을 받는다는 점을 고려해야 한다

패스스루 이자: $I_t^{PT} = {r^{PT}\over 12}\times L_t$

Total cash flow: $CF_t=I_t^{PT}+Pay^{scheduled}+Pay^{prepaid}$

이후 이를 현재가치할인하여 구하면 된다

이때 신용 위험이 0에 가깝기 때문에 Treasury discount curve를 이용해도 된다

패스스루의 Effective Duration

금리가 50bp움직일때 PSA가 반대로 50%p씩 움직인다면

$D \approx -{1\over P}{P(+50bps)-P(-50bps)\over 2\times 50bps}$

이 듀레이션은 effective duration이며 금리변화에 따라 PSA가 안 움직인다고 가정하여 구한 듀레이션보다 작다

따라서 금리 변화에 따른 중도상환 속도 변화를 고려해야한다

패스스루의 Negative Effective Convexity

중도상환의 두 번째 특징은 이자율과 관련하여 MBS 가격의 음의 볼록함을 유도하는 것이다

고정금리채권처럼 일반적으로 금리가 하락하면 가격이 상승한다

하지만 금리가 하락하면 조기상환률을 높이고 이 경우 가격이 그만큼 상승하지 못한다
즉, 음의 볼록성을 만들어 낸 것이다

금리가 낮을 때 금리 변동에 덜 민감한 반면, 금리가 높을 때 더 민감하다

또한 이를 설명하는 방법 중 하나로 다음을 생각해보자

디폴트 리스크가 거의 없음에도 국채보다 높은 수익률을 지니고 있는 이유가 무엇일까
이는 아메리칸 콜옵션처럼 금리가 낮아졌을 때 주택 소유자들이 이를 행사한다고 할 수 있다
그렇다면 패스스루를 구매한 투자자 입장에서는 이러한 옵션 프리미엄을 받아야 할 것이다

앞에서 양의 볼록성이 평균적으로 수익을 가져다주었다고 배웠다

따라서 반대로 음의 볼록성은 시간이 지남에 따라 이자율이 무작위로 움직이면 평균적으로 손해를 본다

그렇기 때문에 이에 대한 보상으로 높은 쿠폰 이자율이 필요로 하는 것이다

그렇다면 어떻게 이를 측정할 수 있을까?

effective convexity

$C \approx {1\over P}{P(+x\, bps)+P(-x\, bps) -2\times P\over (x\, bps)^2}$

TBA 시장

트레이더가 증권을 사려고 할 때 풀의 정확한 구성요소를 모르는 상태로 계약을 체결한다

풀은 이미 특정 가격에 팔렸기 때문에 세컨더리 마켓에서 모기지를 이러한 풀에 팔 수 있어
은행은 고정된 모기지 금리를 적용할 수 있다

이처럼 계약이 확정되고 풀이 공개 되며 이에 대한 현금흐름을 고정한다는 점에서 선도 거래로 생각할 수 있다

은행이 새로 돈을 빌리는 사람의 채무불이행 위험을 부담할 필요가 없다면 더 나은 모기지 금리를 제공할 수 있어 TBA시장의 유동성은 중요하다

따라서 TBA시장은 Ginnie Mae, Fannie Mae, Freddie Mac의 패스 스루 증권으로만 거래된다

✏️CMO

이는 조기상환 위험에 대하여 다양한 수준의 노출을 제공한다

이러한 수준은 듀레이션 이자율 민감성을 포함한 위험과 수익률 특성에 영향을 미친다

따라서 투자자는 자신의 선호에 따라 상품을 구매할 수 있고 유동성이 증가한다

CMO Sequential 구조

총 원금을 Tranche A, B, C와 같이 그룹으로 나눈다

Tranche에 해당하는 원금에 대한 고정 이자를 받고 순차적으로 원금을 지급받는다

때때로 'Tranche Z'라는 것이 발행되는데 Z는 zero를 나타내며 현금흐름이 없다는 것을 의미한다

이는 쿠폰을 받지 않으며 이러한 쿠폰은 축적되어 원금에 쌓인다

Tranche Z는 현금흐름을 다음 Tranche로 옮기면서 발행자가 조기상환 위험으로 인한 영향력을 줄이도록 도와주며
투자자에게는 마지막에 남은 모든 것을 가져가도록 한다

이러한 구조로 인하여 현금흐름이 결정되면 각 tranche의 가치를 계산할 수 있다
또한 각 tranche의 가치의 합은 pass-through MBS의 가치와 같다

이때 CMO에 주의할 점은 이러한 원금의 배분이 MBS의 이자율 변화에 대한 민감도를 크게 바꾼다는 것이다

후순위로 갈 수록 원금의 지급시점이 늦어지며 듀레이션이 길어진다

자동이전형 MBS는 tranche로 이루어진 포트폴리오이기에 각 듀레이션의 가중평균은 패스스루의 듀레이션과 같다

그리고 조기상환 속도가 다양한 tranche의 지급 기한에 영향을 준다

따라서 PSA가 감소하면 조기상환속도가 늦어졌다는 것을 의미하여 각 tranche의 듀레이션도 길어진다

CMO Planned Amortization Class

PAC또한 다양한 tranche를 가지고 있다
각 tranche는 발행자가 선택한 PSA수준에 따라 미리 정해진 스케쥴에 prepayment를 받는다

이렇게 선택된 벤치마크 PSA는 실제 prepayment보다 높거나 낮을 수 있기에
여기서 발생한 차이는 Companion Tranche에 흡수된다

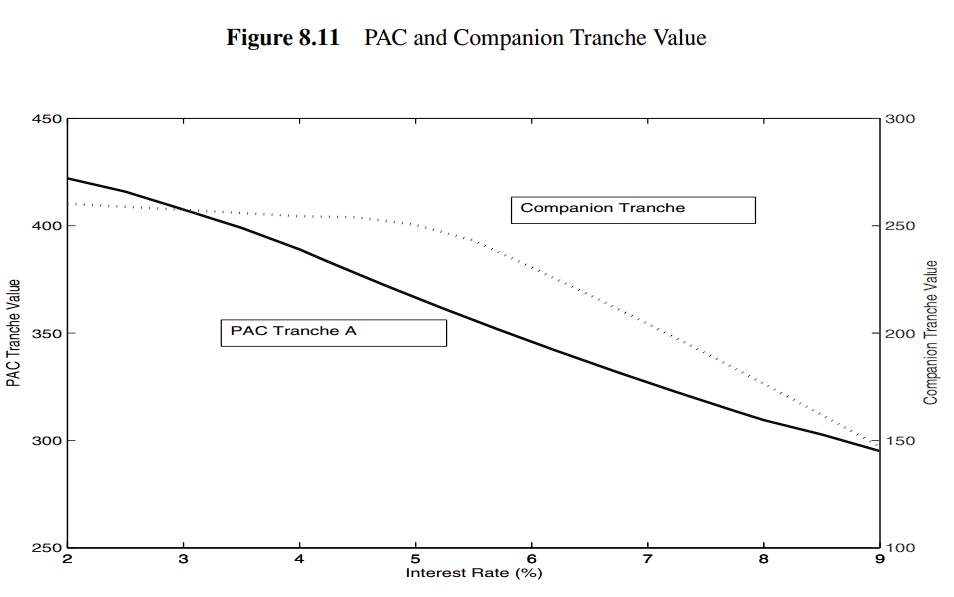
각 Tranche는 미래 현금 흐름이 확정되어 가격을 측정할 수 있다
대조적으로 Companion Tranche의 경우 조기상환 리스크를 모두 흡수함으로 가격이 조기상환에 큰 영향을 받는다

PAC가 작동하기 위해서 PSA의 상한선과 하한선을 먼저 정의한다

각 tranche에 대한 원금에 대하여 상한선과 하한선에 따라 예정된 지급액과 조기상환금이 책정된다

하한선을 가정했을때의 원금상환액과 상한선을 가정했을때의 원금상환액 중
작은액수를 기준으로 tranche에게 지급한다

Promised CF $C_t^{pac}=I_t+min(Pay_t^{hi,total}+Pay_t^{lo,total})$

따라서, Companion Trache CF $C_t^{Com}=C_t^{PT}-C_t^{pac}$ 이다

실제 PSA와 PAC의 현금흐름의 관계에 대해 알아보자

실제 PSA가 상한선과 하한선 내에서 움직인다면 현금흐름에 문제가 없을 것이다

하지만 금리가 매우 낮아져 상한선을 넘어서는 경우 Companion Tranche의 원금이 모두 상환될 것이다
따라서 PAC tranche는 PT와 같아져 조기상환 위험이 재발한다

이러한 이유로 매우 낮은 이자율구간을 제외하고는 PAC Tranche는 금리와 선형관계를 보인다
또한 Companion Tranche는 금리가 낮아질수록 가치가 constant해진다

IO와 PO Strips

IO와 PO는 현금흐름을 잘게 쪼개는 방법 중 하나이다

• IO: 이자만 지급, 금리가 낮아지고 조기상환이 발생하면 낮은 payment를 받는다
• PO: 원금만 지급, 금리가 낮아져 조기상환이 발생하면 PO에게 모두 전달된다

이제 조기상환 속도 변화에 따른 행동을 봐보자

이자율이 감소하여 PSA가 증가하면 IO 가치의 경우 상당히 감소한다
반대로 이 경우 total value가 높아지기 때문에 이를 보장하기 위해 PO의 가치는 증가한다

이러한 특징은 듀레이션에 영향을 미친다

IO의 듀레이션은 음수이며 상당히 작다
반면 PO의 듀레이션은 양수이며 크다

IO와 PO 듀레이션의 가중평균치가 본래의 pass-through 듀레이션과 같으니 당연한 이치이다