챕터9. ONE STEP BINOMIAL TREES

---

✏️ 1기간 이자율 이항 모형

이자율 모형은 단기 금리의 움직임을 명시함으로써 시작된다

이러한 움직임은 미래에 대한 예상이 담겨져 있으며

동시에 단기 금리를 통화 정책에 의해 결정되는 외생변수로 간주한다

(1기간을 6개월로 가정하고 예시를 든다)

이자율 이항 모형은 T-bond 뿐 아니라 다른 모든 금리 상품에 영향을 준다

모든 채권에 대하여 오직 단기 금리만이 중요한 역할을 한다고 가정하였기에

외생적으로 단기 금리가 변화한다면 모든 금리 상품은 종속적인 움직임을 보여준다

이러한 가정은 Fed의 바람일 것이지만 실제로 장기채의 경우 다른 변수들에도 영향을 받는다
하지만 차익거래 불가능 조건과의 관계를 찾기 위해 모형을 단순화 하려한다

Continuous Compounding

연속 복리 대신 6개월 복리 방식을 채택할 수 있을 것이다

하지만, 그럼에도 연속 복리를 사용하는 이유는 다음과 같다

• 어차피 연속 복리 이율을 이용하여 다른 이율을 계산할 수 있다

• 연속 복리를 사용할 경우 노드 사이의 기간을 조정할 수 있을 뿐더러 이에 따른 금리 자체도 바꿀 수 있다

• 많은 이자율 증권과 파생상품은 서로 다른 복리 빈도를 이용한 현금 흐름을 가지고 있다

✏️ 이항 모형에서의 No-arbitrage

복제 포트폴리오: 시점 $i=1$에서 금리가 올랐을 경우 가치 $V_{1,u}$, 떨어졌을 경우 가치 $V_{1,d}$를 가지는
포트폴리오를 만든 것, 따라서 시점 $i=0$에서 이 복제포트폴리오의 가치는 옵션의 가치와 같아야 한다
(No-arbitrage rule)

The Replicating Portfolio Via No Arbitrage

복제포트폴리오를 구성하기 위하여 N을 구하는 과정은 다음과 같다

payoff 시나리오를 생각한 뒤, 이와 같은 payoff가 나오는 복제 포트폴리오를 만든다

포트폴리오의 가치 $\Phi_{1,u} = N_1\times 100 + N_2\times P_{1,u}(2)=$ payoff $V_{1,u}$

포트폴리오의 가치 $\Phi_{1,d} = N_1\times 100 + N_2\times P_{1,d}(2)=$ payoff $V_{1,d}$

$N_2={V_{1,u}-V_{1,d}\over P_{1,u}(2)-P_{1,d}(2)}$

$N_1 = {1\over 100}\times [V_{1,u}-N_2\times P_{1,u}(2)]$

이는 금리 상품에서 끝이 아니라 채권 가격에 영향을 받는 상품에 대해서도 적용 가능하다

Where Is the Probability $p$?

지금까지 금리가 오를 가능성 $p$를 고려하지 않고 파생상품의 가격을 얻었다

그렇다면 옵션의 가격이 이러한 확률에 독립적이라는 것이 어떻게 가능할까?

금리가 오를 것이라는 기대감이 이미 채권의 가치에 내재되어 있기 때문에
옵션의 가격을 구할 때는 이를 고려하지 않아도 된다

✏️미래 현금 흐름의 현재 가치 할인을 통한 파생상품 Pricing

파생상품의 가격 결정을 위하여 우선 복제포트폴리오를 만들고 이 포트폴리오의 가치를 통해 가격을 얻었다

이 절에서는 좀 다른 방식의 가격 결정 방식을 소개한다

미래 현금 흐름을 위험 조정 현금 할인율을 통해 상각하여 파생상품의 가치를 얻는다

이자율 증권의 리스크 프리미엄

만기가 긴 채권의 경우 가격이 더 저렴하다
이유는 장기채에 리스크 프리미엄이 포함되어 있기 때문이다

미국채의 경우 디폴트 리스크는 거의 존재하지 않는다
하지만 금리가 상승하여 만기전에 채권이 판매된다면 자본 손실을 볼 수 있다

$Dollar\; risk\; premium\,=e^{-r_0\times \Delta}\times E[P_1(2)]-P_0(2)$

금리 위험의 시장 가격

파생상품들간의 관계를 설립할 것이다

${e^{-r_0\times \Delta}E[P_1(2)]-P_0(2)\over P_{1,u}(2)-P_{1,d}(2)}={e^{-r_0\times \Delta}E[V_1]-V_0\over V_{1,u}-V_{1,d}}$

• 좌변은 무이표채의 가격으로만 이루어진 반면 우변은 파생상품의 가경으로만 구성되어 있다

• 2기간이 만기인 무이표채에 대한 표현식은 우변의 파생상품에 대한 표현식과 같다

• 두 식의 분자는 리스크 프리미엄을 제외하고는 같다

• 분모는 두가지 시나리오에 대한 채권 혹은 파생상품의 위험을 나타낸다
  헤지를 위해서 상품과 이자율이 같이 가는지 반대로 가는지 알아야 한다(양수: 같은 방향, 음수: 반대 방향)

위의 식에 따라 이항모형에서 모든 금리 상품의 위험에 대한 리스크 프리미엄 비율은 $\lambda_0$로 같다

이때 람다를 모든 금리 상품에 공통적으로 아우르는 위험과 리스크 프리미엄에 대한 비율
즉, 위험의 시장 가격이라 한다

금리 상품 Pricing 공식

먼저 람다를 계산한다

$\lambda_0={e^{-r_0\times \Delta}E[P_1(2)]-P_0(2)\over P_{1,u}(2)-P_{1,d}(2)}$

이후 주어진 람다를 통해 파생 상품의 가치를 계산한다

$V_0=e^{-r_0\times \Delta}\times E[V_1] -\lambda_0 \times (V_{1,u}-V_{1,d})$

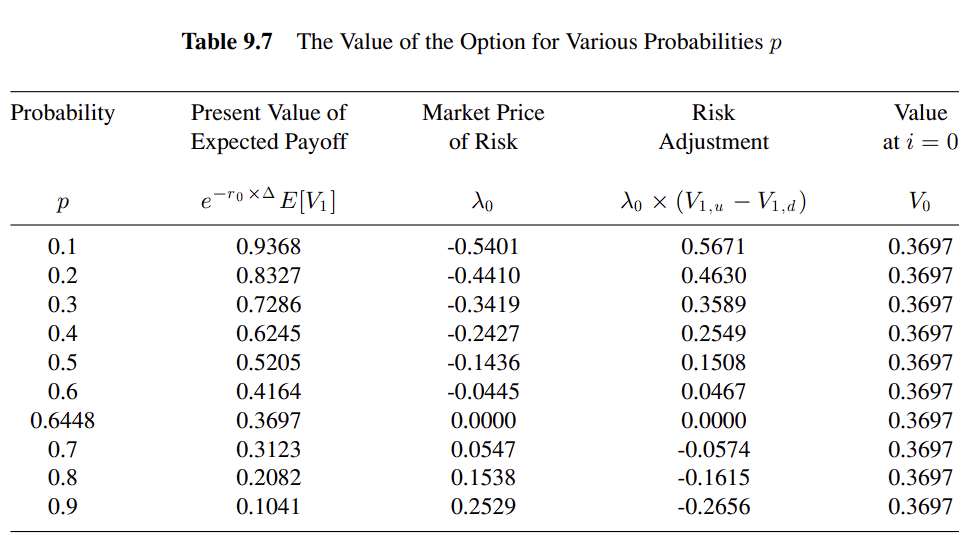
$p$를 모르면 어떻게 할까?

p를 잘 못 계산하더라도 금리 상품에 대한 가격 결정에는 영향을 미치지 않는다

하지만 핵심은 p를 잘못 구하면 람다(risk adjustment)를 잘못구하게 된다는 것이다

p가 증가할 경우 예상 payoff의 현재가치가 감소하지만 반대로 람다가 증가하여 상쇄된다

만기의 payoff가 정해진 상품으로부터 람다를 구했기 때문에 이러한 현상이 나타난다

✏️ 위험 중립 가격 결정

람다를 0으로 하는 특정 확률을 $p^*$이라 할 때 가격 결정 모형은 다음과 같다

$V_0=e^{-r_0\times \Delta}\times E^*[V_1]$

$E^*[V_1] = p^*\times V_{1,u}+(1-p^*)\times V_{1,d}$

이 때의 확률은 실제 확률과 다르며 이 확률을 적용함으로써 람다를 없애며 식을 간단하게 만들 수 있다

위험 중립 확률

$p^*={e^{r_0\times \Delta}P_0(2)-P_{1,d}(2)\over P_{1,u}(2)-P_{1,d}(2)}$

모든 금리 상품이 미래 기대 payoff의 현재가치에 의해 주어지며 이때 현재가치는 risk free rate에 의해 구해진다

금리 상품의 가격

위험 중립확률을 이용하여 valuation하는 방법은 다음과 같다

• 위험 중립 확률 계산

• $V_0=e^{-r_0\times \Delta}\times E^*[V_1]$에 의하여 계산

위험 중립 Pricing과 동적 복제

위험 중립 방법의 장점은 간단함이다

이때 시장 참여자들이 위험 중립적이라는 근본적인 가정이 없다는 것을 깨닫는 것이 중요하다

실제로 시장 참여자들은 장기채에 대하여 위험 프리미엄을 요구한다

위험 중립 방법은 단지 차익거래가 불가능하다는 명제를 이용하여 간단한 방식으로 가치를 구하는 것이다

이를 깨닫기 위해 중요한 것은 어떠한 두 상품 사이에 동적 복제 전략이 존재한다는 것이다

Risk Neutral Expectation of Future Interest Rates

위험 중립 확률하에 미래 기대 이자율(2.5234%)은 일반적인 기대 이자(2.17%)율 보다 높게 나온다

위험 중립 가격 결정은 올라갈 확률에 위험 프리미엄이 포함된 것에 버금간다

그렇다고 시장 참여자들이 금리가 2.5234%가 될 것이라고 기대하지 않는다

더 높은 기대 이자율이 나온 이유는 단지 시장 참여자들이 위험 상품을 지니며
요구하는 할인율이 더 높기 때문이다

이때 선도 이자율을 본다면 2.52%로 위험 중립 확률하에 기대 이자율과 매우 비슷하다

따라서 이는 선도 이자율이 시장의 미래 이자율에 대한 기대치와 같지 않기에
선도 금리를 미래 금리의 기대치로 생각하는 것에 주의가 필요하다는 거을 알려준다

높은 선도 금리는 두 가지를 의미(시장의 기대값이 높음, 위험에 대하여 더욱 회피적)

위험 중립 기대 금리와 배우 비슷하긴 하지만 정확히 같지 않다는 것을 보여준다

매우 비슷하지만 다른 이유는 위험 중립 가격 결정 방법이 동적 복제의 개념에 근거하기 때문이다

즉 동적 복제를 사용한 위험 중립 방법은 거래가 발생하는 가격이 중요시 여겨진다

더불어 금리는 가격과 볼록한 관계를 가지고 있기 때문에 기대 금리와 선도 금리는 차이가 난다

$f(0,1,2) < E^*[r_1]$

실제로도 2.52 < 2.5234