Cardinality : Example

STATS·2023년 7월 18일
해석개론
0

해석개론

목록 보기
3/4
post-thumbnail

Cardinality comparison of Even and N

We want to check if there bijective function exist such that f:{2n∣n∈N}→NLemma) If there exist bijective function g such thatg:N→{2n∣n∈N}, There also inverse of g exist, which is bijective function.Therefore if there exist such g, ∣{2n∣n∈N}∣=∣N∣Let g:N→{2n∣n∈N}, g(n)=2nI) Proof of Injectivityn1≠n2∈N⇒2n1≠2n2⇒g(n1)≠g(n2), ∴g is injective functionII) Proof of Surjectivity∀2n∈{2n∣n∈N},∃n∈N s.t g(n)=2n∴g is surjective function∴g is bijective, by lemma, so cardinality of to set is equal.\text{We want to check if there bijective function exist such that } \\ f:\{2n \lvert n \in \N\} \rightarrow \N \\ {} \\ \text{Lemma) If there exist bijective function g such that}\\ g: \N \rightarrow \{2n \lvert n \in \N\}, \ \text{There also inverse of g exist, which is bijective function.}\\ \text{Therefore if there exist such g, } |\{2n | n \in \N\}\rvert = \lvert \N \rvert \\{}\\ \text{Let } g:\N \rightarrow \{2n \lvert n \in \N\}, \ g(n) = 2n \\ {} \\ \text{I) Proof of Injectivity} \\ {} \\ n_1 \neq n_2 \in \N \Rightarrow 2n_1 \neq 2n_2 \Rightarrow g(n_1) \neq g(n_2),\ \\ \therefore \text{g is injective function} \\ {} \\ \text{II) Proof of Surjectivity} \\ {} \\ \forall 2n \in \{2n \lvert n \in \N\} , \exist n \in \N\ s.t \ g(n) = 2n \\ \therefore \text{g is surjective function} \\ {} \\ \\ {} \\ \therefore \text{g is bijective, by lemma, so cardinality of to set is equal.}

Cardinality comparison of Z and N

f:Z→N, f(z)={2z+1 (z≥0),−2z (z<0)Bacause f is bijective function, ∣Z∣=∣N∣f: \Z \rightarrow \N, \ f(z) = \begin{cases} 2z+1 \ (z \ge 0),\\ -2z \ (z < 0) \end{cases} \\ {} \\ \text{Bacause f is bijective function, } \lvert \Z \rvert = \lvert \N \rvert

Cardinality comparison of Q and N

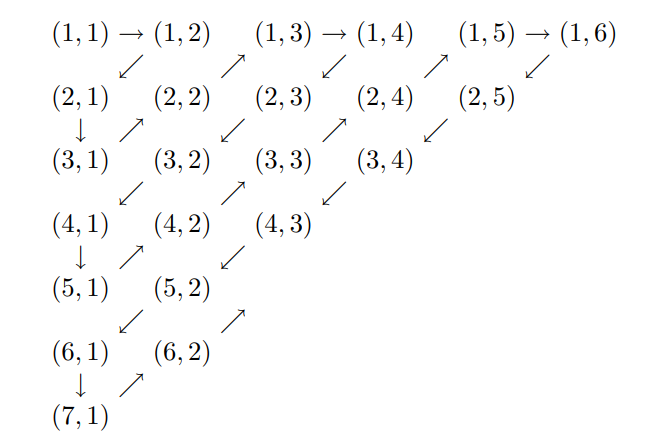
Lemma) ∣N∣=∣Q+∣proof)∣N∣=∣N2∣ since there exist bijection of "Zigzag" from N to N squared.Also, There exist bijection f:N2→Q+ such that: f(n1,n2)=n2n1∴∣N∣=∣N2∣, ∣N2∣=∣Q+∣⇒∣N∣=∣Q+∣Proof) since ∣Q−∣=∣Q+∣there bijection also exist from Q−to N. Let each bijection:g:Q+→N, h:Q−→NThen we can make bijection k:Q→Z such that: k(x)={0 (x=0)g(x) (x>0),−h(x) (x<0)∴∣Q∣=∣Z∣=∣N∣⇒∣Q∣=∣N∣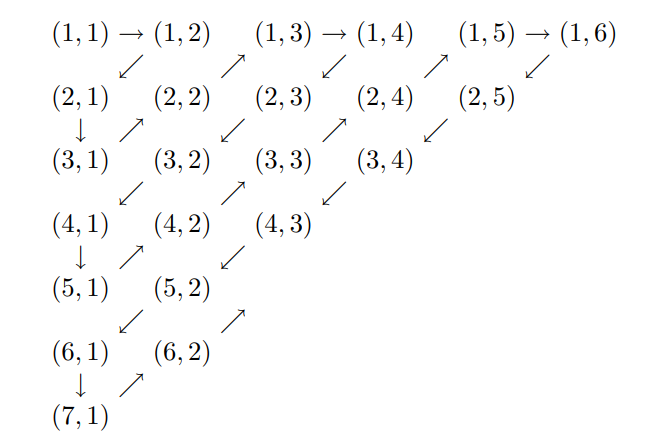Lemma) \ \lvert \N \rvert = \lvert Q^+ \rvert \\ {} \\ proof) \\ \lvert \N \rvert = \lvert \N^2 \rvert \ \text{since there exist bijection of "Zigzag" from N to N squared}. \\ \text{Also, There exist bijection } f: \N^2 \rightarrow Q^+ \text{ such that: } \\ f(n_1, n_2) = \frac{n_2}{n_1}\\ {} \\ \therefore \lvert \N \rvert = \lvert \N^2 \rvert, \ \lvert \N^2 \rvert = \lvert Q^+ \rvert \Rightarrow \lvert \N \rvert = \lvert Q^+ \rvert\\ {} \\ Proof) \ \text{since } \lvert Q^- \rvert = \lvert Q^+ \rvert \text{there bijection also exist from } Q^- \text{to N. Let each bijection:} \\ g:Q^+ \rightarrow \N, \ h: Q^- \rightarrow \N \\ {} \\ \text{Then we can make bijection } k: Q \rightarrow \Z \text{ such that: }\\ k(x) = \begin{cases} 0 \ (x=0) \\ g(x) \ (x > 0),\\ -h(x) \ (x < 0) \end{cases} \\ {} \\ \therefore \lvert Q \rvert = \lvert \Z \rvert = \lvert \N \rvert \Rightarrow \lvert Q \rvert = \lvert \N \rvert
profile
STATS
이전 포스트

Function, Cardinality : Definition

다음 포스트

완비성 공리

1개의 댓글

comment-user-thumbnail
happy
2023년 7월 18일

훌륭한 글이네요. 감사합니다.

답글 달기