Function, Cardinality : Definition

STATS·2023년 7월 17일
해석개론
0

해석개론

목록 보기
2/4

Function

Definition

집합 A,BA, B가 있을 때 AA의 모든 원소를 각각 BB의 유일하게 대응하는 규칙(사상)을 함수라고 하고, f:A→Bf : A \rightarrow B로 표기한다. 이 때 AA를 ff의 정의역, BB를 ff의 공역이라고 한다.

Image, Preimage

f:A→Bf : A \rightarrow B인 함수 ff를 정의하자.

Image

AA의 부분집합 CC가 있을 때,

f(C)={f(x)∣x∈C}⊂Bf(C) = \{f(x) | x \in C\} \subset B

를 ff에서의 CC의 상(Image)라고 한다.

Preimage

반대로 BB의 부분집합 DD가 있을 때

f−1(D)={x∈A∣f(x)∈D}⊂Af^{-1}(D) = \{x \in A | f(x) \in D\} \subset A

를 ff%에서의 $D의 역상(Preimage)라고 한다.

Injectivity, Surjectivity, Bijectivity

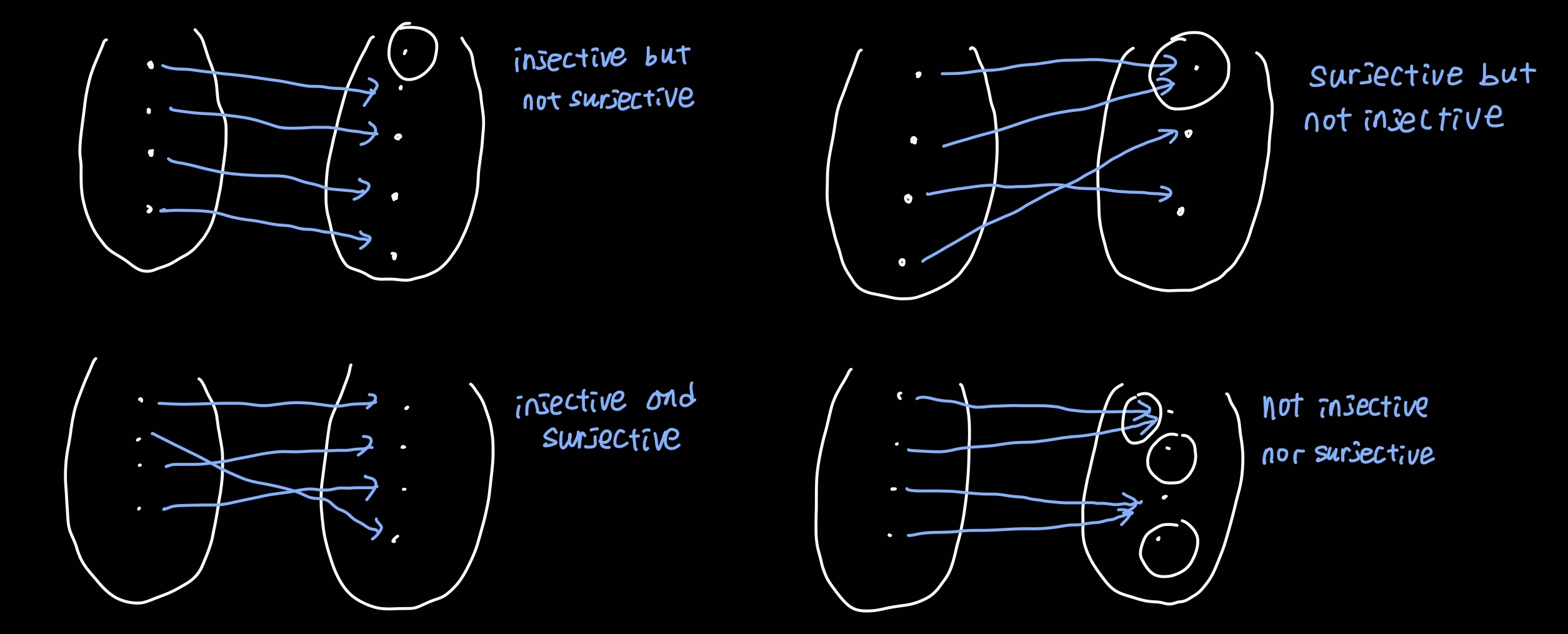
Injectivity

ff가 다음을 만족하면 ff를 Injective function(단사 함수) 또는 one-to-one function이라고 한다.

∀x1,x2∈A,f(x1)=f(x2)⇒x1=x2≡∀x1,x2∈A,x1≠x2⇒f(x1)≠f(x2)\forall x_1, x_2 \in A, f(x_1) = f(x_2) \Rightarrow x_1 = x_2 \\ {} \\ \equiv \forall x_1, x_2 \in A, x_1 \neq x_2 \Rightarrow f(x_1) \neq f(x_2)

Surjectivity

ff가 다음을 만족하면 ff를 Surjective function(전사 함수) 또는 on-to function이라고 한다.

f(A)=Bf(A) = B

Bijectivity

만약 ff가 Injective function이고 Surjective function이면 Bijective function(전단사 함수)라고 한다.

Composite Function, Inverse Function

Composite Function

f:A→Bf: A \rightarrow B, g:B→Cg: B \rightarrow C인 함수들이 있다고 하자. 이 때 합성함수 g∘fg ∘f 를 다음과 같이 정의한다.

g∘f:A→C,∀x∈A,(g∘f)(x)=g(f(x))g ∘f:A \rightarrow C, \forall x \in A, (g∘f)(x) = g(f(x))

Inverse Function

f:A→Bf : A \rightarrow B가 전단사함수일 때, ff의 역함수 f−1f^{-1}을 다음과 같이 정의한다.

f−1:B→A,∀x∈A,f−1(f(x))=x∀y∈B,f(f−1(y))=yf^{-1} : B \rightarrow A, \\ {} \\ \forall x \in A, f^{-1}(f(x)) = x \\ {} \\ \forall y \in B, f(f^{-1}(y)) = y

ff가 전단사함수면 f−1f^{-1}도 전단사함수라는 특징을 가진다.

We want to show f−1 is bijective function∀y1,y2∈B,f−1(y1)=f−1(y2)⇒f(f−1(y1))=f(f−1(y2))⇒y1=y2∴f−1 is injective function∀x∈A,∃f(x)∈B s.t f−1(f(x))=x∴f−1 is surjective functiontherefore f−1 is bijective function\text{We want to show } f^{-1} \text{ is bijective function} \\ {} \\ \forall y_1, y_2 \in B, f^{-1}(y_1) = f^{-1}(y_2) \Rightarrow f(f^{-1}(y_1)) = f(f^{-1}(y_2)) \Rightarrow y_1 = y_2 \\ {} \\ \therefore f^{-1} \text{ is injective function} \\ {} \\ {} \\ \forall x \in A, \exists f(x) \in B \ s.t \ f^{-1}(f(x)) = x \\ {} \\ \therefore f^{-1} \text{ is surjective function} \\ {} \\ \text{therefore } f^{-1} \text{ is bijective function}

Cardinality

기수(Cardinality)는 집합의 크기를 나타내는 측도다. 기수는 다른 집합과 집합의 크기를 비교할 때 자주 사용된다.

기수의 특이한 점은 두 집합의 크기를 비교할 때, 원소들을 서로 짝짓는 방법을 이용한다는 점이다. 만약 두 집합끼리 모든 원소를 하나씩 짝지을 수 있다면 두 집합의 크기는 같다고 할 수 있다.

Comparision of Cardinality

A,BA, B 두 집합의 원소를 하나씩 모두 짝지을 수 있다는 것은 AA에서 BB로 가는 전단사 함수가 존재한다는 것을 의미한다.

Equality of Cardinality

∃ bijective function f:A→B⇒∣A∣=∣B∣≡∣B∣=∣A∣  (∵f−1 is bijective)\exist \ bijective \ function \ f: A \rightarrow B \Rightarrow \lvert A \rvert = \lvert B \rvert \equiv \lvert B \rvert = \lvert A \rvert \ {} \ (\because f^{-1} \ is \ bijective)

Inequality of Cardinality

∃ injective function f:A→B⇒∣A∣≤∣B∣if ∣A∣≤∣B∣ but ∣A∣≠∣B∣⇒∣A∣<∣B∣\exist \ injective \ function \ f: A \rightarrow B \Rightarrow \lvert A \rvert \le \lvert B \rvert \\ {} \\ if \ \lvert A \rvert \le \lvert B \rvert \ but \ \lvert A \rvert \neq \lvert B \rvert \Rightarrow \lvert A \rvert < \lvert B \rvert

Comparision on three sets

∣A∣=∣B∣, ∣B∣=∣C∣⇒∣A∣=∣C∣Proof)∣A∣=∣B∣⇒∃ bijective function f:A→B∣B∣=∣C∣⇒∃ bijective function g:B→CWe want to show g∘f:A→C is bijective function.∀x1≠x2∈A⇒f(x1)≠(x2)⇒g(f(x1))≠g(f(x2))∴g∘f is injective functionf(A)=B⇒g(B)=C=g(f(A))∴g∘f is surjective function∴∃ bijective function g∘f:A→C⇒∣A∣=∣C∣\lvert A \rvert = \lvert B \rvert, \ \lvert B \rvert = \lvert C \rvert \Rightarrow \lvert A \rvert = \lvert C \rvert \\ {} \\ Proof) \\ \lvert A \rvert = \lvert B \rvert \Rightarrow \exists \ bijective \ function \ f: A \rightarrow B \\ {} \\ \lvert B \rvert = \lvert C \rvert \Rightarrow \exists \ bijective \ function \ g: B \rightarrow C \\ {} \\ \text{We want to show } g ∘f : A \rightarrow C \text{ is bijective function.} \\ {} \\ \forall x_1 \neq x_2 \in A \Rightarrow f(x_1) \neq (x_2) \Rightarrow g(f(x_1)) \neq g(f(x_2)) \\ \therefore g∘f \ is \ injective \ function \\ {} \\ f(A) = B \Rightarrow g(B) = C = g(f(A)) \\ \therefore g∘f \ is \ surjective \ function \\ {} \\ \therefore \exist \ bijective \ function \ g ∘ f : A \rightarrow C \Rightarrow \lvert A \rvert = \lvert C \rvert

Hierarchy of sets

Definition of Finity of set

∃ n∈N s.t ∣A∣=∣{1,2,...,n}∣⇒A is finite set, ∣A∣=nA is infinite set if A is not finite set\exist \ n \in \N \ s.t \ \lvert A \rvert = \lvert \{1, 2, ..., n\}\rvert \Rightarrow \text{A is finite set, }\lvert A \rvert = n \\ {} \\ \text{A is infinite set if A is not finite set}

Definition of Countability set

∣A∣=∣N∣⇒A is countably infinite setA is finite set or countably infinite set⇒A is countable setA is uncountable set if A is not countable set\lvert A \rvert = \lvert \N \rvert \Rightarrow \text{A is countably infinite set} \\ {} \\ \text{A is finite set or countably infinite set} \Rightarrow \text{A is countable set} \\ {} \\ \text{A is uncountable set if A is not countable set}

profile
STATS
이전 포스트

Well ordering principle, Induction

다음 포스트

Cardinality : Example

2개의 댓글

comment-user-thumbnail
이태균
2023년 7월 18일

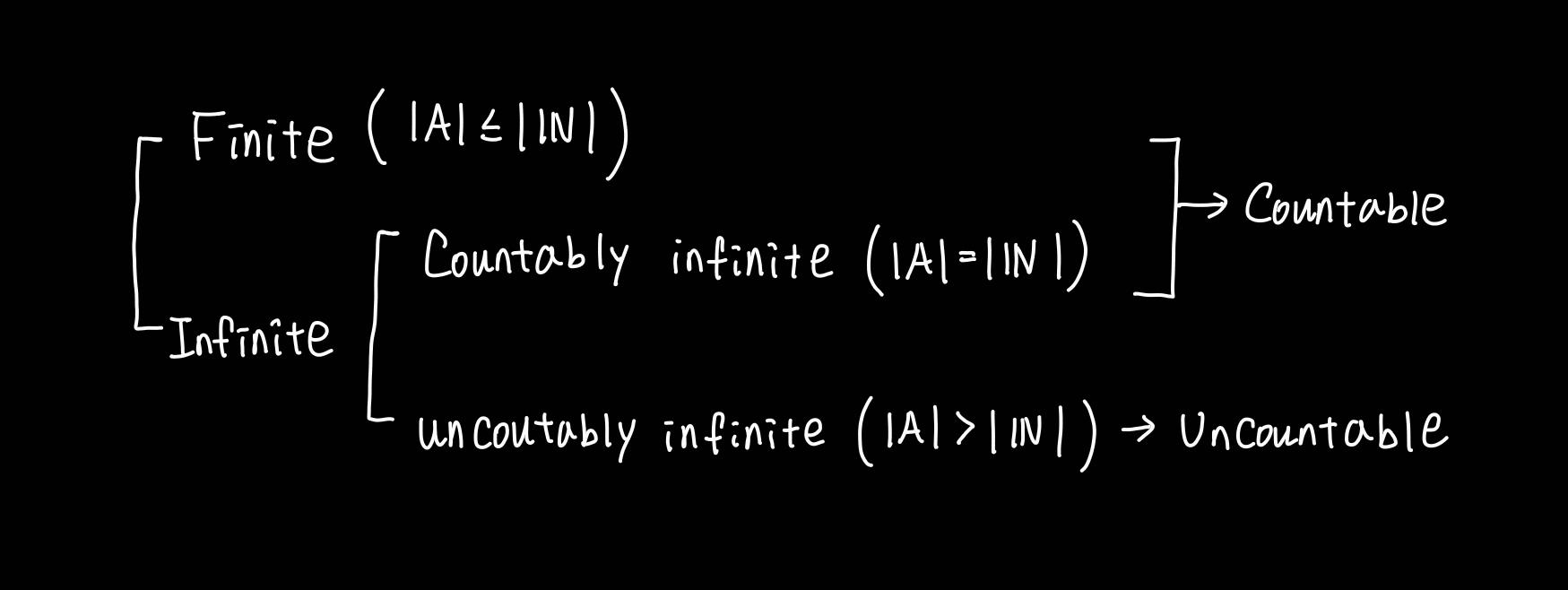
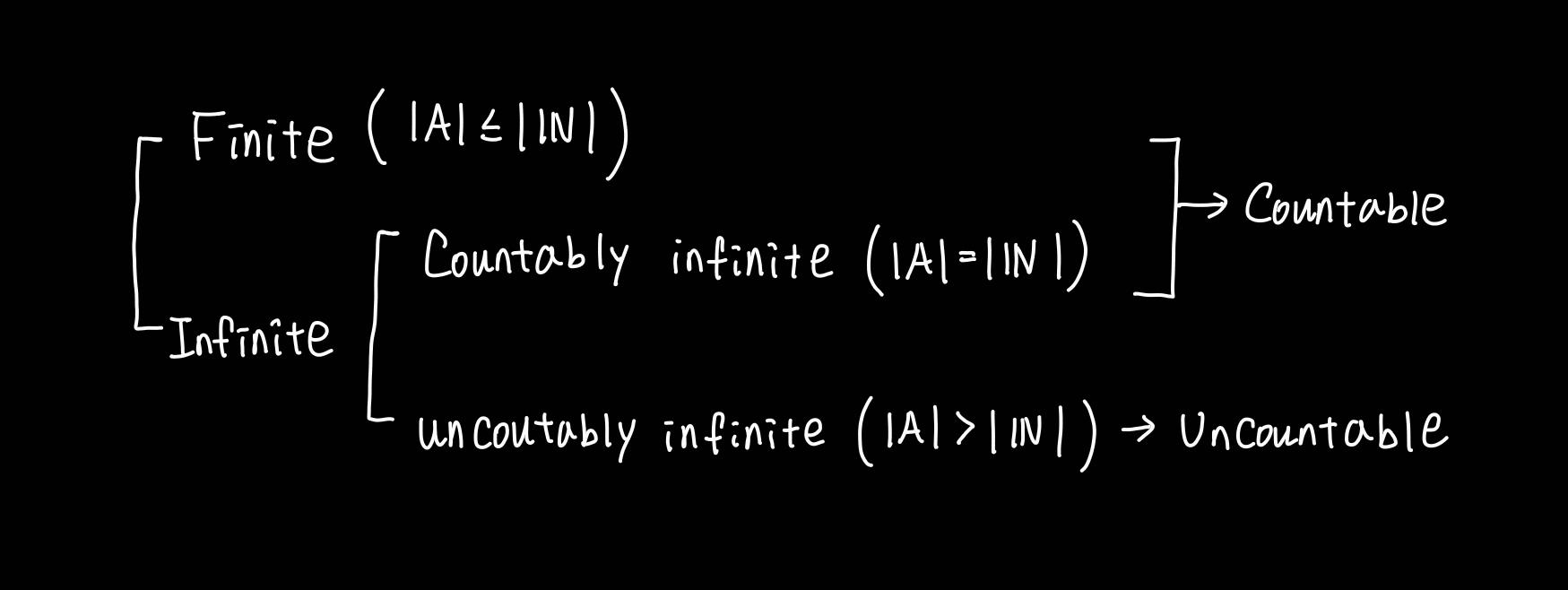
많은 도움이 되었습니다, 감사합니다.

답글 달기
comment-user-thumbnail
이태균
2023년 7월 18일

정말 좋은 정보 감사합니다!

답글 달기