해석개론
1.Well ordering principle, Induction

Well ordering Principle 집합 $S$가 $S \subset \N$, $S \ne \empty$일 때, $S$는 최솟값을 원소로 포함한다. $$ S \subset \N, \ S \ne \empty \Rightarrow \exist x \in S, \f
2023년 7월 16일
2.Function, Cardinality : Definition
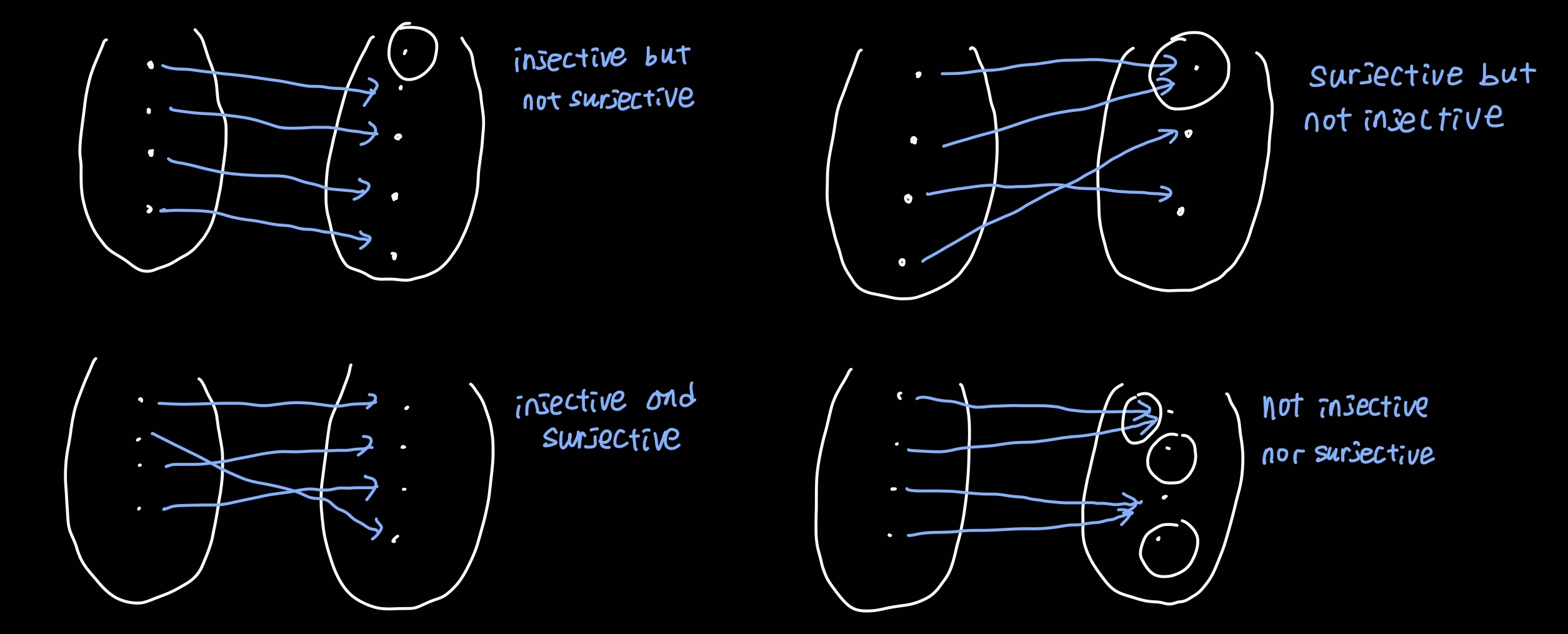
집합 $A, B$가 있을 때 $A$의 모든 원소를 각각 $B$의 유일하게 대응하는 규칙(사상)을 함수라고 하고, $f : A \\rightarrow B$로 표기한다. 이 때 $A$를 $f$의 정의역, $B$를 $f$의 공역이라고 한다.$f : A \\rightarrow
2023년 7월 17일
3.Cardinality : Example
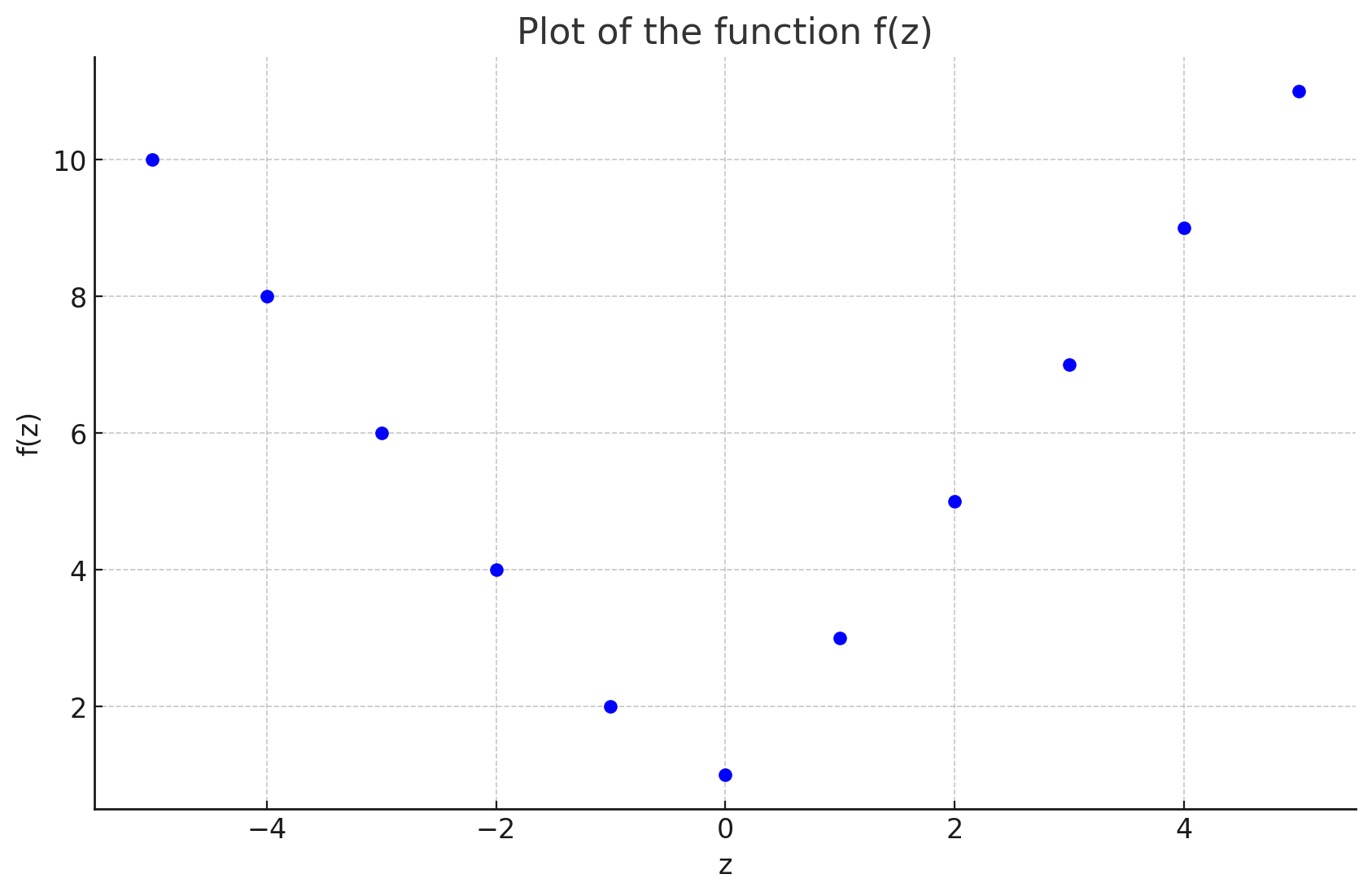
$$\\text{We want to check if there bijective function exist such that } \\ f:{2n \\lvert n \\in \\N} \\rightarrow \\N \\ {} \\ \\text{Lemma) If there
2023년 7월 18일
4.완비성 공리

상계, 하계 상한, 하한 최소값, 최대값 실수의 완비성 공리 예시
2023년 7월 21일