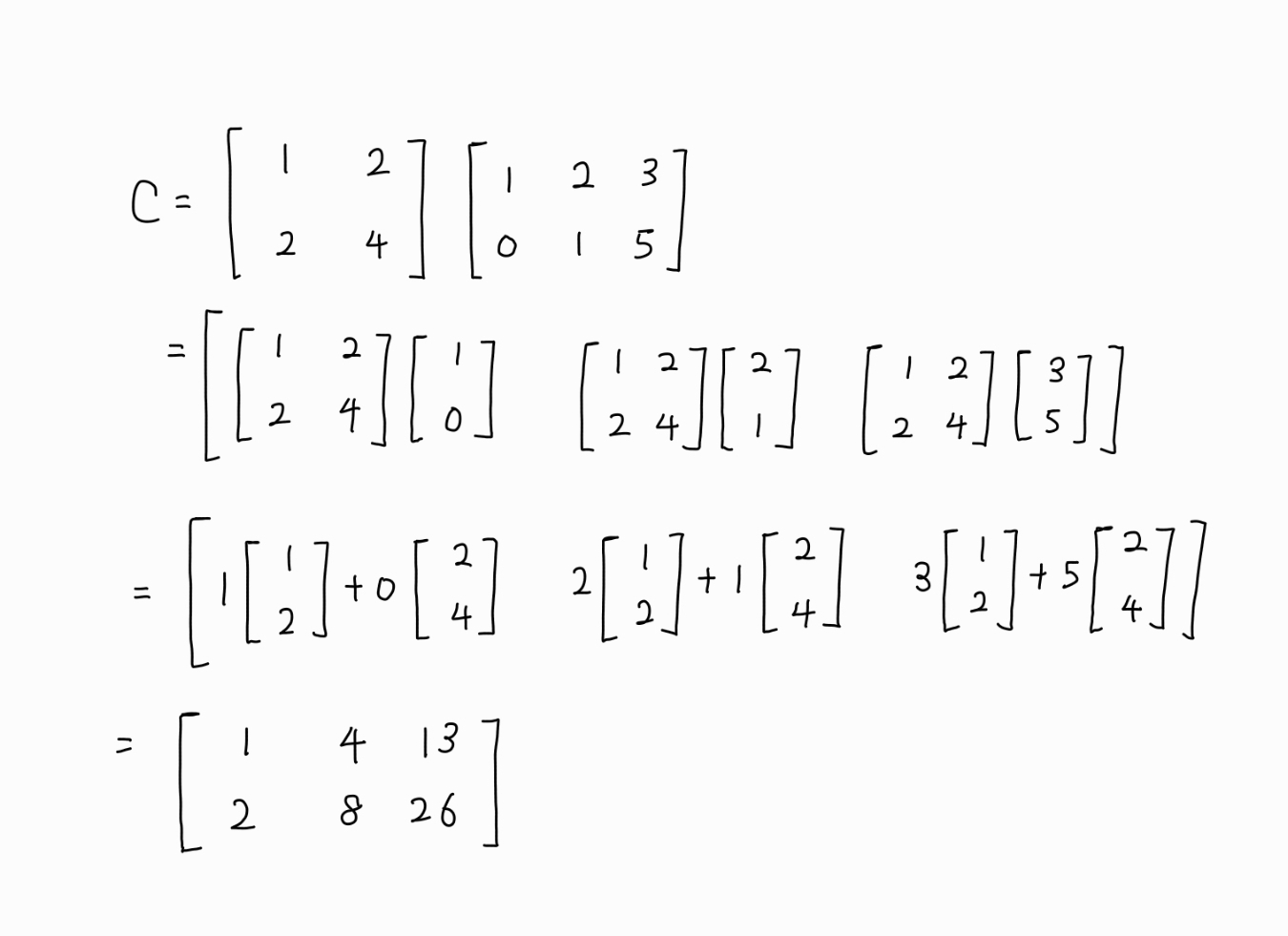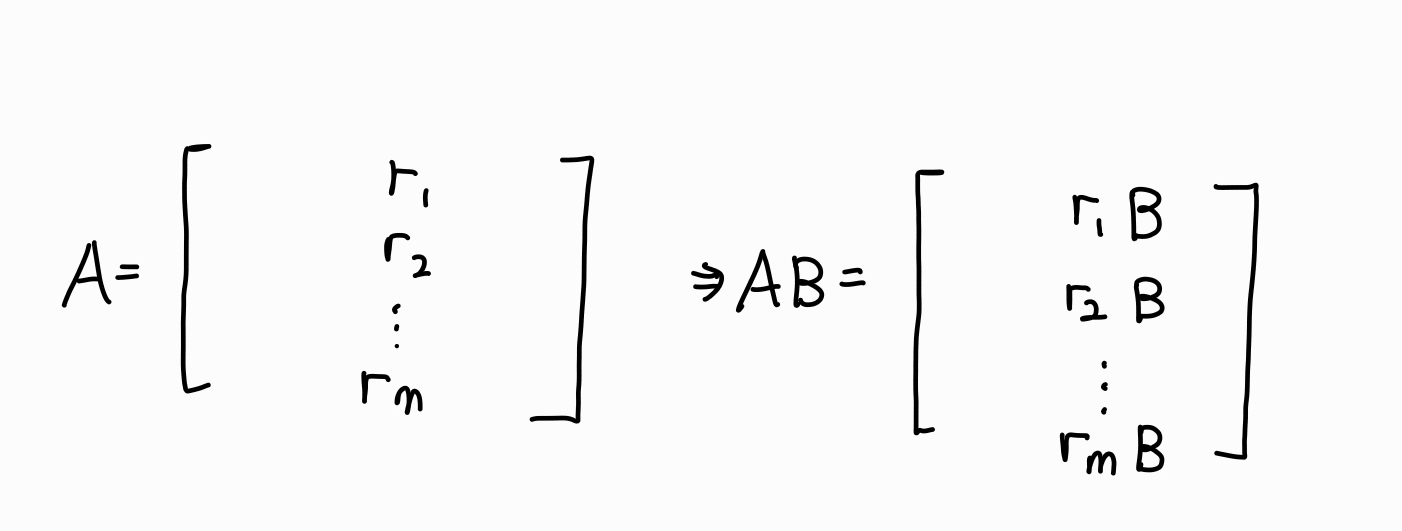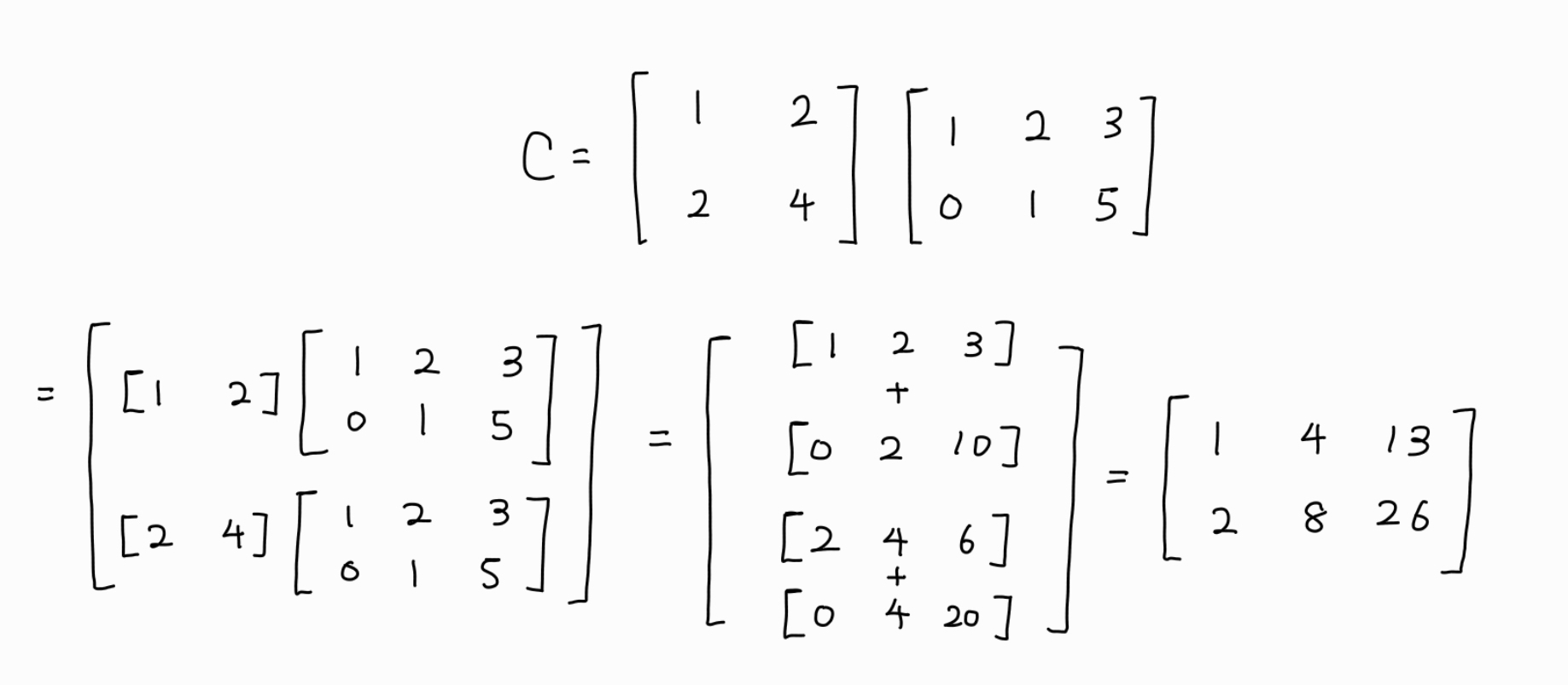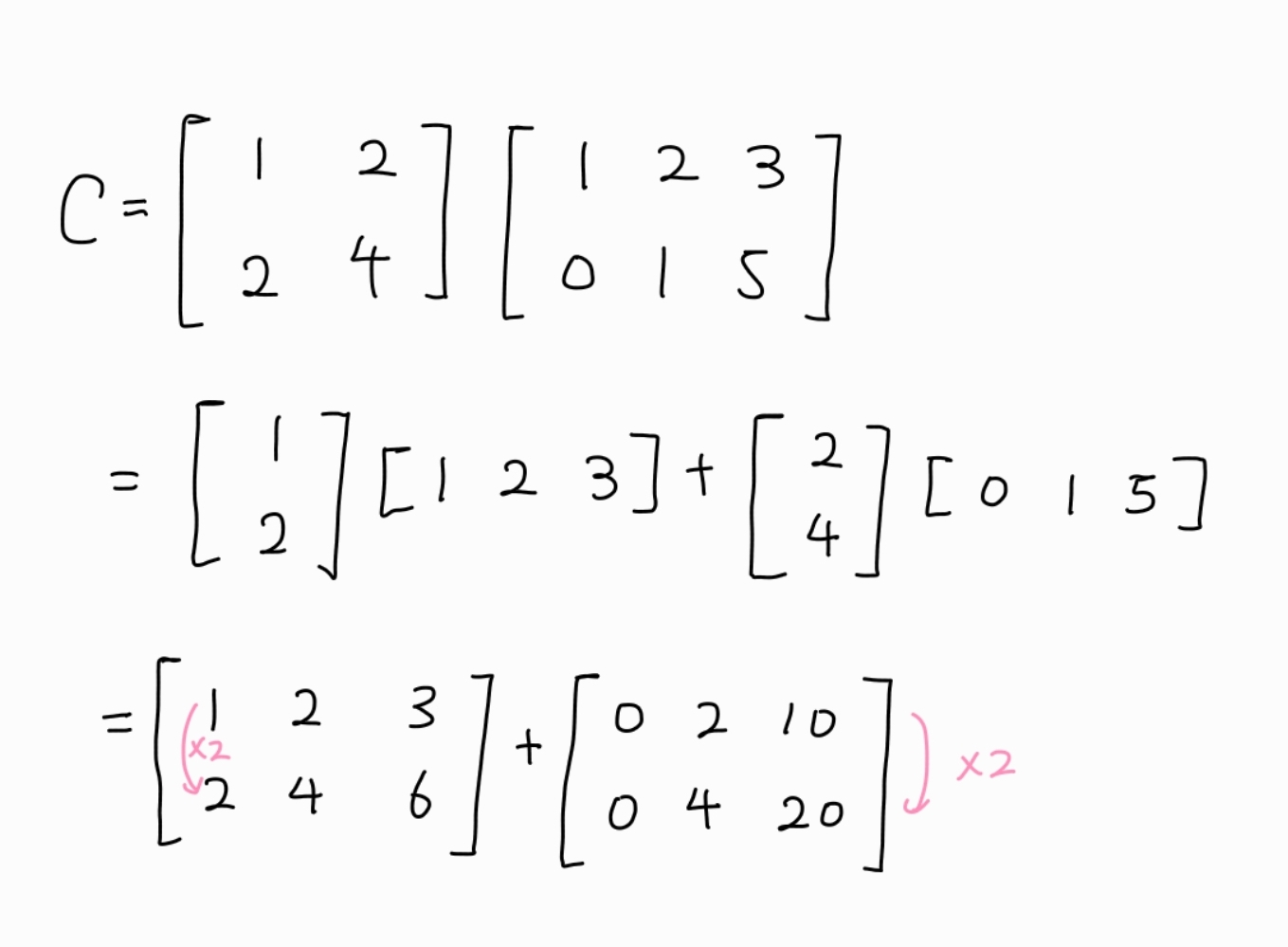Lecture 3

행렬 곱의 여러 관점

행렬 $A, B$가 각각 $m \times n$, $n \times p$의 행렬이라고 하자.
행렬 $C = AB$는 $m \times p$의 행렬이다. $AB$라는 행렬 곱은 관점에 따라 서로 다른 해석이 가능하다.

일반적 정의

행렬 $C$의 원소 $C_{ij}$는 $A$의 i번째 행과 $B$의 j번째 열의 내적으로 계산한다.

열의 관점

B를 열벡터들로 나타내면 $B = [b_1\ b_2 \ ... \ b_p]$로 나타낼 수 있다.
이 때 $C$는 다음과 같이 표현 가능하다.

즉 $C$의 각 열은 $A$와 $B$의 각 열의 곱으로 계산된다. 이 경우 행렬과 행렬의 곱은 각 열에서 행렬과 벡터의 곱으로 표현된다.

따라서 $C$의 각 열은 $b_j$를 결합의 계수들로 하여 $A$의 각 열벡터를 선형 결합한 것이다.
$b_j$를 결합의 계수로 한다는 것은 $b_j$의 원소들이 $A$ 열벡터 각각의 가중치 역할을 한다는 것이기도 하다.

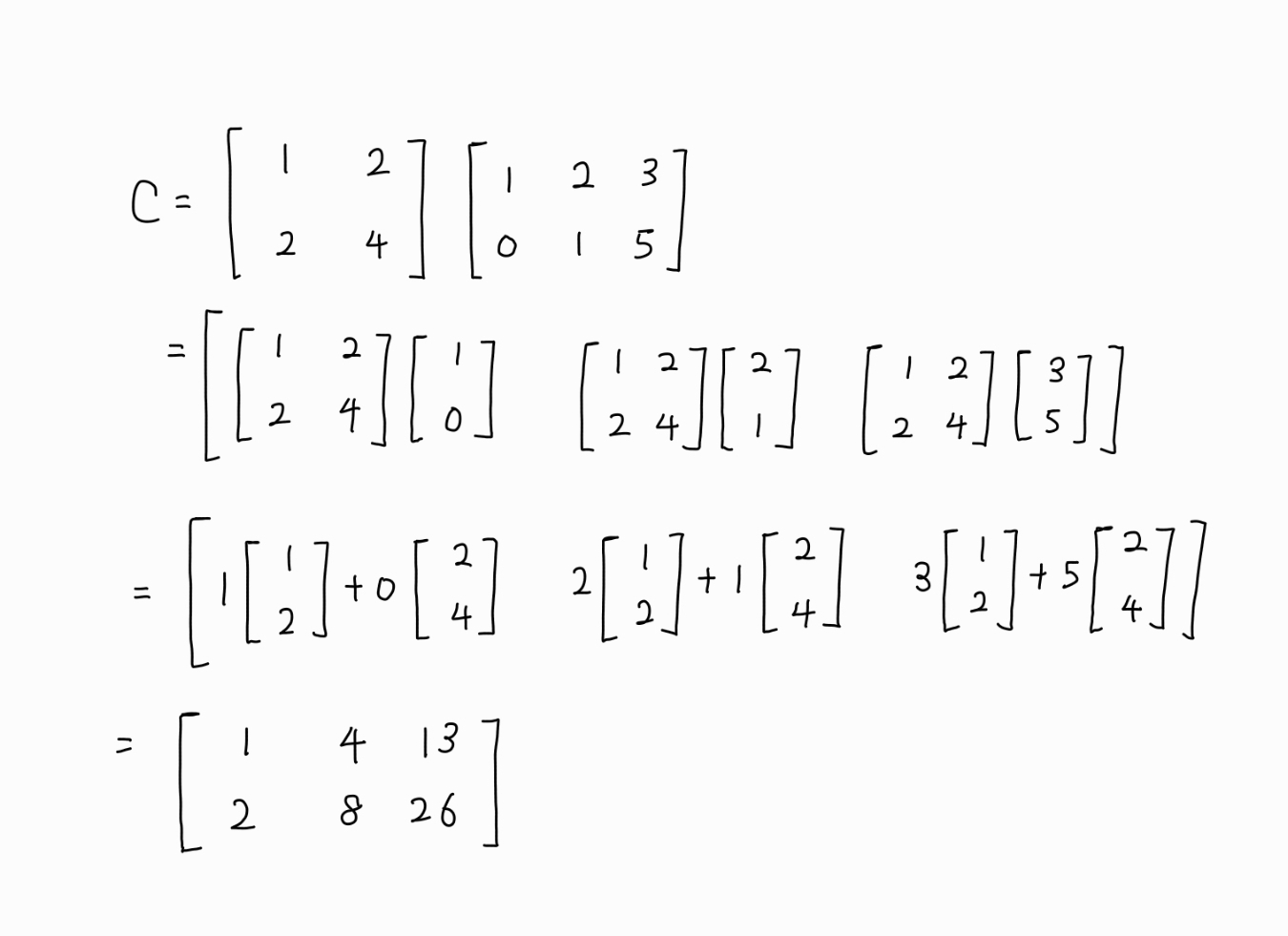
행의 관점

행의 관점도 열의 관점과 비슷한 논리로 전개한다.

A를 행벡터들로 나타내면 $C= AB$의 각 행은 A의 행벡터와 B를 곱한 것과 동일하다.

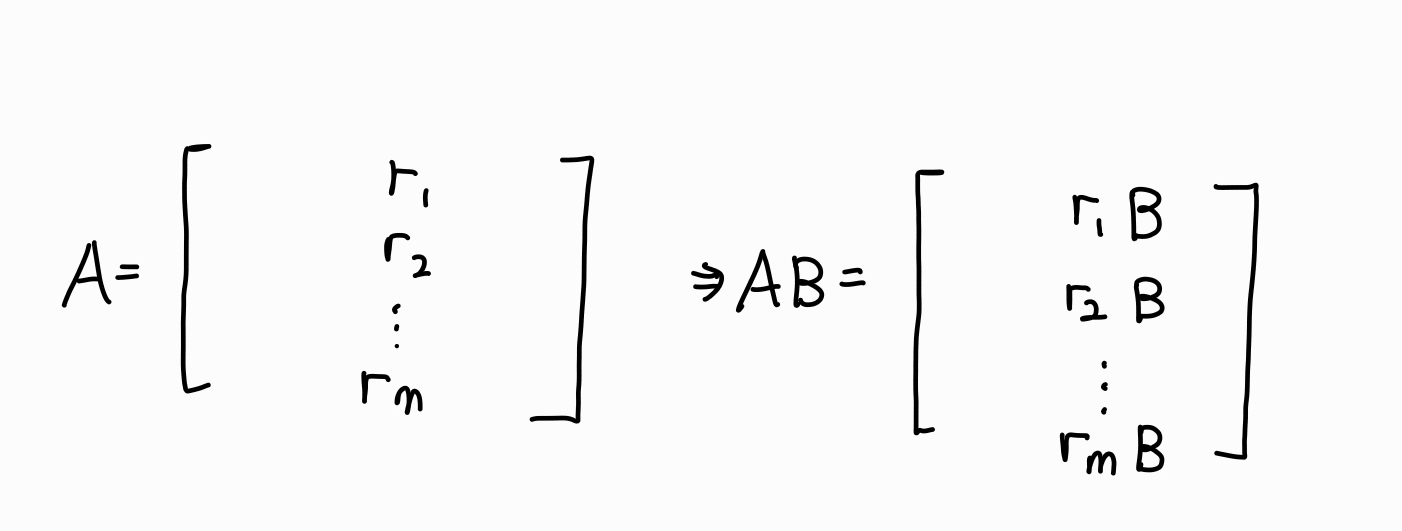
열의 관점에서는 B의 열벡터가 $A$의 열벡터의 선형 결합의 계수 역할을 했다면, 행의 관점에서는 A의 행벡터가 $B$의 행벡터의 선형 결합의 계수 역할을 한다.

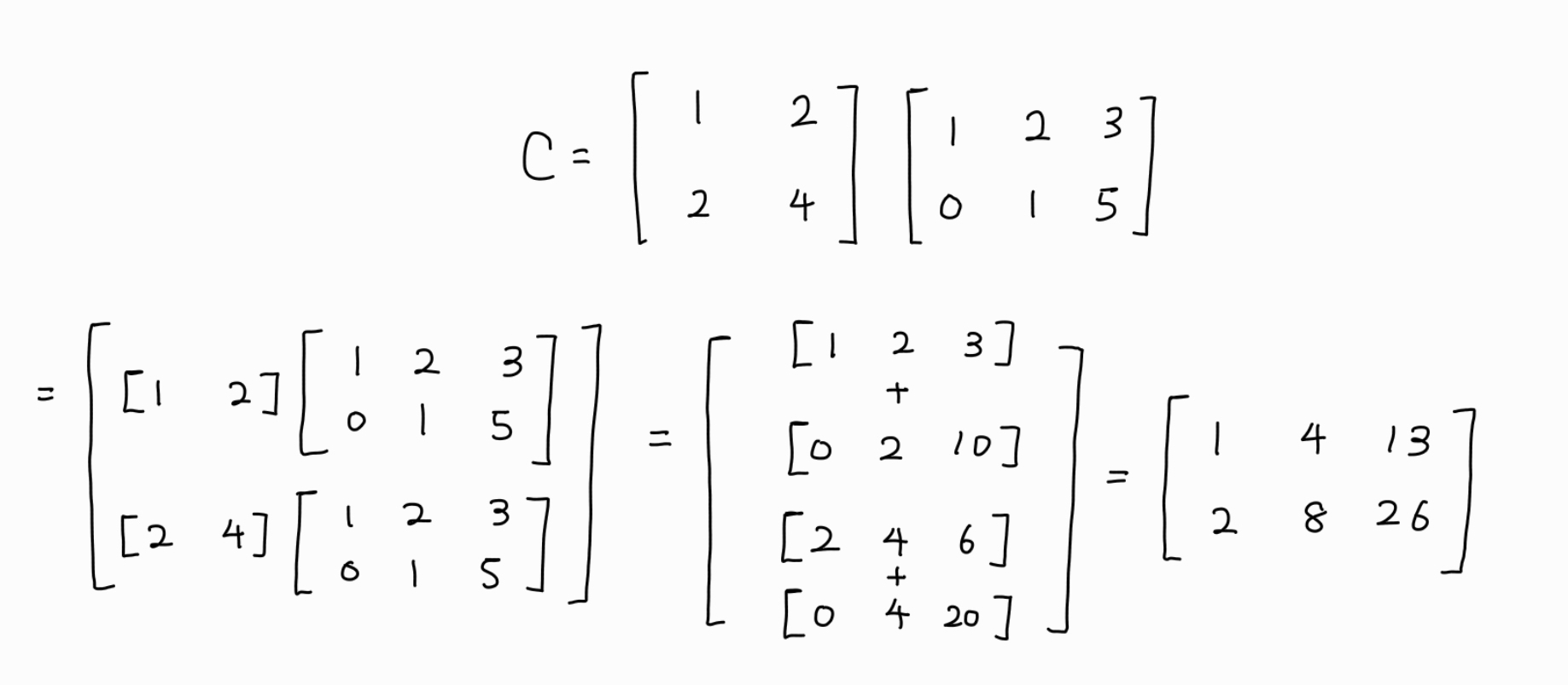
Rank 1 Matrix

$C = AB$에서, A의 각 열벡터는 $m \times 1$이고 B의 각 행벡터는 $1 \times p$의 벡터이다. 따라서 A의 열벡터와 B의 행벡터를 곱하면 $m \times p$가 되는데, 이를 이용해 행렬곱을 다음과 같이 표현할 수도 있다.

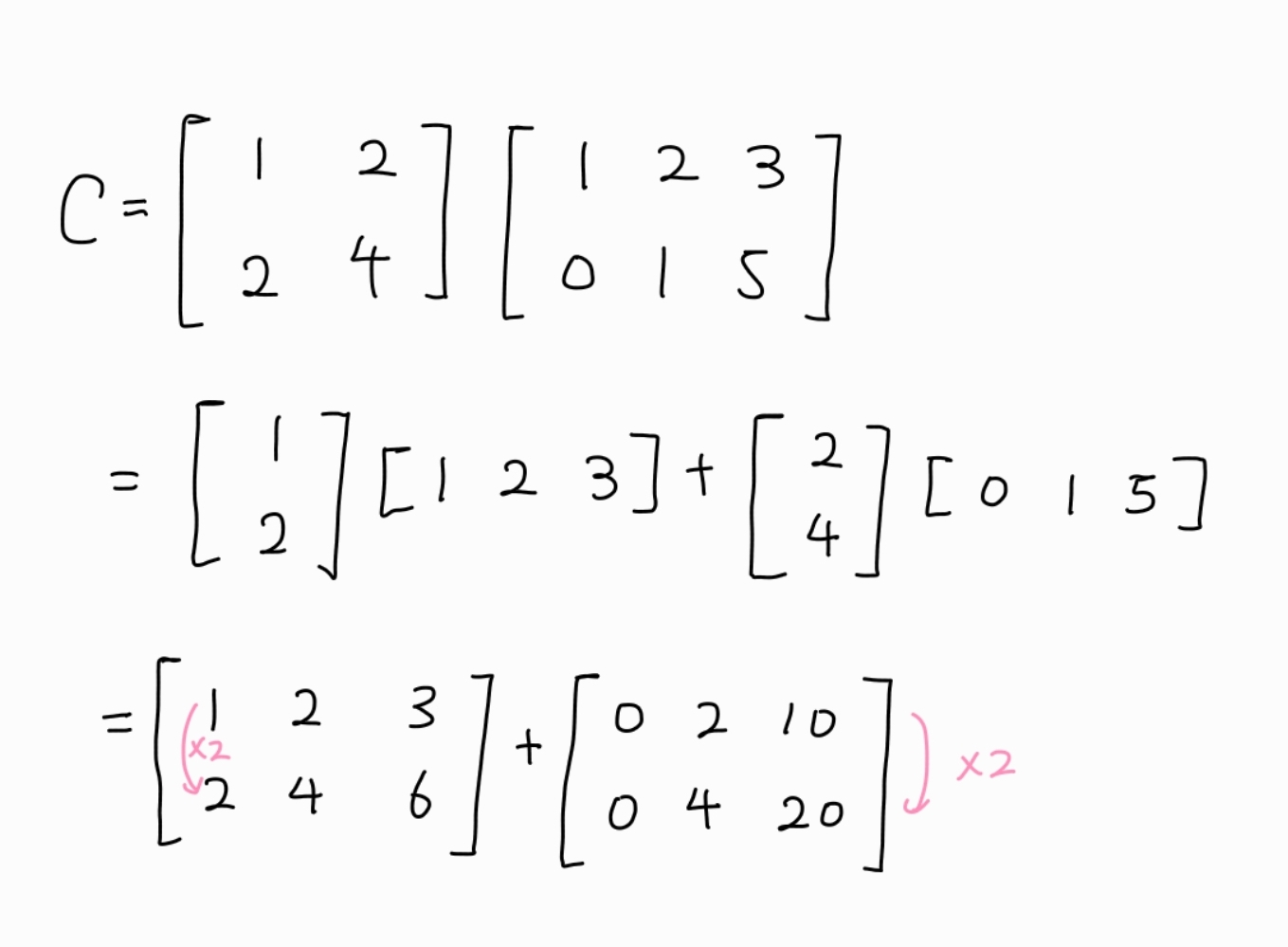
특이한 점은 덧셈의 피연산자인 각 행렬의 모든 행/열이 상수배 관계로 나타나 Rank 1 행렬이 된다.

각 행렬은 A의 열벡터와 B의 행벡터를 곱해 만들어지므로, 행렬의 곱 중 행의 관점에서 볼 때 결과 행렬은 동일한 행에 다른 상수만 곱한 것이 되기 때문이다.

역행렬

$A$가 $n \times n$의 정방행렬일 때, A의 역행렬 $A^{-1}$이 존재한다면 A는 가역행렬이라고 하고 다음을 만족한다.

역행렬을 찾는 방법

행렬 $A$가 위와 같을 때, A의 역행렬은 다음을 만족한다.

위에서 살펴 본 행렬 곱의 열의 관점에서 살펴보면, 문제를 다음과 같이 바꿀 수 있다.

따라서 두 선형계의 해는 각각 역행렬의 열벡터에 대응한다.

선형계들의 해를 구하려면 가우스-조던 소거법을 이용해야 한다. 그런데 두 선형계의 계수 행렬이 동일하므로 첨가행렬을 아래와 같이 설정하면 각 선형계의 해를 동시에 구할 수 있다.

좌측 계수 행렬을 기약행사다리꼴로 만들면 다음과 같다.

이 때 우변의 행렬이 $A$의 역행렬이 된다.

원리

처음의 첨가 행렬은 $[A | I]$로 나타낼 수 있다.
그리고 가역행렬 $A$를 기약행사다리꼴로 만든다는 것은 곧 $A$를 $I$의 형태로 만든다는 의미인데, $A$를 $I$로 만드는 과정은 기본 행 연산으로 이루어지므로 다음과 같이 표현할 수 있다.

$A$의 역행렬의 정의가 $A^{-1}A = I$를 만족하는 $A^{-1}$이었으므로, $E'$가 $A$의 역행렬이 된다는 것을 확인할 수 있다.

만약 $A$와 $I$에 동시에 $E'$에 대응하는 기본 행 연산을 진행하면 결과는 다음과 같다.

따라서 $A$를 $I$의 꼴로 만드는 과정을 $I$에 동일하게 적용하면 $A$의 역행렬이 된다.

역행렬이 존재하지 않는 경우

$A$에 대해 $Ax=0$을 만족하는 0이 아닌 벡터 $x$가 존재한다면 $A$는 역행렬이 존재하지 않는다.