선형대수학
1.벡터 공간

체 F에서의 벡터 공간 V는 다음 10가지 공리를 만족하는 합과 스칼라 곱 연산을 가지는 집합이다.
2.부분공간

F-벡터공간 $V$의 부분집합 $W$가 $V$의 합과 스칼라 곱 연산을 가진 F-벡터공간이면 $W$를 $V$의 부분공간이라고 한다.$W$가 벡터공간이 되기 위해서는 벡터공간의 공리들을 모두 만족해야 하는데, $W$가 $V$의 부분집합이라는 속성에 의해 대부분의 공리는
3.Lecture 1

여러 개의 선형방정식계가 모여 계를 이루는 것을 선형방정식계라고 한다.선형계의 해는 선형계에 속하는 각각의 방정식을 모두 만족시키는 해를 의미한다.선형방정식계는 계수 행렬과 미지수 벡터의 곱 그리고 상수 벡터로 나타낼 수 있다.$$2x-y = 0 \\\-x + 2y =
4.Lecture 3

행렬 곱의 여러 관점 행렬 $A, B$가 각각 $m \times n$, $n \times p$의 행렬이라고 하자. 행렬 $C = AB$는 $m \times p$의 행렬이다. $AB$라는 행렬 곱은 관점에 따라 서로 다른 해석이 가능하다. 일반적 정의 $$ C{ij}
5.Subspace, Column space

벡터공간 $V$의 부분공간 $U, W$가 있다고 할 때, $U \\cap W$도 $V$의 부분공간이다.$$Proof) \\\\forall k \\in \\R, \\forall v_1, v_2 \\in U \\cap W, \\ {} \\v_1, v_2 \\in U \\R
6.Null space

$m \\times n$ 행렬 $A$의 영공간은 $A$의 열벡터의 선형결합의 결과물을 $\\vec{0}$으로 만드는 선형결합의 계수들의 집합이다.$$Null(A) = {\\vec{x} | A\\vec{x} = \\vec{0}} \\subset \\R^n$$열공간이 $
7.Linear Independence

공집합이 아닌 벡터 집합 $S = {v_1, v_2, ..., v_r}$이 있을 때, $S$의 어떤 벡터도 다른 벡터들의 선형 결합으로 나타낼 수 없다면 $S$를 선형 독립이라고 한다.반면 $S$ 중 하나 이상의 벡터가 다른 벡터들의 선형 결합으로 나타낼 수 있을 때,
8.Span of vector space

Span 벡터공간 $V$의 공집합이 아닌 부분집합 $S$에 대해, $Span(S)$는 $S$의 벡터를 이용해 만들 수 있는 모든 선형 결합의 집합이다. Property on Span $Span(S)$는 $V$의 부분공간이다. $$ Proof) \\ Let \ S = \
9.생성집합과 선형종속의 관계성

무한체 $F$(ex. 실수/복소수) 위의 벡터 공간 $V$가 영공간이 아닐 때, $V$는 원소를 무한히 많이 가진다. 벡터들의 합과 스칼라 곱이 모두 $V$에 속하기 때문이다.만약 $V$를 생성하는 $V$의 작은 유한 부분집합 $S$가 존재한다면 $V$의 모든 원소를
10.벡터공간의 차원

벡터공간 $V$가 유한집합인 기저를 가질 때, $V$의 모든 기저는 유한집합이고 크기는 동일하다.기저가 유한집합인 벡터공간을 유한차원 벡터공간이라고 한다.$V$의 기저가 n개의 벡터로 이루어질 때 n을 $V$의 차원이라고 정의하고 $dim(V)$로 표기한다.유한차원 벡
11.기저 관련 정리, 부분공간의 차원

$V$가 유한차원 벡터공간이고 $dim(V) = n$이면 다음과 같은 성질을 지닌다.벡터공간 $V$의 기저는 $V$를 생성하며, 일차독립인 $V$의 부분집합이다.$V$는 유한집합인 기저를 포함한다. 이 때 $V$의 모든 기저는 유한집합이고 크기가 $n$으로 동일하다.$
12.라그랑주 보간법

무한체 $F$의 스칼라 $c_0, c_1, ..., c_n$이 주어졌다고 하자. 이 때 $c_i$ 각각에 대한 라그랑주 다항식을 다음과 같이 정의한다.$$fi(x) = \\frac{(x-c_0)...(x-c{i-1})(x-c{i+1})...(x-c_n)}{(c_i-c_
13.선형변환의 정의와 예시

벡터공간 $V, W$가 있다고 하자.함수 $T:V \\rightarrow W$가 모든 $x, y \\in V, c \\in F$에 대해$T(x+y) = T(x)+T(y)$$T(cx) = cT(x)$를 만족하면 함수 $T$를 $V$에서 $W$로 가는 선형변환이라고 한다.
14.Rank-Nullity Theorem

벡터공간 $V, W$에 대한 선형변환 $T : V \\rightarrow W$가 있다고 하자.1\. 영공간영공간은 $V$의 원소 중 함수값이 $W$의 영벡터인 것들의 집합이다.$$N(T) = {x \\in V | T(x) = 0_W}$$2\. 상공간상공간은 $T$의 치
15.단사,전사함수와 선형변환

벡터공간 $V, W$와 선형변환 $T : V \\rightarrow W$가 있을 때$T$는 전사함수 $\\equiv$ $N(T) = {0}$유한차원 벡터공간 $V,W$의 차원이 동일할 때, 선형변환 $T:V \\rightarrow W$에 대해 다음 명제들은 동치다.$T
16.선형변환의 행렬표현

유한차원 벡터공간의 기저에 특정한 순서가 부여되면, 이를 순서 기저라고 한다.예를 들어 $dim(V) = 3$인 벡터공간 $V$의 기저 $\\alpha = {v_1, v_2, v_3}, \\beta = {v_2, v_1, v_3}$이 있을 때, 둘은 기저의 벡터의 순서
17.선형변환의 합성과 행렬 곱

$F$-벡터공간 $V, W, Z$와 선형변환 $T: V \\rightarrow W, U: W \\rightarrow Z$가 있을 때, 두 선형변환의 합성 $UT : V \\rightarrow Z$는 선형변환이다.증명)$x, y \\in V$, $c \\in F$에 대해
18.행렬 곱과 선형변환의 관계성

$A$가 $m \\times n$, $B$와 $C$가 $n \\times p$ 행렬일 때, 다음이 성립한다. $\\$1\. $A(B+C) = AB+AC$2\. $a(AB) = (aA)B = A(aB)$3\. $I_mA = A = AI_n$증명)$(B + C){ij} =
19.선형변환의 가역성

벡터공간 $V, W$와 선형변환 $T:V \\rightarrow W$가 있다고 하자.$$TU = I_W, UT =I_V$$를 만족하는 함수 $U:W \\rightarrow V$를 $T$의 역함수라고 한다.역함수가 존재하는 $T$를 가역이라고 하며, $T^{-1}$로 표
20.동형사상
벡터공간 $V, W$에 대해 가역인 선형변환 $T: V \\rightarrow W$가 존재하면 $V$와 $W$는 동형(Isomorphic)이다. 이 때 $T$를 동형사상(Isomorphism)이라고 한다.예시)$T: F^2 \\rightarrow P_1(F), \\ T
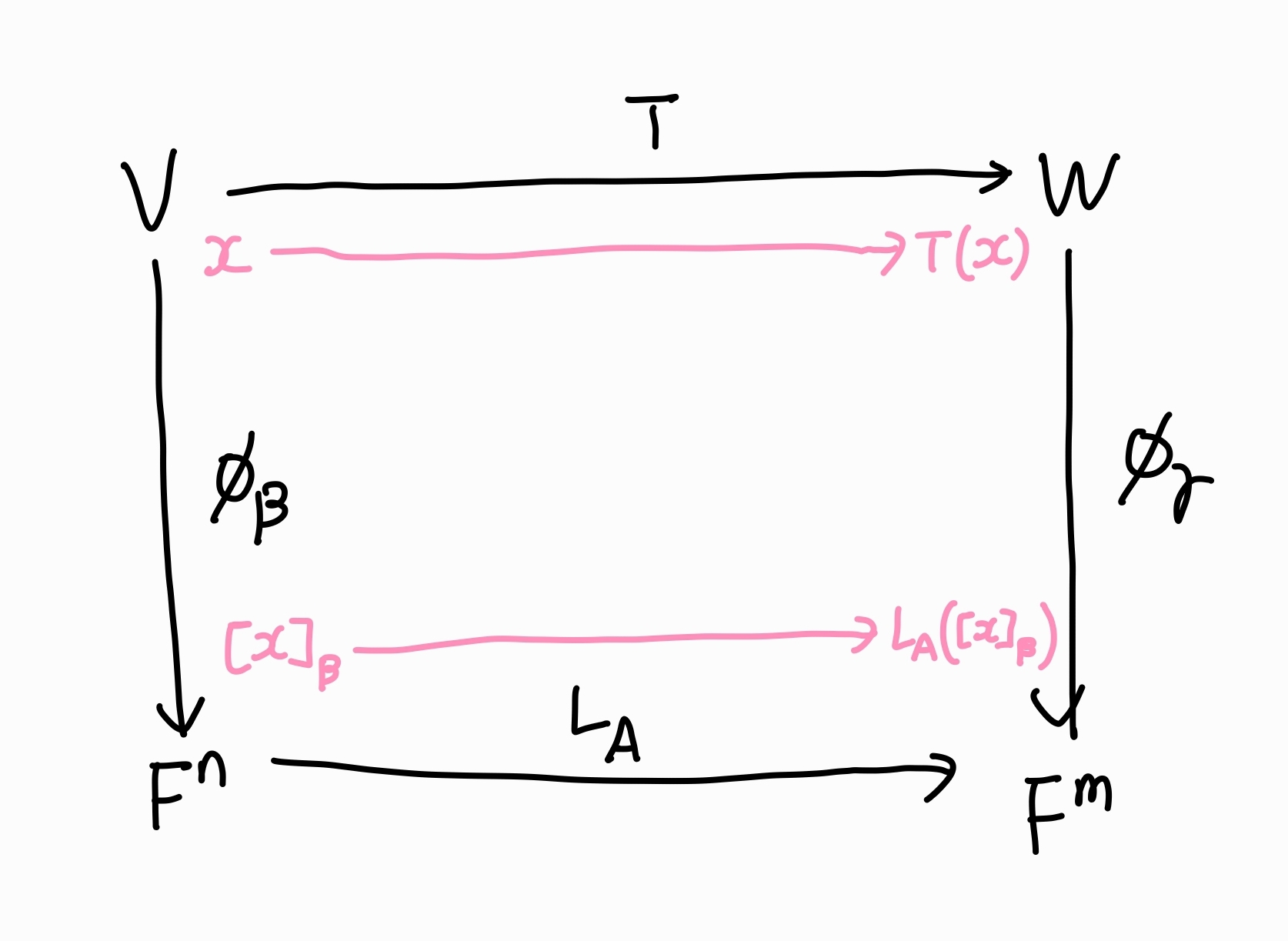
21.가역행렬의 조건

$V, W$가 각각 $n, m$ 차원이고 $\\beta, \\gamma$를 순서기저로 가지는 유한차원 벡터공간이라고 하자.$m \\times n$ 행렬 $A$가 가역행렬이라고 하자. $M{m \\times n}(F)$와 $ℒ(V, W)$은 동형사상이므로 $A=T\\be
22.좌표변환 행렬

기저는 벡터공간의 모든 원소를 유일한 방식으로 표현할 수 있게 해준다. 그러나 상황에 따라서 표준 순서 기저가 아닌 다른 기저를 이용할 때 데이터의 해석이 더 쉬운 경우도 있다. 따라서 동일한 벡터에 대한 한 기저의 표현을 다른 기저의 표현으로 옮길 수 있는 방법이 필
23.기본행렬연산과 기본행렬

$m \\times n$ 행렬 $A$에 대해 $A$의 행(열)연산을 다음과 같이 정의한다.$A$의 두 행(열)을 교환하는 것$A$의 한 행(열)에 영이 아닌 스칼라를 곱하는 것$A$의 한 행(열)에 다른 행(열)의 스칼라 배를 더하는 것위 세가지 행(열)연산을 통틀어
24.행렬의 랭크

행렬 $A \\in M\_{m \\times n}(F)$의 랭크는 선형변환 $L_A:F^n \\rightarrow F^m$의 랭크로 정의한다.$n \\times n$ 행렬 $A$에 대해서,$A$가 가역행렬 $\\Leftrightarrow$ $A$의 랭크가 $n$증명)$
25.가우스-조던 소거법

기본연산과 랭크 임의의 행렬에 기본행(열)연산을 적용한 행렬의 랭크는 원래 행렬의 랭크와 동일하다. 따라서 기본행(열)연산을 통해 랭크를 구하기 쉬운 꼴로 바꿀 수 있다면 원래 행렬의 랭크를 더 쉽게 구할 수 있다. 가우스-조던 소거법 > 랭크가 $r$인 $m \ti
26.역행렬의 계산

$n \\times n$ 가역행렬 $A$와 항등행렬 $I_n$이 있다고 하자. 이 때 $A$의 열과 $I_n$의 열을 가로로 붙여 $\\leftA | I_n \\right$의 첨가행렬을 만들 수 있다.이 때 $A^{-1}\\leftA | I_n \\right = \\l
27.연립일차방정식계

$$a{11}x_1 + ... + a{1n} = b1 \\a{21}x1 + ... + a{2n} = b2 \\\\vdots \\a{m1}x1 + ... + a{mn}x_n = b_m$$위와 같은 $n$개의 미지수와 $m$개의 방정식을 가지는 연립일차방정식계가 있을 때,
28.고유벡터와 고윳값

유한차원 벡터공간 $V$ 위의 선형연산자 $T$가 주어질 때,$T\_\\beta$가 대각행렬이 되도록 하는 $V$의 순서기저 $\\beta$가 존재하면 $T$는 대각화 가능이다.$n \\times n$ 행렬 $A$에 대해 $L_A$가 대각화 가능이면 $A$는 대각화 가