가설 검정, 기각역

가설 검정

확률 변수 $X$가 관심의 대상이고, $X$의 확률 함수가 $f(x; \theta)$로 주어진다고 하자. 이 때 $\theta$는 $\theta \in \Omega$를 만족하는 모수다.

먼저 가설은 모수의 값에 대한 주장을 의미한다. 예를 들어 $\theta$는 5다. $\theta$는 5 미만이다. 등이 가설의 예시가 될 수 있다.

가설 검정은 다음과 같은 형식을 가진다.
$H_0 : \theta \in w_0$ vs $H_1 : \theta \in w_1$

이 때 $w_0$과 $w_1$은 $\Omega$를 파티션 하는 두 집합이다. 즉 $w_0 \cap w_1 = \empty$, $w_0 \cup w_1 = \Omega$를 만족한다.

$H_0$은 귀무가설로, 보통 기존의 통념/연구 결과와 모수 값이 동일함을 의미한다.
$H_1$은 대립가설로, 기존의 연구 결과와 차이 또는 변화가 있다는 주장이다.

두 가설 모두 모수에 대한 주장일 뿐 그 자체로는 가설 입증이 불가능하다.
따라서 $X$의 랜덤 표본 $X_1, X_2, ..., X_n$을 근거로 가설을 입증한다.

가설 검정은 보수적으로 대립 가설을 평가한다. 기본적으로 귀무 가설을 참이라고 생각하되, 귀무 가설이 참이라고 할 때 도저히 나오기 힘든 표본/검정통계량이 나온다면 귀무 가설을 기각한다는 것이다.

기각역

기각역은 표본을 바탕으로 귀무 가설을 기각할지 여부를 정하는 기준의 역할을 한다.

$D$를 표본 $(X_1, X_2, ..., X_n)$의 서포트라고 할 때, $D$의 어떤 부분집합을 기각역이라고 한다. 아래서 살펴볼 오류의 관리나 검정의 목적에 따라 필요한 기각역의 형태가 달라진다.

기각역을 $C$라고 할 때, $(X_1, X_2, ..., X_n) \in C$이면 귀무 가설을 기각한다. 반대로 $(X_1, X_2, ..., X_n) \in C^C$이면 귀무 가설을 기각하지 않는다.

1종 오류와 2종 오류

표본은 모집단의 일부이기 때문에 표본을 이용해 내리는 결론은 실제 모집단과 일치하지 않을 수 있다. 따라서 가설 검정의 결과 자체도 오류의 가능성을 포함하고 있다.

실제 모집단에서의 사실과 가설 검정의 결과의 관계를 표로 만들면 다음과 같다.

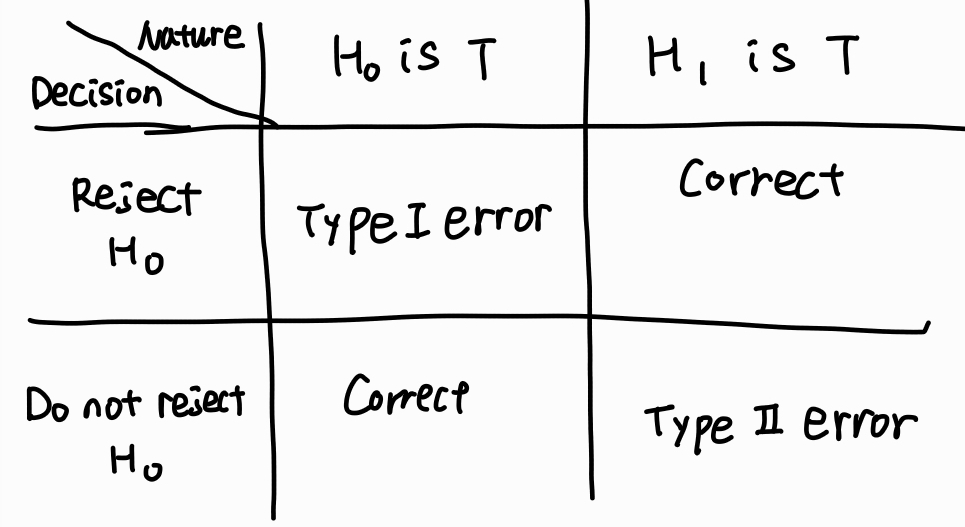
실제로는 귀무가설이 참이지만 표본이 우연히 극단적으로 나와서 귀무가설을 기각하는 오류를 1종 오류라고 한다.

반대로 대립가설이 참이지만 표본이 충분히 극단적으로 나오지 않아서 귀무가설을 기각하지 못하는 오류를 2종 오류라고 한다.

보통 1종 오류를 2종 오류보다 심각하게 여긴다. 1종 오류를 제대로 관리하지 못하면 기존의 연구 결과가 검정 한번으로 뒤집히는 등 학문의 안정성을 보장할 수 없기 때문이다.

1종 오류와 2종 오류의 상충 관계

1종 오류와 2종 오류는 한 쪽이 늘어나면 한 쪽이 줄어드는 관계에 있다. 따라서 두 오류를 동시에 줄이는 것을 불가능하다.

1종 오류를 줄이려면 그만큼 귀무 가설을 기각하기 힘들게 해야 하는데, 이는 곧 실제로는 대립 가설이 참임에도 불구하고 귀무 가설을 기각하지 못하는 2종 오류의 확률을 높이기 때문이다.

반대로 2종 오류를 줄이려면 귀무 가설을 기각하기 쉽게 해야 하는데, 이러면 1종 오류의 확률이 늘어난다.

오류를 고려한 기각역의 설정

따라서 기각역을 설정할 때는 더 중요한 1종 오류를 먼저 관리하고, 2종 오류의 확률을 낮추는 방향을 진행한다. 더 구체적으로는 다음의 과정을 거친다.

1종 오류 발생의 최대 확률을 통제

귀무 가설은 $\theta \in w_0$이기 때문에 $w_0$ 안의 원소라면 무엇이든 모수의 후보가 될 수 있다.

따라서 1종 오류를 통제한다는 것은 모든 $\theta \in w_0$에 대해서 1종 오류가 발생하는 확률의 상한선을 정한다는 것이다. 이를 $\alpha$라고 한다.

이렇게 $\alpha$를 지정하면 어떤 $\theta \in w_0$이 주어지든 1종 오류의 확률은 $\alpha$ 이하가 된다.

2종 오류 발생 확률을 최소화

$\alpha$가 지정 되면 이를 만족하는 기각역의 후보들을 구할 수 있다. 그 중 2종 오류가 발생 확률이 가장 작은 기각역이 제일 효율적인 기각역이 된다.

따라서 기각역의 후보들 중 $\theta \in w_1$에 대해 $P_\theta[(X_1, X_2, ..., X_n) \in C\lvert H_1 \ is \ true]$를 최대화 하는 기각역이 가장 효율적인 기각역이다.

$\gamma_C(\theta) = P_\theta[(X_1, X_2, ..., X_n) \in C \lvert H_1 \ is \ true]; \ \theta \in w_1$를 기각역 $C$의 검정력 함수(power function)이라고 한다.

만약 $C_1$, $C_2$가 있을 때, $\forall \ \theta \in w_1, \ \gamma_{C_1}(\theta) \ge \gamma_{C_2}(\theta)$를 만족하면 $C_1$이 $C_2$보다 좋은 기각역이라고 할 수 있다.