양측 검정, p-value

STATS·2023년 7월 11일

수리통계학

목록 보기

27/40

양측 검정

단측 검정은 $H_0 : \mu = \mu_0$ vs $H_1 : \mu > \mu_0$ 형식의 대립 가설에서 주장하는 모수의 방향성이 뚜렷하게 나타나는 검정을 의미했다.

그러나 대립 가설이 모수의 방향성을 나타내는 것이 아니라, 단순히 귀무 가설의 부정을 증명하고자 하는 경우 양측 검정을 실시한다.

$H_0 : \mu = \mu_0$ vs $H_1 : \mu \ne \mu_0$

따라서 기각역도 한 쪽이 아닌 분포의 양 쪽에 있어야 한다. 일반적인 예시로 기각역 $C$ 를
$C = \{\bar{X} \le X \ or \ \bar{X} \ge k \}$ 로 정의하자.

이 때 기각역의 크기 $\alpha$ 는 $\alpha = P_{H_0} (\bar{X} \le h \ or \ \bar{X} \ge k)= P_{H_0}(\bar{X} \le h)+ P_{H_0}(\bar{X} \ge k)$ 이다.

양측 검정 예시

확률 변수 $X$ 가 정규분포 $N(\mu, \sigma^2)$ 을 따른다고 하자. $\mu$ 는 모수이고, $\sigma^2$ 은 알려져 있는 상수다.

이 경우 $\bar{X} \sim N(\mu, \sigma^2/n)$ 이므로 표준 정규 분포를 이용해 검정을 진행할 수 있다.

$H_0 : \mu = \mu_0$ vs $H_1 : \mu \ne \mu_0$ 로 가설이 주어졌을 때, 검정통계량으로 $\bar{X}$ 를 표준화한 $\frac{\bar{X} - \mu_0}{\sigma / \sqrt{n}}$ 을 이용할 수 있다.

\alpha / 2 = P_{H_0}(\frac{\bar{X} - \mu_0}{\sigma / \sqrt{n}} \le -z_{\alpha / 2}), \ \alpha / 2 = P_{H_0}(\frac{\bar{X} - \mu_0}{\sigma / \sqrt{n}} \ge z_{\alpha / 2}) \\ { }\\ C = \{\frac{\bar{X} - \mu_0}{\sigma / \sqrt{n}} ; \lvert \frac{\bar{X} - \mu_0}{\sigma / \sqrt{n}}\lvert \ge \alpha/2\}

따라서 표본 평균의 실현값 $\bar{x}$ 가 나왔을 때, $\frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}} \in C$ 이면 귀무 가설을 기각한다. 반대로 $\frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}} \notin C$ 이면 귀무 가설을 기각하지 않는다.

실제 $\mu$ 의 위치에 따른 기각의 확률을 알아보기 위해 검정력 함수를 다음과 같이 구한다.

\gamma(\mu) = P_{\mu}(\bar{X} \le \mu_0 -z_{\alpha / 2}\frac{\sigma}{\sqrt{n}} \ or \ \bar{X} \ge \mu_0 + z_{\alpha / 2}\frac{\sigma}{\sqrt{n}}) \\ {} \\ = P_{\mu}(\bar{X} \le \mu_0 -z_{\alpha / 2}\frac{\sigma}{\sqrt{n}}) + P_{\mu}( \bar{X} \ge \mu_0 + z_{\alpha / 2}\frac{\sigma}{\sqrt{n}}) \\ {} \\ = P_{\mu}(\frac{\bar{X} - \mu}{\sigma / \sqrt{n}} \le -z_{\alpha / 2} + \frac{\sqrt{n} (\mu_0 - \mu)}{\sigma}) +P_{\mu}(\frac{\bar{X} - \mu}{\sigma / \sqrt{n}} \ge z_{\alpha / 2} + \frac{\sqrt{n}(\mu_0 - \mu)}{\sigma}) \\ {} \\ = Φ(-z_{\alpha / 2}+ \frac{\sqrt{n}(\mu_0 - \mu)}{\sigma}) + 1 - Φ(z_{\alpha / 2}+\frac{\sqrt{n}(\mu_0 - \mu)}{\sigma}) \\ {} \\ \Rightarrow r'(\mu) = \frac{\sqrt{n}}{\sigma}[φ(\frac{\sqrt{n}(\mu_0 - \mu)}{\sigma} + z_{\alpha / 2})-φ(\frac{\sqrt{n}(\mu_0 - \mu)}{\sigma}-z_{\alpha / 2})]

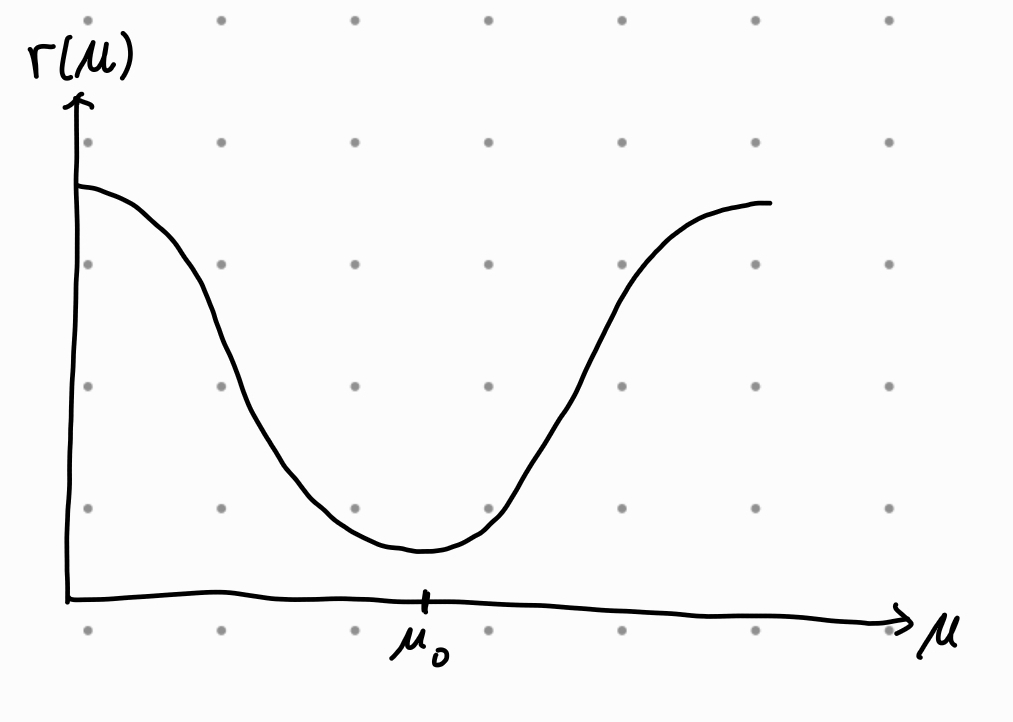
$r(\mu)$ 를 그려보면 $\mu = \mu_0$ 에서 극소점을 가지는 개형을 보이는데, 귀무가설에서 주장하는 $\mu_0$ 에서 $\mu$ 값이 멀어질수록 귀무 가설을 기각할 확률이 높아지는 것을 알 수 있다. 단측 검정과는 달리 기각역이 양쪽에 존재하기 때문에 검정력 함수가 단조 증가 함수가 아니다.

양측 검정과 신뢰 구간의 관계성

H_0 \text{을 기각하지 않음} \equiv -z_{\alpha / 2} < \frac{\bar{X} - \mu_0}{\sigma/\sqrt{n}} < z_{\alpha / 2}\\ {} \\ \equiv \mu_0 - z_{\alpha / 2}\frac{\sigma}{\sqrt{n}} < \bar{X} < \mu_0 + z_{\alpha / 2}\frac{\sigma}{\sqrt{n}} \\ {} \\ \equiv \bar{X} - z_{\alpha / 2}\frac{\sigma}{\sqrt{n}} < \mu < \bar{X}+ z_{\alpha/2}\frac{\sigma}{\sqrt{n}}

따라서 추출한 표본 평균으로 만든 $100(1-\alpha)$ % 신뢰 구간이 $\mu$ 를 포함한다면 $H_0$ 을 기각하지 않는다. 반대로 $100(1-\alpha)$ % 신뢰 구간이 $\mu$ 를 포함하지 않는다면 $H_0$ 를 기각한다.

p-value

p-value는 검정통계량이 귀무가설 하에서 어느 정도의 극단성(나오기 힘든 정도)을 가지는지 알려주는 확률 값이다. p-value는 다음과 같이 정의한다.

p-value = P_{H_0}(T \ge t)

$T$ 는 검정통계량의 확률 변수를 의미하며, $t$ 는 표본을 토대로 계산한 검정통계량의 실현값을 의미한다.

p-value가 크다는 것은 귀무가설 하에서 $T=t$ 인 사건이 발생할 확률이 상대적으로 높다는 것이고, 따라서 귀무 가설을 기각하기에 충분한 근거가 되지 못한다.

반대로 p-value가 작다는 것은 귀무 가설 하에서 $T=t$ 인 사건이 발생할 확률이 작다는 것을 의미한다. 따라서 귀무 가설이 원 분포가 아니라는 의심을 충분한 근거를 가지고 할 수 있기 때문에, 이런 경우 귀무 가설을 기각한다.

STATS

이전 포스트

가설 검정, 기각역

다음 포스트