가우스-조던 소거법

기본연산과 랭크

임의의 행렬에 기본행(열)연산을 적용한 행렬의 랭크는 원래 행렬의 랭크와 동일하다. 따라서 기본행(열)연산을 통해 랭크를 구하기 쉬운 꼴로 바꿀 수 있다면 원래 행렬의 랭크를 더 쉽게 구할 수 있다.

가우스-조던 소거법

랭크가 $r$인 $m \times n$ 행렬 $A$에 대해서, $r \le m, r \le n$이 성립한다.
또한 기본행(열)연산을 유한 번 사용해서 $A$를 다음과 같은 꼴로 바꿀 수 있다.

$D = \begin{pmatrix} I_r & O_1 \\ O_2 & O_3 \end{pmatrix}$

이 때 $i \le r$이면 $D_{ii} = 1$, 그렇지 않으면 $D_{ij} = 0$이고 $O_1, O_2, O_3$은 영행렬이다.

증명)

1. $A = O$면 $r=0$이다. 따라서 $D = A$이고, 증명이 끝난다.
2. $A \neq O$일 때 $r = rank(A)$이면 $r > 0$이다.
   $A$의 행의 개수 $m$에 대한 수학적 귀납법을 이용하자.

$m=1$일 때, 두 열을 교환하는 열연산과 한 열에 스칼라를 곱하는 열연산을 각각 최대 한번씩 사용해서 첫 열의 원소를 1로 만들 수 있다. 그 후 1열의 원소에 스칼라를 곱해 다른 열에 더하는 연산을 최대 $n-1$번 해서 $d = (1 \ 0 \ ... \ 0)$ 꼴로 만들 수 있다.
이 때 $D$의 일차독립인 열은 하나이기 때문에 $Rank(A) = Rank(D) = 1$이다.

어떤 자연수 $m > 1$에 대해 최대 $m-1$개의 행을 가지는 임의의 행렬에서 이 정리가 성립한다고 가정하자. 그렇가면 $m$개의 행을 가지는 임의의 행렬에 대해서도 이 정리가 성립함을 보이면 증명은 끝난다.

$A$가 $m \times n$ 행렬이라고 가정하자. $n=1$인 경우, 위에서와 동일하지만 이번에는 행연산을 이용해서 $D = \begin{pmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{pmatrix}$ 꼴로 만들 수 있다.
이 경우에도 원래 행렬인 $A$의 일차독립인 열의 개수 = $D$의 일차독립인 열의 개수 = 1이므로 $Rank(A) = Rank(D) = 1$이다.

$n > 1$일 때, $A\neq O$이므로 어떤 $i, j$에 대해 $A_{ij} \neq 0$이다. 따라서 행을 교환하는 행연산과 열을 교환하는 열연산을 각각 최대 한번씩 사용해서 1행 1열의 값이 0이 아니도록 만들 수 있다. 그 후 1행을 1행 1열의 값으로 나누는 행연산을 진행하면, 1행 1열의 값은 1이 된다.

이제 1행 1열을 이용해 행연산을 최대 $m-1$번, 열연산을 최대 $n-1$번 해서 1행과 1열 각각에서 1행 1열은 제외한 모든 성분을 0으로 만들 수 있다. 그 결과는 다음 행렬과 같다.

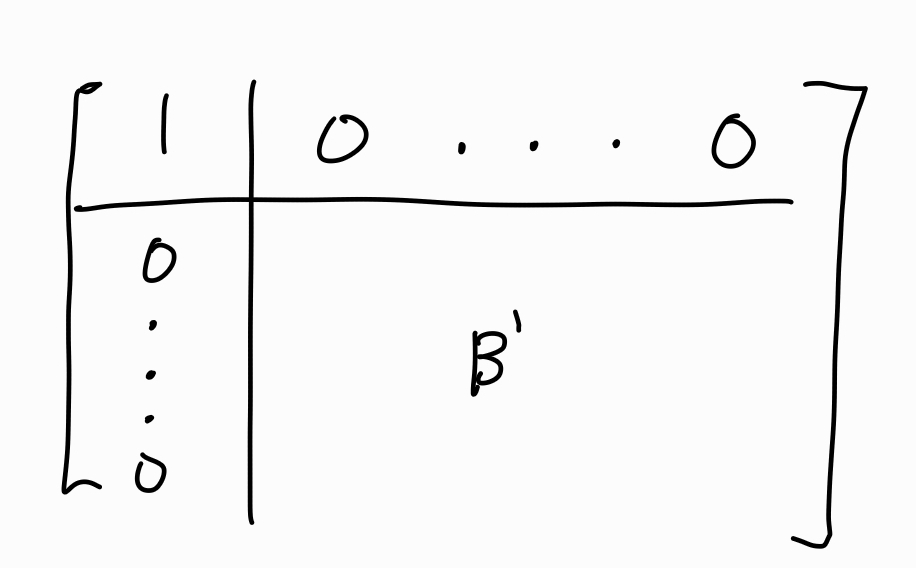
이 때 $B'$의 랭크는 $r-1$이고, 귀납법의 가정에 의해 $r-1 \le m-1$이고 $r-1 \le n-1$이므로 $r \le m$, $r \le n$이다.

귀납적으로 $B'$에도 같은 작업을 반복해서 첫 $r$개의 대각성분이 1이 될 때까지 반복하자. 그 결과로 다음과 같은 행렬 $D$를 완성할 수 있다.

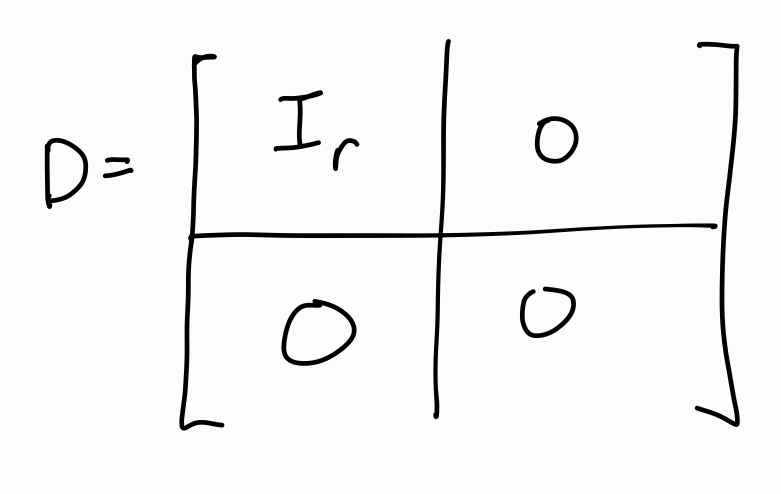
따라서 $A$에 유한번의 행연산과 열연산을 이용해서 $D$를 완성할 수 있고, $D$는 첫 $r$개의 대각성분이 1이고 그외 성분은 모두 0인 행렬이다. 따라서 증명이 완료된다.

기본행렬과 가우스 조던 소거법

랭크가 $r$인 $m \times n$ 행렬 $A$에 대해 다음을 만족하는 $m \times m$ 가역행렬 $B$와 $n \times n$ 가역행렬 $C$가 존재한다.

$D = \left[ \begin{array}{c|c} I_r & O_1 \\ \hline O_2 & O_3 \end{array} \right] =BAC$

증명)
앞의 정리에 따르면 $A$에 유한번의 행연산과 열연산을 적용시켜 $D$를 구할 수 있다. 그런데 각각의 행연산과 열연산은 하나의 기본행렬에 대응된다. 따라서 각 행연산의 기본행렬을 $E_i$, 열연산의 기본행렬을 $G_j$에 대응하면 다음을 만족한다.

그리고 모든 기본행렬은 가역이므로 기본행렬의 곱들도 가역이다. 따라서 $B$와 $C$는 가역행렬이다.

$m \times n$ 행렬 $A$에 대해 다음이 성립한다.

1. $rank(A^t) = rank(A)$
2. 임의의 행렬의 랭크는 일차독립인 행의 최대 개수와 같다.
3. 임의의 행렬의 행과 열은 차원이 같은 부분공간을 생성한다. 차원은 행렬의 랭크와 같다.

증명)
1.
위의 증명에 따르면 어떤 기본행렬들의 곱 $B$, $C$가 존재해서 $D = BAC$를 만족한다. 이 때 $rank(A) = rank(D)$이고, 첫 $rank(D)$개의 대각성분은 1이고 나머지 성분은 0이다.
랭크는 일차독립인 열벡터의 최대 개수인데, $D$의 랭크는 대각성분 중 1의 개수와 동일하다.

이제 $D^t$의 경우를 살펴보자. $D^t$의 경우도 마찬가지로 대각성분의 위치는 변하지 않고, 나머지 성분은 모두 0이므로 $D^t$의 랭크는 $D$와 동일하다. 따라서 $rank(A) = rank(D) = rank(D^t)$를 얻는다.

그리고 $rank(D^t) = rank(C^tA^tB^t)$에서 $C^t$와 $B^t$가 가역행렬이므로 $rank(D^t) = rank(A^t)$이다. 따라서 $rank(A) = rank(A^t)$다.

2.
$rank(A) = rank(A^t)$이므로 $A$의 일차 독립인 최대 열의 개수와 $A^t$의 일차 독립인 최대 열의 개수는 동일하다.

그런데 $A^t$의 열벡터의 배치는 $A$의 행벡터의 배치와 동일하다. 따라서 $A^t$의 일차 독립인 열벡터들의 최대 개수는 $A$에서 일차 독립인 행벡터들의 최대 개수와 동일하다.

따라서 $Rank(A^t) = Rank(A) = \text{A에서 일차 독립인 행벡터의 최대 개수}$이다.

3.

행벡터들의 집합을 $R$이라고 하자. 일차종속인 벡터들을 $R$에서 제거하면 집합 $R' \subset R$을 만들 수 있다. 이 때 $span(R) = span(R')$이다. 그리고 $R'$은 모두 일차독립인 벡터들이므로 $R'$은 $span(R)$의 기저가 된다.

마찬가지로 열벡터들에 대해서도 일반성을 잃지 않고 위 과정을 적용하면 열벡터들의 집합 $C$에 대해 일차종속인 벡터들을 모두 제거한 $C' \subset C$가 $span(C)$의 기저가 됨을 알 수 있다.

그리고 2.에 의해 행렬 $A$에서 일차독립인 행벡터와 열벡터의 최대 개수는 행렬의 랭크로 동일하다. 따라서 $R'$의 벡터 개수와 $C'$의 벡터 개수는 동일하고, $span(R)$과 $span(C)$의 차원도 행렬의 랭크로 동일하게 된다.

행렬 곱의 랭크와 행렬의 랭크

유한차원 벡터공간 $V, W, Z$ 사이에 정의된 선형변환 $T: V \rightarrow W, U: W \rightarrow Z$와 행렬곱 $AB$를 정의하는 두 행렬 $A, B$에 대해 다음이 성립한다.

$1. rank(UT) \le rank(U)$
$2. rank(UT) \le rank(T)$
$3. rank(AB) \le rank(A)$
$4. rank(AB) \le rank(B)$

증명)
1.

2.
벡터공간 $T(V)$의 기저를 $\beta = \{v_1, ..., v_k\}$라고 하자. $U(\beta) = \{U(v_1), ..., U(v_k)\}$는 $U(T(V))$의 생성집합이다. 따라서 $U(T(V))$의 기저의 크기는 k이하가 된다. 만약 $s \ge k$가 $U(T(V))$의 기저의 크기가 된다면 k개의 벡터로는 $U(T(V))$를 생성할 수 없기 때문이다.

따라서 $dim(U(T(V)) \le k$이고, $dim(U(T(V)) \le dim(T(V)) \Rightarrow Rank(UT) \le Rank(T)$가 성립한다.

3.4.
3.과 4.는 위에서 증명한 1.과 2.의 구체적인 응용이다.

라는 성질을 이용하고, 1.과 2.를 이용하면 3.과 4.를 바로 증명할 수 있다.