동형사상

동형사상

벡터공간 $V, W$에 대해 가역인 선형변환 $T: V \rightarrow W$가 존재하면 $V$와 $W$는 동형(Isomorphic)이다. 이 때 $T$를 동형사상(Isomorphism)이라고 한다.

예시)
$T: F^2 \rightarrow P_1(F), \ T(a_1, a_2) = a_1+a_2x$일 때, T는 선형변환이고 $T^{-1}(b+cx) = (b, c)$를 만족한다. 따라서 $V$와 $W$는 동형이고 $T$는 동형사상이다.

동형사상과 벡터공간의 차원

같은 체 위에서 정의된 유한차원 벡터공간 $V, W$에 대해

$V$와 $W$가 동형 $\equiv$ $dim(W) = dim(V)$

증명)
$(\Rightarrow)$ $V$와 $W$가 동형이면 가역인 선형변환 $T:V \rightarrow W$가 존재한다.
$T$가 가역이고, $V$가 유한차원이므로 $dim(V) = dim(W)$이다.

$(\Leftarrow)$ $V$의 순서기저 $\beta = \{v_1, ..., v_n\}$, $W$의 순서기저 $\gamma = \{w_1, ..., w_n\}$이 있다고 하자.

$T(v_i) = w_i$인 선형변환 $T:V \rightarrow W$가 존재한다. $R(T) = span(T(\beta))=span(\gamma) = W$에서 $R(T) = W$이므로 $T$는 전사이고, $dim(W) = dim(V)$이기 때문에 $T$는 단사다.

따라서 $T$는 가역이기 때문에 $V$와 $W$는 동형이고 $T$는 동형사상이다.

선형변환과 행렬의 동일성

$F$-벡터공간 $V, W$가 $dim(V) = n$, $dim(W) = m$이고, $v$와 $w$의 순서기저가 각각 $\beta, \gamma$일 때,

$\Phi_\beta^\gamma : ℒ(V, W) \rightarrow M_{m \times n}, \Phi_\beta^\gamma (T) = [T]_\beta^\gamma$은 동형사상이다.

증명)
$\Phi$가 선형변환이고 가역임을 증명하면 $ℒ(V, W)$, $M_{m \times n}$은 동형이므로 증명이 완료된다.

먼저 선형변환임을 증명하자.
임의의 $T, U \in ℒ(V, W), \ c \in F$에 대해 $cT \in ℒ(V, W)$이기 때문에 $[cT+U]_\beta^\gamma = [cT]_\beta^\gamma + [U]_\beta^\gamma = c[T]_\beta^\gamma + [U]_\beta^\gamma$ 이므로 $\Phi_\beta^\gamma$는 선형변환이다.

다음으로 $\Phi_\beta^\gamma$가 가역임을 증명하자.
$\beta = \{v_1, ..., v_n\}, \ \gamma = \{w_1, ..., w_m\}$일 때,
임의의 $m \times n$ 행렬 $A$에 대해 $T(v_j) = \sum_{i=1}^m A_{ij}w_i$를 만족하는 선형변환 $T: V \rightarrow W$는 항상 존재하며, 유일하다.
따라서 $\Phi_\beta^\gamma$는 우선 전사이다. 그리고 모든 행렬에 선형변환이 유일하게 대응되기 때문에 $\Phi_\beta^\gamma$는 단사다.

결론적으로 $\Phi_\beta^\gamma$는 가역이므로 $ℒ(V, W)$와 $M_{m \times n}$는 동형이고, $\Phi_\beta^\gamma$는 동형사상이다.

$ℒ(V, W)$의 차원

위의 결과에서 $ℒ(V, W)$과 $M_{m \times n}$는 동형임을 얻었다.

$M_{m \times n}$이 유한차원 벡터공간이고 $M_{m \times n}$와 동형이므로 $ℒ(V, W)$도 유한차원이고, 이로부터 $dim(ℒ(V, W)) = dim(M_{m \times n}) = mn$을 얻는다.

벡터공간의 표준표현

체 $F$위의 $n$차원 벡터공간 $V$의 순서기저를 $\beta$라고 하자.

$\beta$에 대한 $V$의 표준표현은 선형변환 $\phi_\beta : V \rightarrow F^n$이며, $x \in V$에 대해 $\phi_\beta (x) = [x]_\beta$로 정의한다.

일반적인 선형변환과 좌측 곱 변환의 관계성

임의의 유한차원 벡터공간 $V$와 순서기저 $\beta$에 대해 $\phi_\beta$는 동형사상이다.

증명)
$\phi_\beta$는 선형변환이기 때문에 $\phi_\beta$가 가역임을 증명하면 된다.

$V$의 순서기저 $\beta = \{v_1, ..., v_n\}$이고, $F^n$의 표준순서기저 $\{e_1, ..., e_n\}$이 있다고 하자.
이 때 $T(v_i) = e_i$를 만족하는 선형변환 $T: V \rightarrow F^n$은 항상 존재하고 유일하다.

임의의 $(c_1, ..., c_n) \in F^n$에 대해 $x = c_1v_1 + ...c_nv_n \in V$가 존재해서 $T(x) = c_1T(v_1) + ... + c_nT(v_n) = (c_1, ..., c_n)$을 만족한다. 따라서 $T = \phi_\beta$는 전사함수다.

그리고 임의의 $c_1, c_2 \in F$에 대해 $c_1 \neq c_2$이면 대응하는 $x_1 \neq x_2$이므로 $\phi_\beta$는 단사함수다.

따라서 $\phi_\beta$는 가역이고, $V$와 $F^n$은 동형이므로 $\phi_\beta$는 동형사상이다.

선형변환과 좌측 곱 변환

차원이 각각 $n, m$인 벡터공간 $V, W$와 선형변환 $T:V \rightarrow W$에 대해서,
$\beta, \gamma$가 각각 $V$와 $W$의 순서기저라고 하자.

이 때 $A = [T]_\beta^\gamma$라고 하면, 선형변환 $T$와 선형변환 $L_A : F^n \rightarrow F^m$의 관계성을 파악할 수 있다.

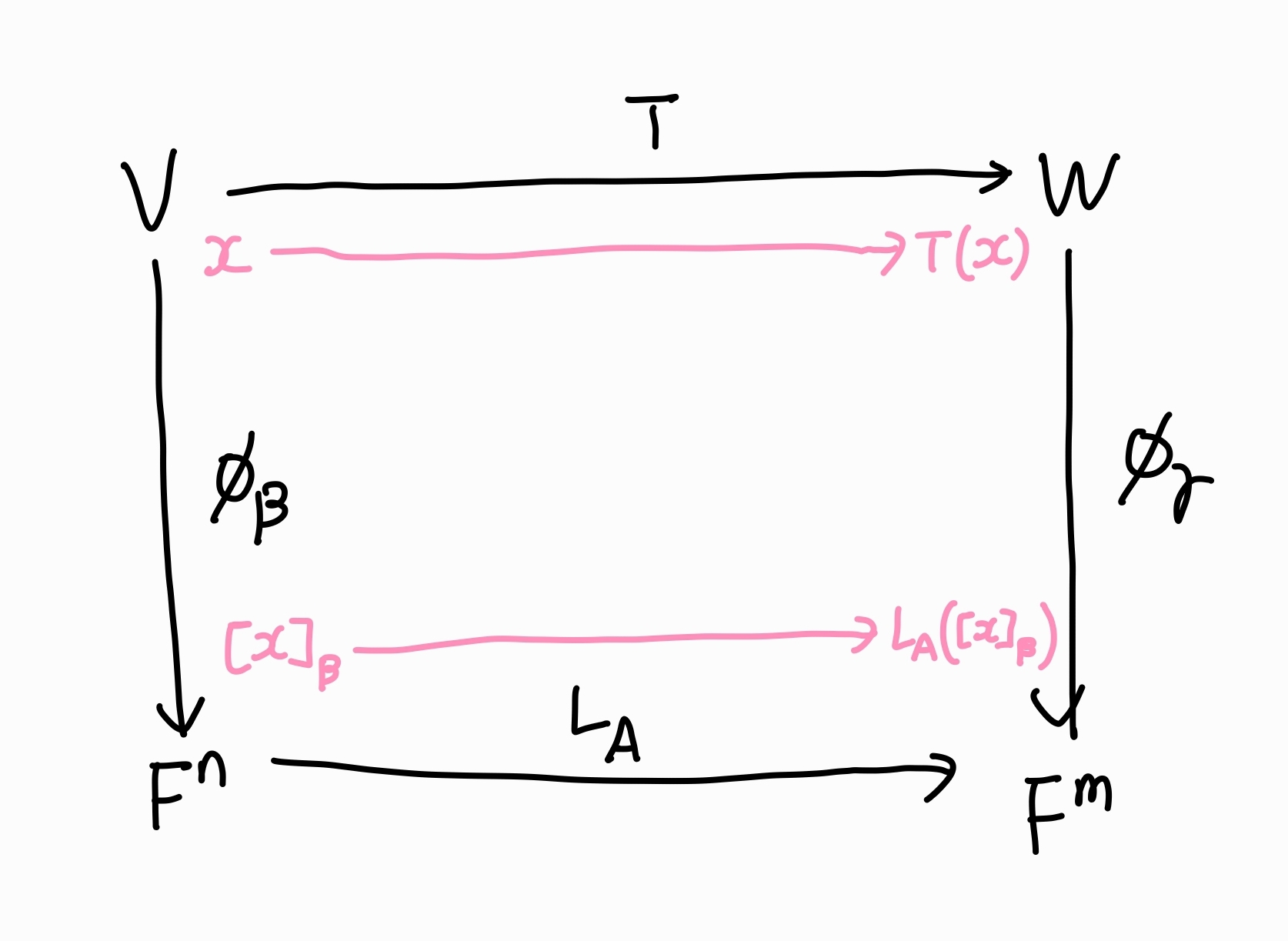
위의 그림에 따르면 $V$에서 $F^m$으로 가는 방법은 두가지가 있다.

첫번째는 합성된 선형변환 $L_A\phi_\beta$를 이용하는 것이다. 먼저 $x$를 $[x]_\beta$로 변환한 후 $L_A$를 이용해 $[x]_\beta$를 $A[x]_\beta = [T]_\beta^\gamma [x]_\beta = [T(x)]_\gamma$로 나타낸다.

두번째로는 합성된 선형변환 $\phi_\gamma T$를 이용할 수 있다. 먼저 $x$를 $T(x)$로 변환한 후, $\phi_\gamma$를 이용해 $T(x)$를 $[T(x)]_\gamma$로 변환한다.

따라서 두방법 중 어느 것을 선택하든 동일한 결론에 도달할 수 있다. 이는 $V$와 $F^n$, $W$와 $F^m$이 동형이기 때문에 가능하다.