비편향추정량

MSE

추정량도 확률변수이기 때문에 확률시행의 결과에 따라 값이 달라진다. 바람직한 추정량의 경우 추정량의 값이 모수와 거의 비슷해야 모수 추정의 의미가 있다.
따라서 모수와 추정량의 거리를 재는 측도를 설정한 후, 그 측도를 바탕으로 추정량의 성능을 평가한다.

보통 모수와 추정량의 거리의 측도로 MSE를 사용한다.

따라서 추정량과 모수의 평균적인 거리가 크다면 MSE는 커지고, 반대로 추정량과 모수의 평균적인 차이가 작다면 MSE는 작아진다.

그런데 동일한 추정량의 MSE도 $\theta$에 따라 그 값이 달라진다. 즉 모수가 $\theta_0$일 때는 MSE가 충분히 작았던 추정량이 모수가 $\theta_1$인 경우에는 평균적인 거리차가 너무 커지는 불균형이 발생할 수 있다.

비편향추정량

따라서 모든 모수 $\theta$에 대한 균형있는 추정을 보장하기 위해 (MSE가 모든 모수의 경우에 대해 너무 큰 차이가 나지 않기 위해), 추정량의 비편향성이라는 좋은 추정량의 조건을 이용한다.

비편향추정량

$T(X)$가 모수 $\theta$의 추정량이라고 할 때, $E[T(X)] - \theta$를 $T(X)$의 편향(bias)이라고 한다.
만약 $E[T(X)] = \theta$, 즉 편향이 0이라면 $T(X)$를 $\theta$의 비편향추정량(unbiased estimator)이라고 한다.

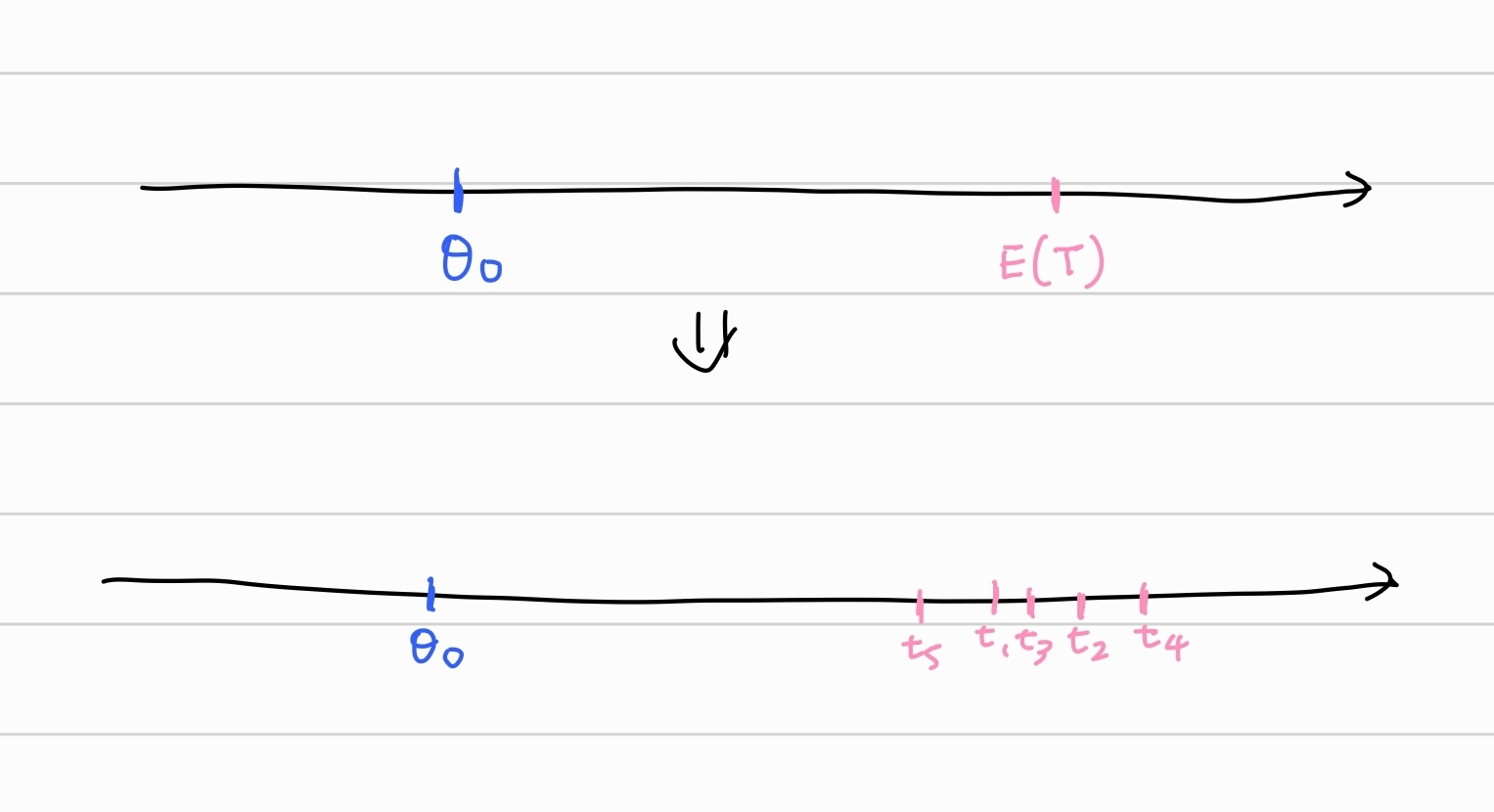
만약 추정량의 편향이 존재하는 경우는 추정량이 추출되는 무게중심(평균)이 원래 모수에서 떨어져 있다는 것이다. 따라서 추정량의 실현도 모수를 중심으로 추출되지 않는다.

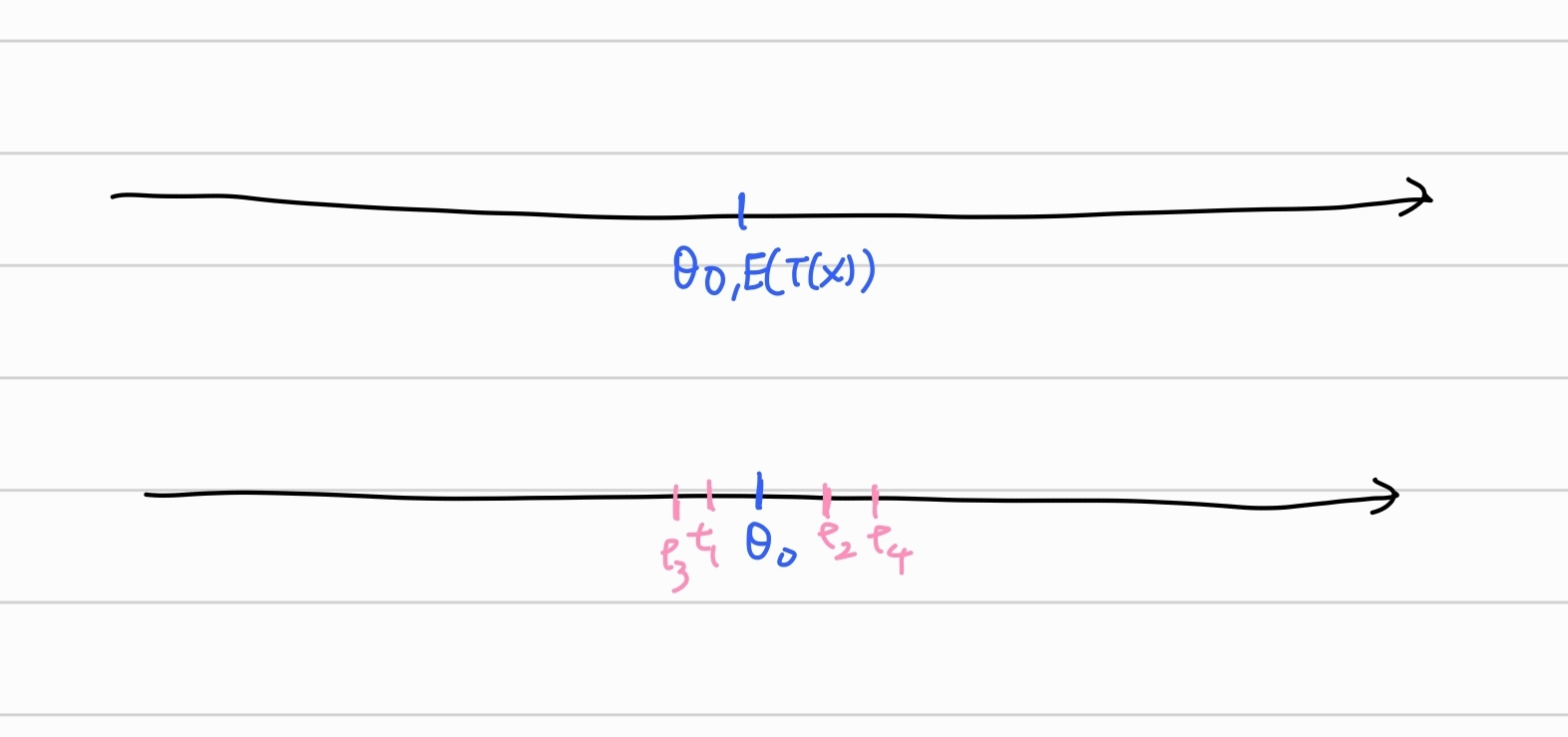
반면 추정량의 편향이 존재하지 않는다면 추정량의 실현은 원래의 모수를 기준으로 추출된다. 추정량 추출의 무게중심이 원래의 모수가 되므로 모수의 추정량의 실현들의 평균적인 거리가 최소가 된다.

분산과 편향

MSE는 앞서 설명한 편향, 그리고 추정량의 분산이라는 두가지 요소로 분리할 수 있다.

따라서 MSE를 최소화 하기 위해서는 추정량이 비편향성을 가지면서 동시에 그 분산이 작아야 한다.