abstract
Online RL은 sample inefficiency와 instability 라는 문제를 갖고 있다
Offline RL 은 distributional shift라는 문제를 갖고 있다
- 선행연구 중 one-step importance weighting(full trajectory importance weighting)을 통해 distribution shift를 피한 케이스가 있다
→ 적은 분산과 함께 작은 gradient estimate 을 유도할 수 있다
-
이 연구에서는 off-policy actor critic을 사용해 distribution shift를 해결한다
-
이번 연구를 통해 softmax policy parameterization 은 지나치게 긍정적인 예측을 유도해 Out Of Distribution action을 유발할 수 있다
Introduction
기존 supervised learning 방식의 한계점
- long term satisfaction을 만족시키기 힘들다
- strong feedback loop 가 myoptic behavior(근시안적인 행동) 를 강화시켜 문제를 야기한다
bandit 과 RL의 장점
- 수학적인 근거를 제공
- feedback loop 이 만든 sub-optimal system을 극복할 수 있는 exploration과 off-policy learning을 사용할 수 있다
Contributions
1) recommender system 을 위한 off-policy actor critic
2) critic network 구성 방법에 대한 충고와 critic network learning에 중요한 critical components : ex) TD learning setup, feature 의 중요성, target network, 아키텍처 선정
3) critic 이 예측한 Q 값과 MC return 을 비교해 target과 behavior policy 를 비교하는 분석 툴 제작
4) offline 실험 환경 제작
Offline learning target 과 behavior policy 간의 괴리를 해결해오던 방식
- behavior 와 target policy 간 비슷하도록 하는 constrain 걸기
- off-policy data 에서 관찰되지 않은 action에 패널티를 가해 behavior policy를 추측할 필요를 없앰
- action value function 만 배우고 max 를 취하는 방식으로 policy를 이로부터 결정
→ 이 논문에서는 actor-critic 방식 도입
1) stochastic policy for introducing exploration ?
2) implicit 하게 비관적인 해석을 하기 때문에 over estimation 문제를 해결
Background
Recommender system에서 MDP는 다음과 같이 정의된다

state 를 나타낼 때 user의 과거 interaction 을 기반으로 만든 user state를 취함을 알 수 있다
아래와 같은 목적함수를 최대화하는 방향으로 훈련이 진행된다
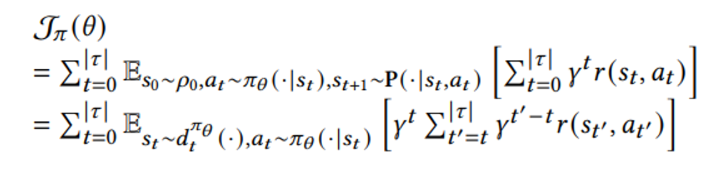
두 번째 줄 수식에서 d_t 는 policy pi_theta에서 state visitation frequency를 의미한다
policy paramter theta에 대해 미분하면 아래와 같은 결과를 얻는다
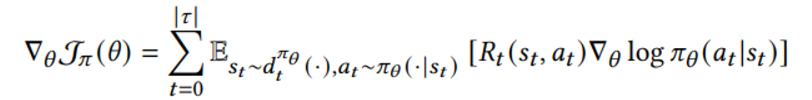
이 때 timestep t R 은 다음과 같이 정의된다
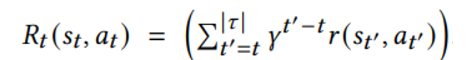
(현재 step에서 horizon 까지 discount 하고 더하기 때문에 estimated return을 의미)
(위의 식과 비교하면 두 번째 줄의 gamma^t 항을 생략함)
Offline RL 환경에서는 훈련 데이터를 생성하는 behavior policy의 distribution 이 다르므로 전통적인 importance sampling 방식을 고려하면
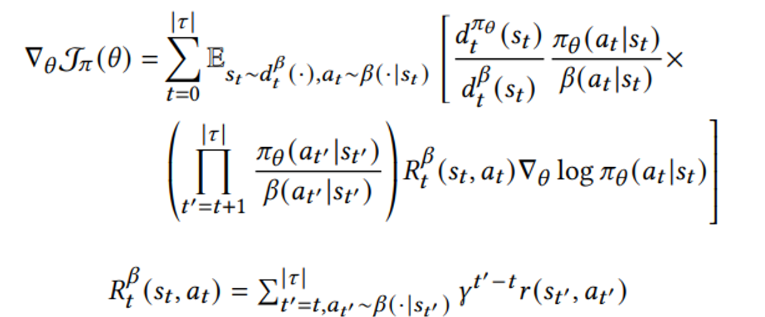
하지만 위와 같이 전체 trajectory 에 대한 importance sampling은 너무 큰 variance를 유발
First-order approximation을 통해 보다 적은 variance, 하지만 biased 된 갑을 얻는다 (R^beta로 표현된 behavior policy를 통해 얻은 trajectory에서 MC 로 뽑은 값은 target policy 값을 대표할 수 없다)
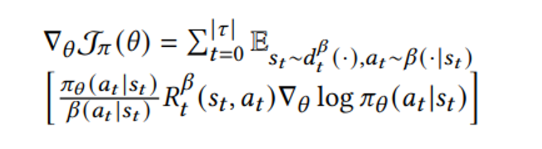
Method
이 논문은 actor-critic 방식을 차용한다
policy 를 근사하는 parameter theta 뿐만 아니라 critic도 NN로 근사하게 되는데 이를 behavior policy 로부터 MC 로 얻은 R^beta를 대치할 수 있다
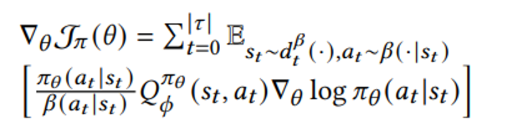
수식상으로는 R → Q 로 대치된다
이러한 방식은 위위 수식에서 R_t가 유도하던 cummulative return 으로 인한 bias를 줄일 수 있게 해준다
수식상에서 원래 cummulative reward 항 R_t 에 붙던 importance weight 항은 사라졌지만 아직 first-order weight가 남아있음을 알 수 있는데
이는 a~beta (action이 behavior policy에서 sample 되기 때문에) 를 보정하기 위해 남아있는 것이다
Q-value 함수는 아래와 같은 TD- error 를 최소화하는 방향으로 훈련된다
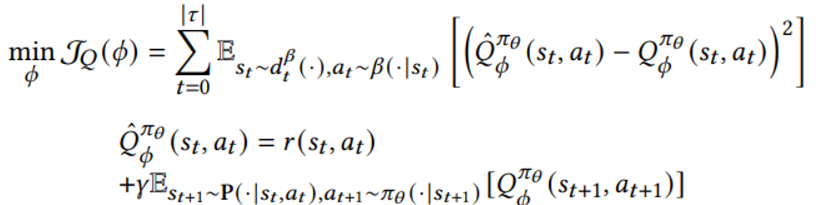
Outlier를 처리하기 위해? Huber loss (delta = 10) 를 적용했다
- 아직 state transition을 모르는데 Q estimation 값을 어떻게 구할 것인가..?
1) behavior policy를 통한 importance sampling
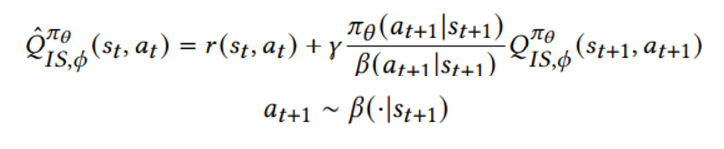
장점
- behavior policy 에 support 가 있는 상태에서 next state에 대해 Q estimate 하는 것이 더 정확하다
- 현재와 next state에 대해 모두 user feedback 이 존재하는 상황이기 때문에 critic이 이를 추가로 받아 개선할 여지가 존재한다
단점
- learned policy가 behavior policy가 커버하지 못하는 action space에서 action을 취할 경우 value 가 under estimate 된다
- learned policy가 behavior policy 와 distribution 에서 차이를 보일 경우 importance sampling은 분산을 증가시킨다
2) samplig from learned policy
conventional 한 방법은 learned policy에서 직접 action을 추출하는 것이다
장점
- behavior policy가 커버하진 못한 action space에 대한 영역을 걱정할 필요가 없다
- 여러번의 next timestep action과 Q 근사값의 평균을 통해 분산을 감소시킬 수 있다
단점
- behavior policy에 존재하지 않는 action의 경우 Q value가 정확하지 않게 측정될 수 있다 (action embedding 이 정확하게 학습되지 않을 수 있음)
- 어떤 state에서 택하지 않았던 action을 선택하는 경우 user feedback을 알 수 없으므로 feedback signal을 통해 critic network를 학습시킬 수 없다
→ 이 단점은 궁금했던 부분이긴 한데 만약 feedback 이 integer 형태로 주어지는 경우 예전에 읽은 논문이 zero reward 주는 방식으로 생각해볼 수 있지 않을까?
Sampled Softmax
Recommder system에서 action space가 너무 크기 때문에 전체 집합의 일부분인 집합(C)를 sample하고 다음과 같은 비례관계에 따라 next timestep action을 선정한다
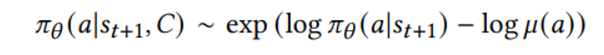
Target network
RL community에서 안정적인 gradient update를 위해 사용하는 target network 개념을 그대로 사용한다 (update parameter : 0.1)
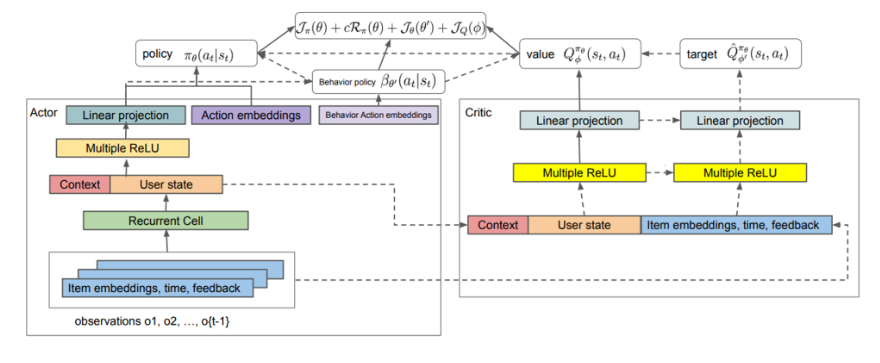
Overall architecture