신박Ai님의 [Deep Learning 101] Cross Entropy 크로스엔트로피 손실함수를 알아보자 강의를 정리하였습니다.
정보 (Information, 놀람, suprisal)
확률
: 가능한 모든 상황에서 어떤 이벤트가 발생하는 빈도수
99개의 파란 종이와 1개의 빨간 종이, 총 100개의 종이로 제비뽑기를 한다고 가정하면,
파란 종이를 뽑을 확률은 99%이고, 빨간 종이를 뽑을 확률은 1%이다.
이때, 사람들은 파란 종이를 뽑으면 시큰둥하겠지만, 빨간 종이를 뽑는다면 매우 놀랄 것이다. 즉, 확률이 높으면 그 사건이 발생해도 별로 놀라지 않고, 확률이 낮으면 그 사건이 발생했을 때 많이 놀라게 된다.
즉, 확률과 놀람은 무언가 서로 반비례의 개념이다.
놀람을 수학적으로 표현하자면, 확률을 로 할 경우 놀람은 확률의 역수, 로 표현할 수 있다.
실제 정보이론에서 정의하는 놀람의 공식은 이다.
정보를 효율적으로 전달하기 위한 방법으로 log를 사용하였다.
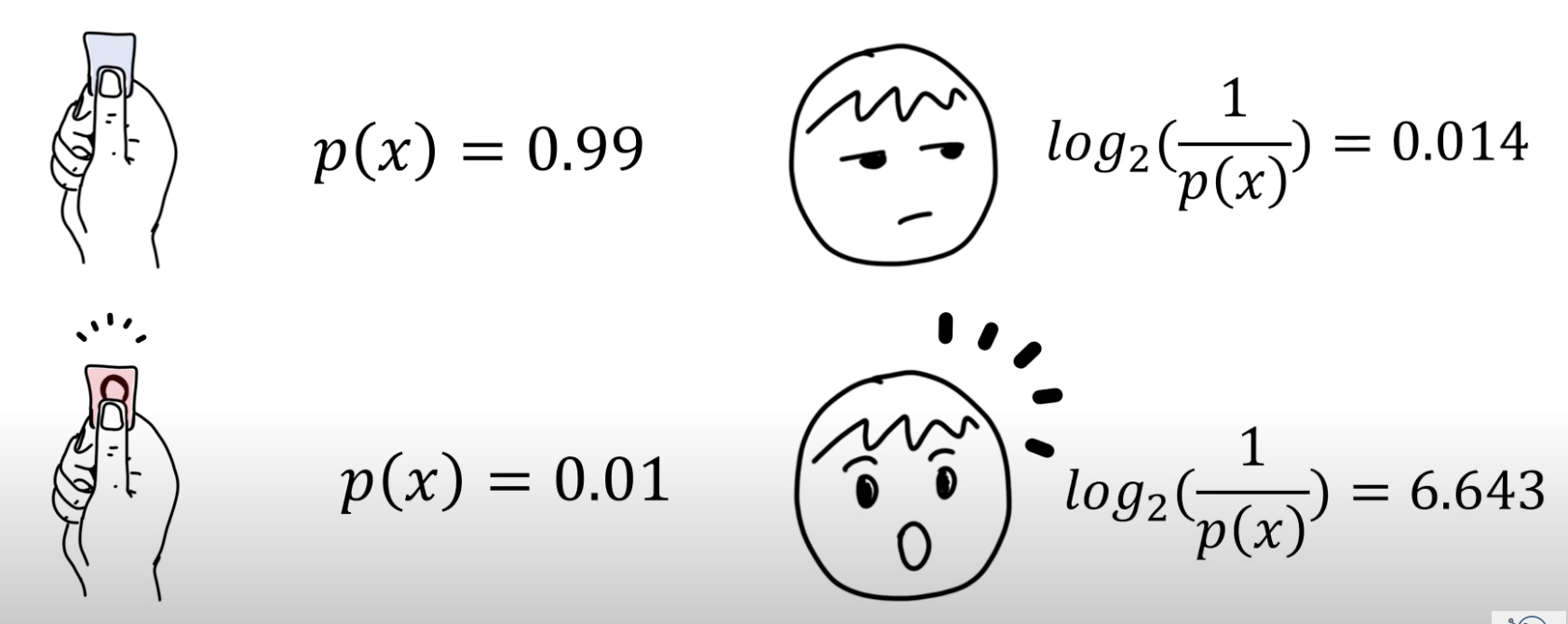
정보이론에서 정보란 일종의 의외성, 놀람을 객관적인 수치로 표현한 것을 말한다.
일종의 놀람도라고 생각하면 된다. 보통 놀람이라는 것은 주관적이고 심리적인 현상이기 때문에, 정보이론에서는 보다 객관적인 지표의 의미가 있는 정보라는 단어를 사용한다.
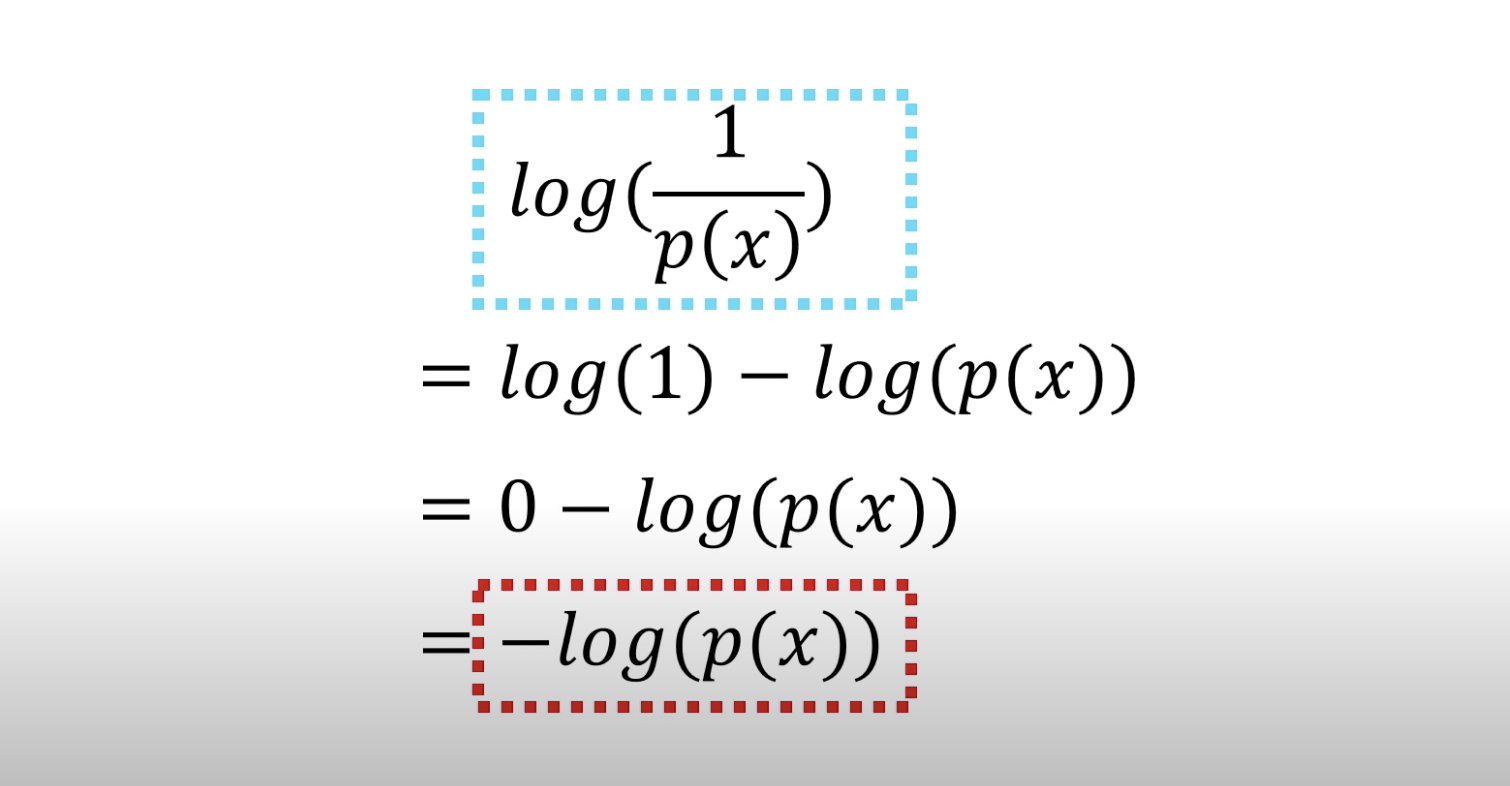
하지만 여기서는 그 이름이 정보가 되었든, 놀람이 되었든, 그 의미가 확률에 반비례하는 것을 기억하면 된다!
기댓값 (Expectation value)
: 어떤 값에 확률을 곱한 값
신박 FC와 AI FC가 축구 경기를 한다고 가정하면,
기본적으로 축구 경기의 승패는 각 선수의 기량에 따라 좌우가 된다.
각 선수들의 기량의 평균을 구해보았을 때, 객관적인 전력면에서는 신박FC가 높다고 볼 수 있다.
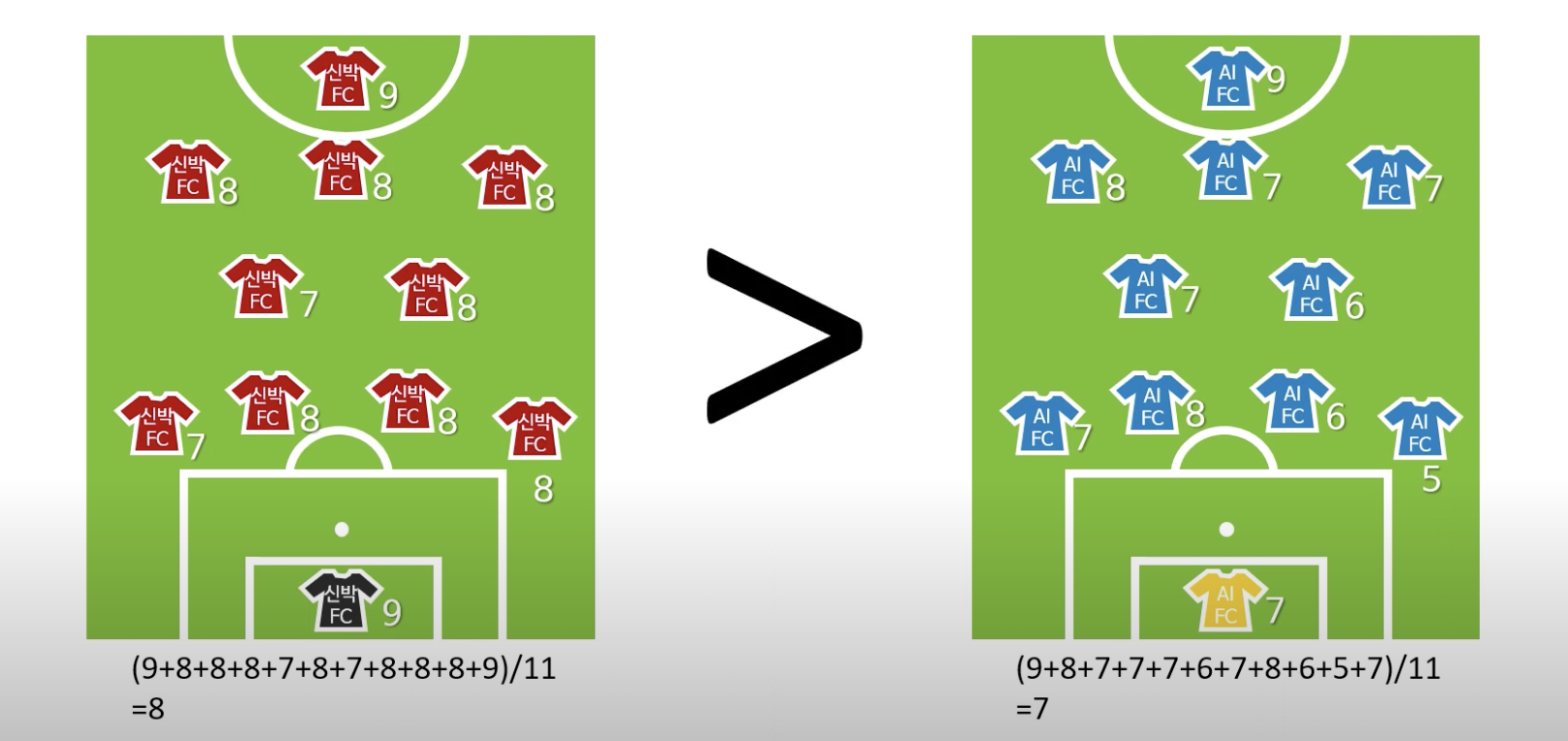
그러나, 객관적 전력이 높다고 신박FC가 무조건 이기는 것은 아니다.
컨디션에 따라 제 기량을 100% 발휘하지 못하는 경우도 있기 때문에 각각의 기량에 제 기량을 발휘할 확률을 곱해보면 AI FC의 값이 더 큰 것을 확인할 수 있다.
이렇게 각각의 기량에 제 기량을 발휘할 확률을 곱한 것은 각 팀의 그날 예상되는 기대 전력이라고 볼 수 있다.
한 선수의 오늘 예상 실력 = 객관적인 선수의 기량 x 그 기량이 오늘 발휘될 확률
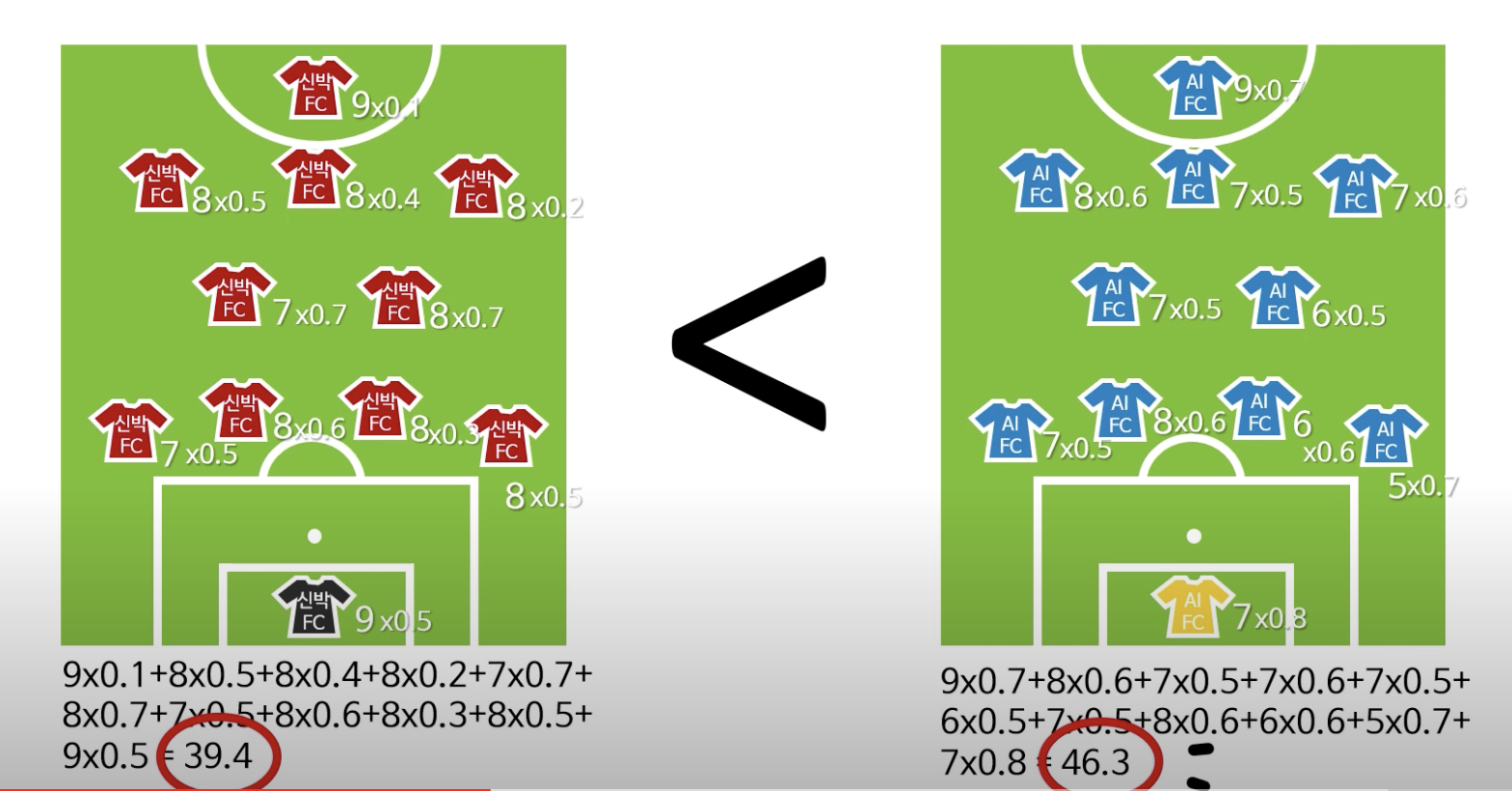
이렇게 어떤 값에 확률을 곱한 값을 기댓값이라고 부른다.
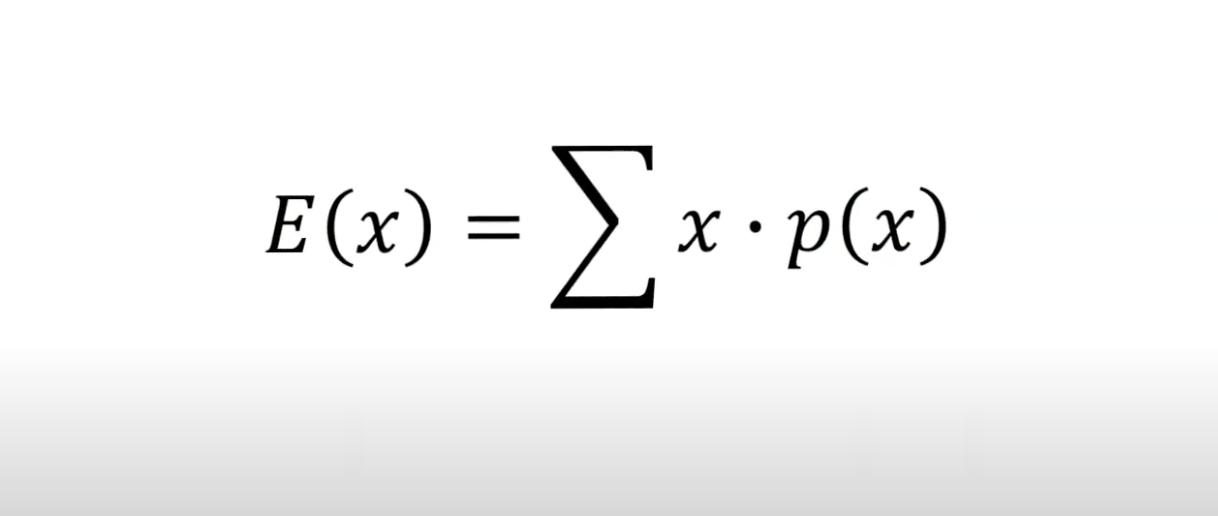
엔트로피 (Entropy)
: 놀람의 예상 값 (즉, 기대놀람도)
위에서 살펴본 기댓값 공식에서 (객관적 전력, 수치)대신 놀람도를 넣으면 엔트로피 공식이 된다.
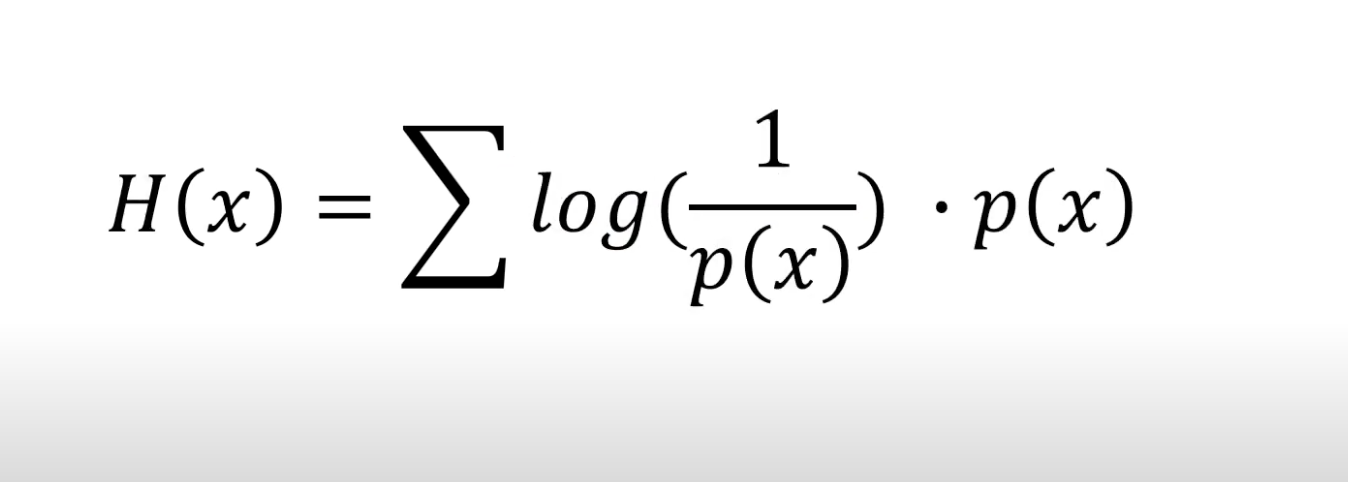
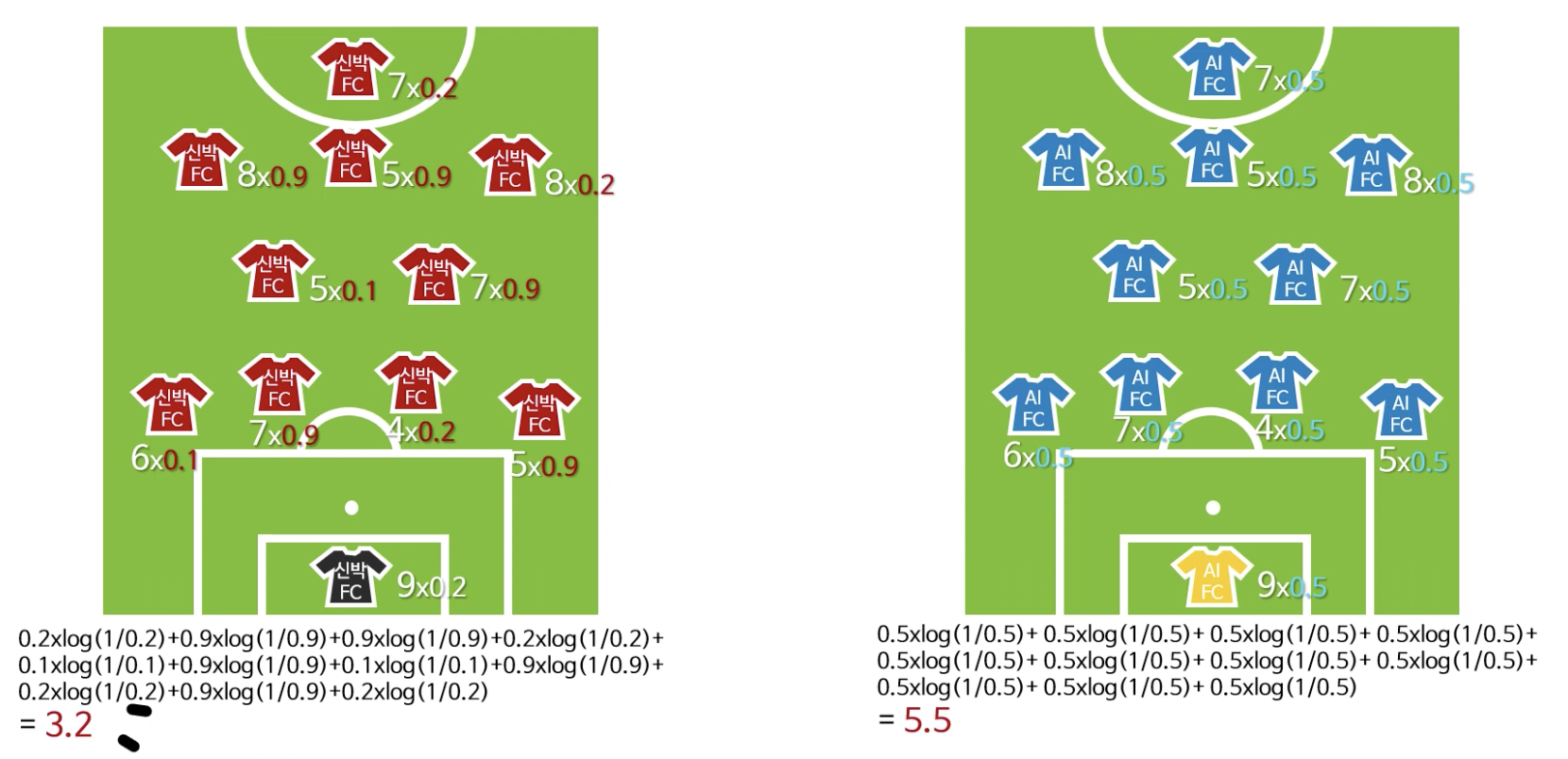
위에서 예시를 들었던 축구 경기로 다시 가정을 해보면,
다음과 같이 예상되는 기대 전력의 값이 동일할 경우에는 어떤 팀의 승리 확률이 높은지 예상하기 쉽지 않다.
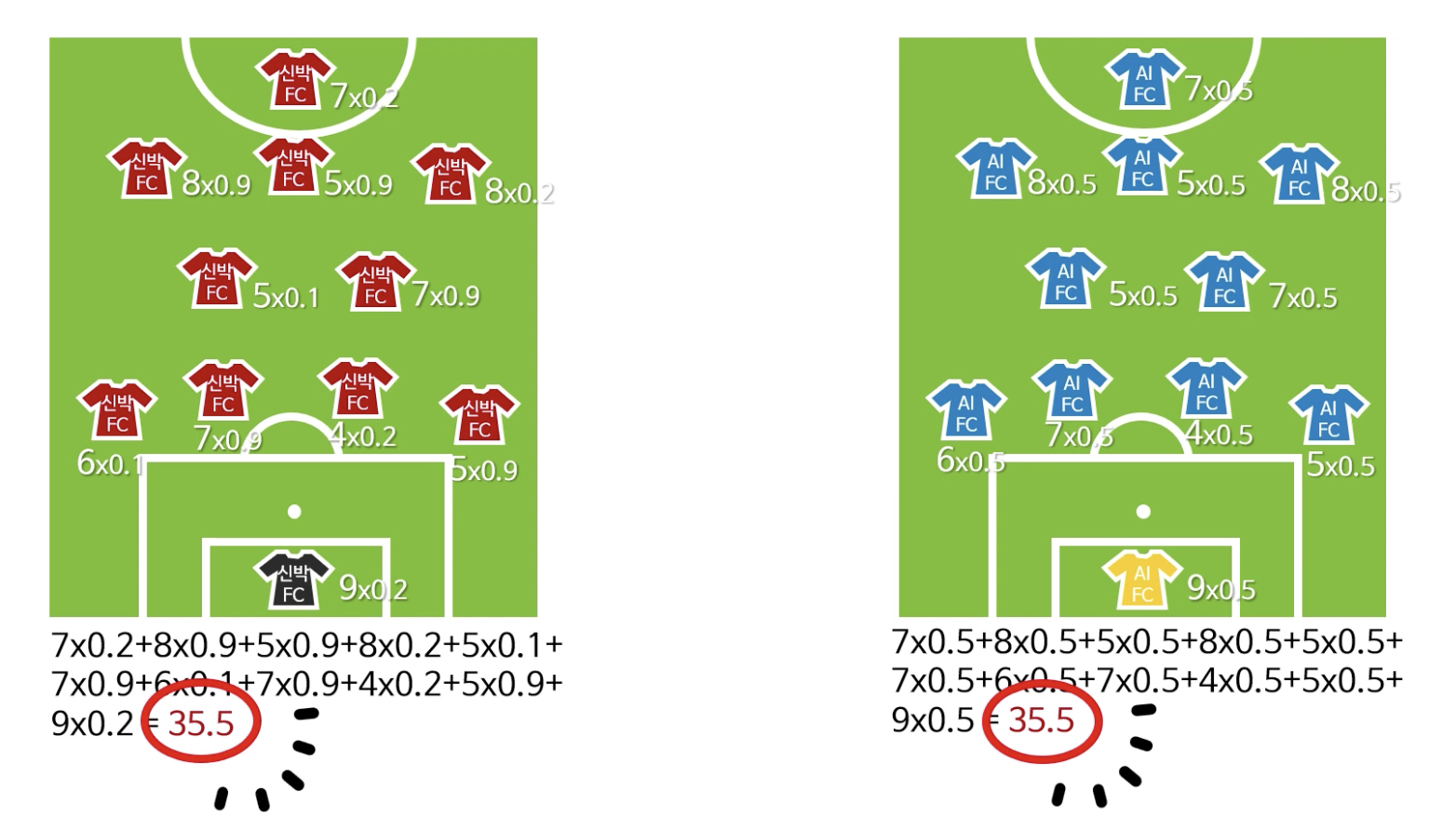
이런 경우, 엔트로피를 이용해볼 수 있다.
예를 들어, 확률이 0.9 또는 0.1인 선수들은 안정적으로 잘하거나 못하는 선수라는 것을 예측해볼 수 있다. 결국 예측 가능성이 더 높다는 뜻이다.
이렇듯 예측 가능성을 계산할 때 엔트로피가 이용된다.
엔트로피는 어떤 사건들을 예상치 못한 경우가 많아질 때 높아지는 경향이 있다.
크로스 엔트로피 (cross entropy)
크로스 엔트로피의 공식은 엔트로피 공식에서 하나만 바꾸면 된다.
즉, 의 확률에 의 놀람도를 곱하는 것이다.
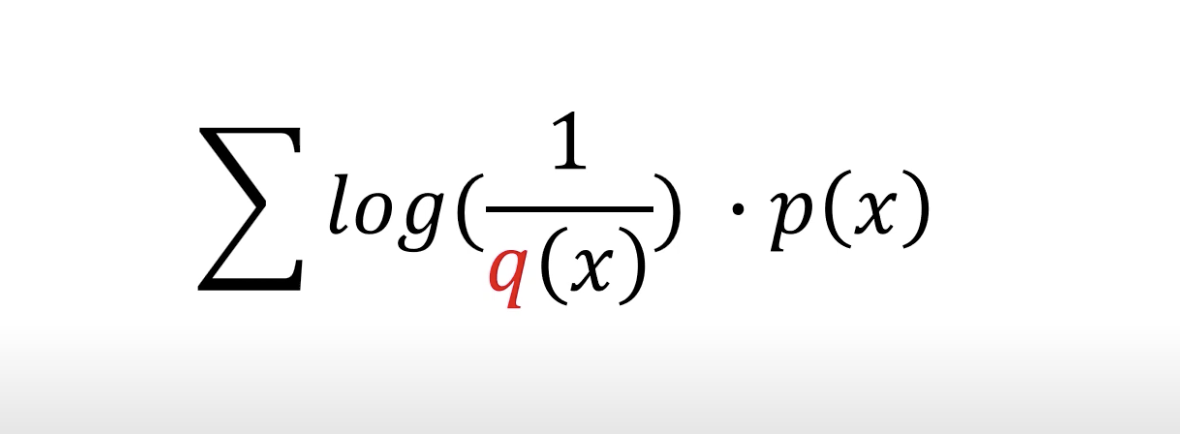
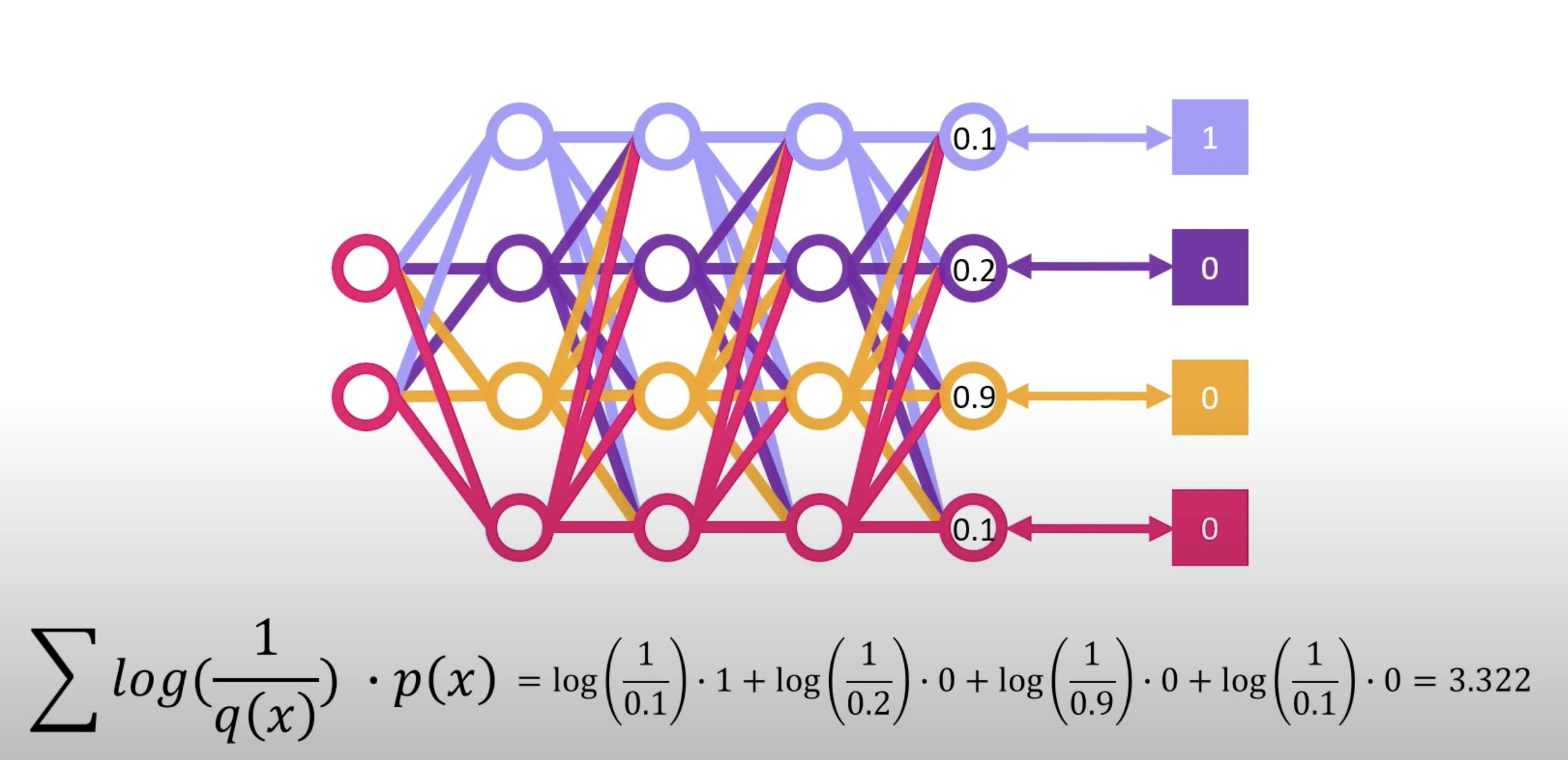
만약 주어진 정답이 있고, 신경망을 통해 도출되는 출력 값이 이와 같다면, 신경망은 불편함을 느낀다.
크로스 엔트로피 공식을 통해 다음과 같이 loss를 계산할 수 있고, 이 loss가 작아지는 방향으로 가중치를 업데이트하게 된다.
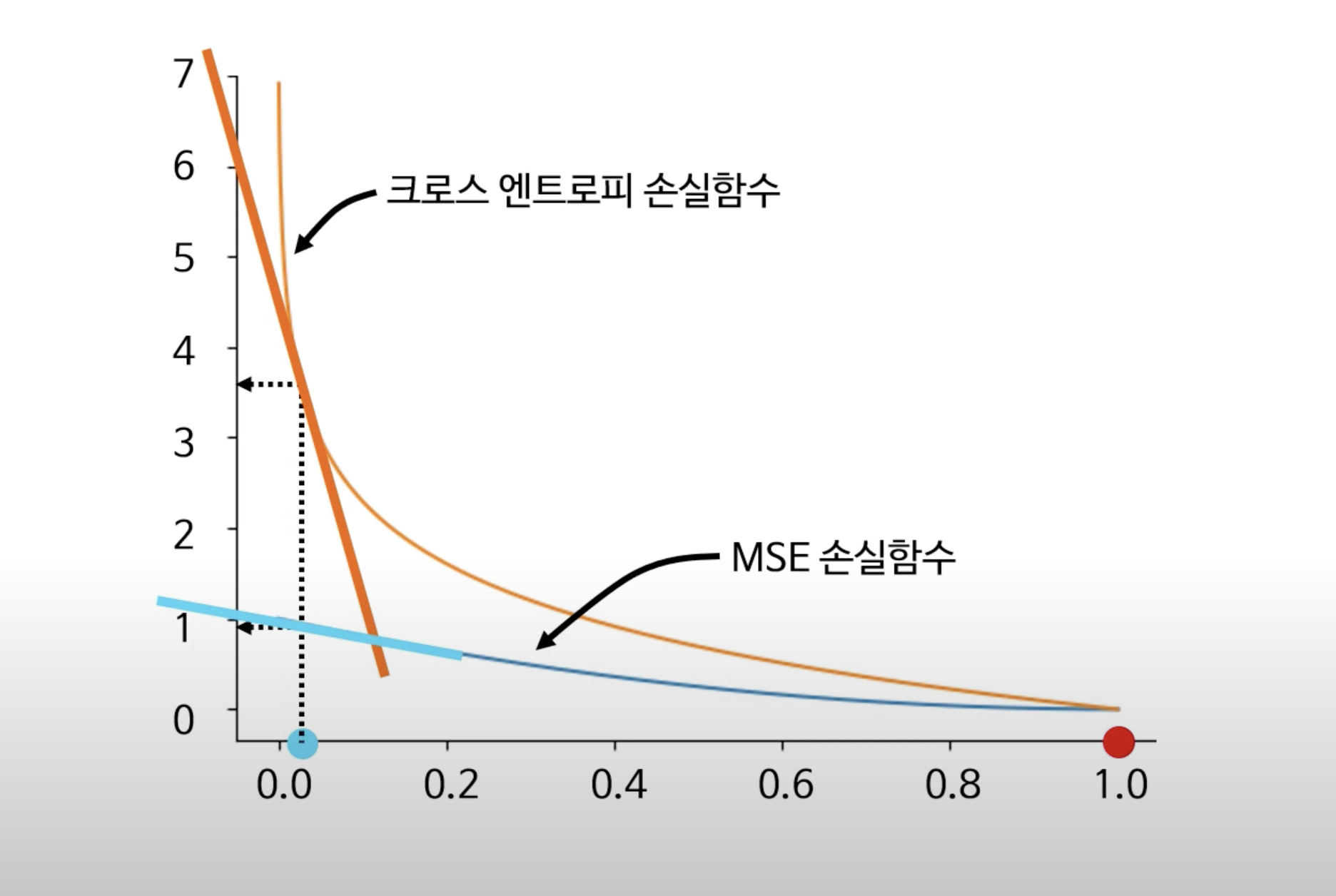
크로스 엔트로피가 MSE보다 더 좋은 이유는?
물론 MSE는 좋은 손실 함수이고, 직관적이고 쓰기 쉬운 함수이다.
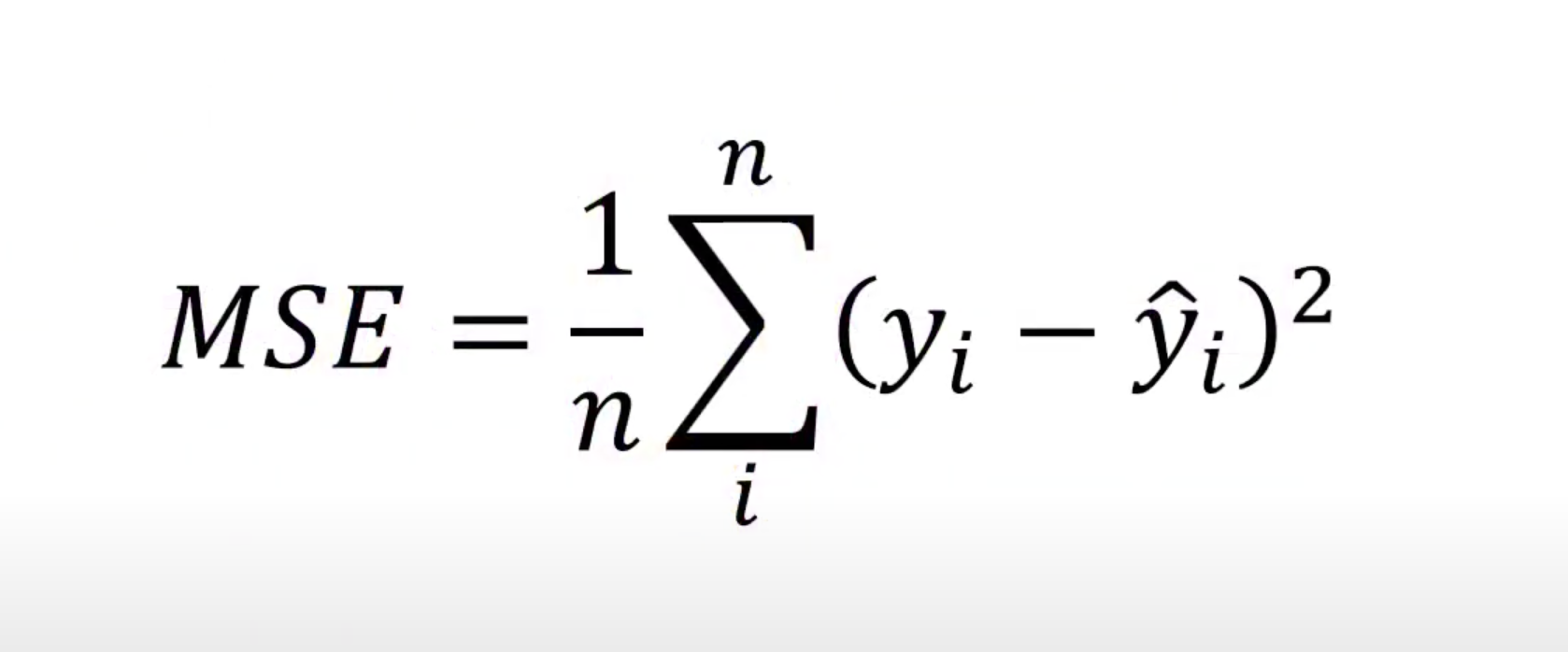
그러나, 크로스 엔트로피가 더 좋은 이유는 MSE보다 손실을 더 잘 보여주기 때문이다.
예측값이 실제 값에 비해 멀면 멀수록 크로스 엔트로피의 손실값이 MSE보다 크고, 기울기도 커서 크로스 엔트로피가 MSE에 비해 효율적으로 손실을 최소화 할 수 있다.