Angular-Spectrum Propagation

Fresnel 회절 적분은 convolution form 형태로 평가되는데

$U(x_2,y_2)=U(x_1,y_1) \ast [\cfrac{e^{ik\triangle z}}{i\lambda \triangle z}\ e^{i\frac{k}{2\triangle z}(x_1^2+y_1^2)}]$
$U(\mathbf{r_2})=U(\mathbf{r_1})\ \ast [\cfrac{e^{ik\triangle z}}{i\lambda\triangle z}e^{i\frac{k}{2\triangle z}\mathbf{r_1^2}}]$

2개의 FT를 이용하여 위 식 값을 결정하는데 convolution 정리를 씀.
$(x_1, y_1) → \mathbf{f_1} → (x_2,y_2)$

1. Fresnel 회절 적분의 angular spectrum 형태

$U(\mathbf{r}_2)=\mathcal{F}^{-1}[\mathbf{f_1}, \mathbf{r}_2]\ H(\mathbf{f_1})\ \mathcal{F}[\mathbf{r_1}, \mathbf{f_1}]\ \{U(\mathbf{r}_1)\}$

• $H(\mathbf{f_1})$ : free-space amplitude spread 함수(자유공간 전파의 transfer function)
• $H(\mathbf{f_1})=e^{ik\triangle z}e^{-i\pi\lambda\triangle z(f_{x1}^2+f_{y1}^2)}$

---

2. scaling 변수 도입

위의 convolution에서 $e^{ik\triangle z}$를 제외, $\mathbf{r_1}, \mathbf{r_2}$를 사용하여 적분식에 나타낸다.

$U(\mathbf{r_2})=\cfrac{1}{i\lambda\triangle z}\int\limits^{\infty}_{-\infty} U(\mathbf{r_1})\ e^{i\frac{k}{2\triangle z}|\mathbf{r}_2-\mathbf{r}_1|^2}d\mathbf{r_1}$

Tyler and Fried, Roberts만 scaling factor에 논의했다.
아래에서 $m$ scaling 도입

$|\mathbf{r_1}-\mathbf{r_2}|^2=r_2^2-2\mathbf{r}_2\cdot\mathbf{r_1}+r_1^2$
$=(r_2^2+\cfrac{r_2^2}{m}-\cfrac{r_2^2}{m})-2\mathbf{r}_2\cdot\mathbf{r}_1+(r_1^2+mr_1^2-mr_1^2)$
$=(r_2^2+(1-\cfrac{1}{m})\ r_2^2)-2\mathbf{r}_2\cdot\mathbf{r}_1+[mr_1^2+(1-m)r_1^2]$
$=m[(\cfrac{r_2}{m})^2-2(\cfrac{\mathbf{r_2}}{m})\cdot\mathbf{r_1}+r_1^2]+(1-\cfrac{1}{m})r_2^2+(1-m)r_1^2$
$=m|\cfrac{\mathbf{r}_2}{m}-\mathbf{r}_1|^2-(\cfrac{1-m}{m})\ r_2^2+(1-m)r_1^2$

이를 $U(\mathbf{r}_2)$에 대입

$U(\mathbf{r}_2)=\cfrac{e^{-i\frac{k}{2\triangle z}\frac{1-m}{m}r_2^2}}{i\lambda\triangle z}\int\limits^{\infty}_{-\infty} U(\mathbf{r_1})\ e^{i\frac{k}{2\triangle z}(1-m)r_1^2}\ e^{i\frac{km}{2\triangle z}\\ |\frac{\mathbf{r}_2}{m}-\mathbf{r}_1|^2}$

아래를 정의하고 위 식에 대입하면
$U^{''}(\mathbf{r_1})=\cfrac{1}{m}\ U(\mathbf{r_1})e^{i\frac{k}{2\triangle z}(1-m)r_1^2}$

$U(\mathbf{r_2})=\cfrac{e^{-i\frac{k}{2\triangle z}(\frac{1-m}{m})r_2^2}}{i\lambda z}\int\limits_{-\infty}^{\infty}mU^{''}(\mathbf{r_1})e^{i\frac{km}{2\triangle z}|\frac{\mathbf{r}_2}{m}-\mathbf{r_1}|^2}\ d\mathbf{r_1}$

scale된 좌표와 거리를 다음과 같이 정의하고
$\mathbf{r}_2'=\cfrac{\mathbf{r}_2}{m}$
$\triangle z'=\cfrac{\triangle z}{m}$

$U(∙)$ 식에 scale된 좌표 $\mathbf{r}_2=m\mathbf{r}_2'$

$U(m\mathbf{r_2'})=\cfrac{e^{-i\frac{k}{2\triangle z}m(1-m)(r_2')^2}}{i\lambda z}\int\limits_{-\infty}^{\infty}mU^{''}(\mathbf{r}_1)e^{i\frac{km}{2\triangle z}|\mathbf{r'_2}-\mathbf{r_1}|^2}d\mathbf{r}_1$

$\triangle z=\cfrac{\triangle z'}{m}$로 변환

$U(m\mathbf{r_2'})=\cfrac{e^{-i\frac{k}{2\triangle z'}(1-m)(r_2')^2}}{i\lambda z'}\int\limits_{-\infty}^{\infty}U^{''}(\mathbf{r}_1)e^{i\frac{k}{2\triangle z'}|\mathbf{r'_2}-\mathbf{r_1}|^2}d\mathbf{r}_1$

---

convolution 형태로 바꾸면
$U(m\mathbf{r_2'})=e^{-i\frac{k}{2\triangle z'}(1-m)(r_2')^2}\int\limits^{\infty}_{-\infty}U^{''}(\mathbf{r_1})\ h(\mathbf{r'_2}-\mathbf{r_1})\ d\mathbf{r}_1$
$h(\mathbf{r}_1)=\cfrac{1}{i\lambda \triangle z'}e^{i\frac{k}{2\triangle z'}r_1^2}$

propagation은 알려진 impulse response(amplitude spread function)를 가진 선형 시스템으로 취급할 수 있음

impulse response의 FT는 아래와 같은 amplitude transfer function이다.
$\mathcal{F}[\mathbf{r_1}, \mathbf{f_1}]h(\mathbf{r}_1)=H(\mathbf{f}_1)=e^{-i\pi\lambda\triangle z'f_1^2}$

convolution 정리를 사용하고, 원래의 좌표로 대체함으로써, 이 알고리즘 세부사항의 모든 detail을 유지하고 일부 단순화 가능

$U'(m\mathbf{r}'_2)=\mathcal{F}^{-1}[\mathbf{f_1,r_2']}\ e^{-i\pi\lambda\triangle z' f_1^2} \mathcal{F}[\mathbf{r_1}, \mathbf{f_1}]\{U^{''}(\mathbf{r}_1)\}$
$U'(\mathbf{r}_2)=\mathcal{F}^{-1}[\mathbf{f_1},\cfrac{\mathbf{r}_2}{m}]\ e^{-i\pi\lambda \frac{\triangle z}{m} f_1^2} \mathcal{F}[\mathbf{r_1}, \mathbf{f_1}]\{U^{''}(\mathbf{r}_1)\}$

$U(\mathbf{r}_2)=e^{-i\frac{km}{2\triangle z}(1-m)(\frac{\mathbf{r}_2}{m})^2}\ \mathcal{F}^{-1}[\mathbf{f_1},\cfrac{\mathbf{r_2}}{m}]\ e^{-i\pi\lambda\frac{\triangle z}{m}f_1^2} \mathcal{F}[\mathbf{r_1},\mathbf{f_1}]\{\cfrac{1}{m}U(\mathbf{r_1})e^{i\frac{k}{2\triangle z}(1-m)r_1^2}\}$
$=e^{-i\frac{k}{2\triangle z}\frac{1-m}{m}r_2^2}\ \mathcal{F}^{-1}[\mathbf{f_1}, \cfrac{\mathbf{r_2}}{m}]\ e^{-i\pi\lambda\frac{\triangle z}{m}f_1^2}\ \mathcal{F}[\mathbf{r_1,f_1]}\{\cfrac{1}{m}U(\mathbf{r_1)}\ e^{i\frac{k}{2\triangle z}(1-m)r_1^2}\}]$

$=\mathcal{Q}[\cfrac{-(1-m)}{m\triangle z}, \mathbf{r}_2]\ \mathcal{F}^{-1}[\mathbf{f}_1, \cfrac{\mathbf{r_2}}{m}]\ \mathcal{Q}_2[-\cfrac{\triangle z}{m},\mathbf{f}_1]\ \mathcal{F}[\mathbf{r_1}, \mathbf{f_1}]\ \mathcal{Q}[\cfrac{1-m}{\triangle z},\mathbf{r_1}] \{\cfrac{U(\mathbf{r_1})}{m}\}$

• $\mathcal{Q}[d,\mathbf{r}]\{U(\mathbf{r})\}≡ e^{i \frac{k}{2}c|\mathbf{r}|^2}\ U(\mathbf{r})$
• $\mathcal{Q}_2[d,\mathbf{r}]\{U(\mathbf{r})\}≡ e^{i\pi\lambda d |\mathbf{r}|^2}\ U(\mathbf{r})$

---

angular-spectrum propagation 연산자의 표현을 가지기 때문에 grid source 평면에서 grid spacing인 $\delta_1$, spatial-frequency 평면에서 $\delta_{f1}$, observation 평면에서 $\delta_2$를 구할 수 있다.

FT인 $\mathcal{F[\mathbf{r_1}, \mathbf{f_1}]}$로부터 얻는
$\delta_{f1}=\cfrac{1}{N\delta_1}$

inverse FT인 $\mathcal{F}^{-1}[\mathbf{f_1}, \mathbf{r_2}/m]$로부터 얻는
$\delta_{2}=\cfrac{m}{N\delta_{f1}}=\cfrac{m}{N(\frac{1}{N\delta_1})}=m\delta_1$
이를 통해 일관성을 확인 또한,
$\cfrac{1}{1-m}=\cfrac{1}{1-\frac{\delta_2}{\delta_1}}=\cfrac{\delta_1}{\delta_1-\delta_2}$

$\cfrac{m}{1-m}=\cfrac{\frac{\delta_2}{\delta_1}}{1-\frac{\delta_2}{\delta_1}}=\cfrac{\delta_2}{\delta_1-\delta_2}$

---

3. 다른 anglular-specturm 공식을 위한 solution

$|\mathbf{r}_2-\mathbf{r}_1|^2=r_2^2- 2\mathbf{r}_2 \cdot \mathbf{r}_1+r_1^2$
$=(r_2^2+\cfrac{r_2^2}{m}-\cfrac{r_2^2}{m})-2\mathbf{r}_2\cdot\mathbf{r}_1+(r_1^2+mr_1^2-mr_1^2)$
$=-\cfrac{r_2^2}{m}+(1+\cfrac{1}{m})r_2^2-2\mathbf{r_2}\cdot\mathbf{r_1}-mr_1^2+(1+m)r_1^2$

$=-\cfrac{r_2^2}{m}-2\mathbf{r_2}\cdot\mathbf{r_1}-mr_1^2+(1+\cfrac{1}{m})r_2^2+(1+m)r_1^2$
$=-m(|\cfrac{\mathbf{r_2}}{m}|^2+2(\cfrac{\mathbf{r_2}}{m})\cdot\mathbf{r_1}+r_1^2)+(1+\cfrac{1}{m})r_2^2+(1+m)r_1^2$
$=-m|\cfrac{\mathbf{r_2}}{m}+\mathbf{r_1}|^2+(\cfrac{1+m}{m})r_2^2+(1+m)r_1^2$

$m'=-m$로 치환
$=m'|\cfrac{\mathbf{r_2}}{-m'}+\mathbf{r}_1|^2+(\cfrac{1-m'}{-m'})r_2^2+(1-m')r_1^2$
$=m'|\cfrac{\mathbf{r_2}}{m'}-\mathbf{r}_1|^2-(\cfrac{1-m'}{m'})r_2^2+(1-m')r_1^2$
여기서
$m'$ 대신에 $m$을 사용하면 원래 맨 위에 증명식하고 같아짐.

---

Angular-spectrum 형태의 회절을 $±m$을 사용하여 구현한다면 2가지 식이 있음.

1. $U(\mathbf{r}_2)=\mathcal{Q}[\cfrac{m-1}{m\triangle z},\mathbf{r_2}]\ \mathcal{F}^{-1}[\mathbf{f_1}, \cfrac{\mathbf{r_2}}{m}]\ \mathcal{Q}_2[-\cfrac{\triangle z}{m}, \mathbf{f}_1] \times \mathcal{F}[\mathbf{r_1}, \mathbf{f_1}]\ \mathcal{Q}[\cfrac{1-m}{\triangle z}, \mathbf{r_1}]\ \cfrac{1}{m} \{U(\mathbf{r_1})\}$

2. $U(\mathbf{r}_2)=\mathcal{Q}[\cfrac{-m-1}{-m\triangle z},\mathbf{r}_2]\ \mathcal{F}^{-1}[\mathbf{f}_1,\cfrac{\mathbf{r_2}}{-m}]\ \mathcal{Q}_2[\cfrac{\triangle z}{m},\mathbf{f}_1]\times\mathcal{F}[\mathbf{r_1}, \mathbf{f_1}]\ \mathcal{Q}[\cfrac{1+m}{\triangle z}, \mathbf{r_1}]\ (\cfrac{-1}{m}) \{U(\mathbf{r_1})\}$

이를 한번에 식을 쓰면,
$U(\mathbf{r}_2)=\mathcal{Q}[\cfrac{m±1}{m\triangle z},\mathbf{r}_2]\ \mathcal{F}^{-1}[\mathbf{f}_1,∓\cfrac{\mathbf{r_2}}{m}]\ \mathcal{Q}_2[±\cfrac{\triangle z}{m},\mathbf{f}_1]\times\mathcal{F}[\mathbf{r_1}, \mathbf{f_1}]\ \mathcal{Q}[\cfrac{1±m}{\triangle z}, \mathbf{r_1}]\ (∓\cfrac{1}{m}) \{U(\mathbf{r_1})\}$

---

4. 코드 구현

4.1 함수 정의

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import fresnel


def ang_spec_prop(Uin, wavelength, d1, d2, distance):
    k = 2*np.pi/wavelength

    # source-plane coordinates
    sc = np.arange(-N/2, N/2)*d1
    x1, y1 = np.meshgrid(sc,sc);
    r1sq = x1**2+y1**2

    # spatial frequencies (of source plane)
    df1 = 1 / (N*d1)
    fc = np.arange(-N/2, N/2)*df1
    fX, fY = np.meshgrid(fc,fc)
    fsq = fX**2+fY**2
    
    # magnification
    m = d2/d1
    
    # observation-plane coordinates
    oc = np.arange(-N/2, N/2)*d2
    x2, y2 = np.meshgrid(oc, oc)
    r2sq = x2**2+y2**2

    # quadratic phase factors
    Q1 = np.exp(1j*k*(1-m)/(2*distance) *r1sq)
    Q2 = np.exp(-1j*2*np.pi**2*distance/(m*k) *fsq)
    Q3 = np.exp(1j*k/2*(m-1)/(m*distance) *r2sq)

    # compute the propagated field
    Uout = Q3*np.fft.ifft2(Q2*np.fft.fft2(Q1*Uin/m))
    
    return x2, y2, Uout

def rect(x, a):
    tmp = np.where(np.abs(x) < a/2, 1, 0)
    return np.where(np.abs(tmp)==a/2, 0.5, tmp) 

def fresnel_prop_square_ap(x2, y2, D1, wavelength, distance):
    N_F = (D1/2)**2 / (wavelength * distance) # Fresnel number

    # substitutions
    bigX = x2 / np.sqrt(wavelength*distance)
    bigY = y2 / np.sqrt(wavelength*distance)
    alpha1 = -np.sqrt(2)*(np.sqrt(N_F)+bigX)
    alpha2 = np.sqrt(2)*(np.sqrt(N_F) -bigX)
    beta1  = -np.sqrt(2)*(np.sqrt(N_F)+bigY)
    beta2  = np.sqrt(2)*(np.sqrt(N_F)-bigY)
    # Fresnel sine and cosine integrals
    ca1, sa1 = fresnel(alpha1);
    ca2, sa2 = fresnel(alpha2);
    cb1, sb1 = fresnel(beta1);
    cb2, sb2 = fresnel(beta2);
    # observation-plane field
    U = 1/(2*1j)*((ca2-ca1)+1j*(sa2-sa1))*((cb2-cb1)+1j*(sb2-sb1))
    
    return U

4.2 전파 시뮬레이션

N=1024  # number of grid points per side
L=1e-2  # total size of the grid[m]
delta1 = L/N # grid spacing [m]
D = 2e-3 # diameter of the aperture [m]
wavelength = 1e-6 # optical wavelength [m]
k = 2*np.pi / wavelength
distance = 1 # propagation distance [m]

sc = np.arange(-N/2, N/2)*delta1
x1, y1 = np.meshgrid(sc,sc)
aperture = rect(x1,D)*rect(y1,D)

delta2 = wavelength * distance / (N*delta1)
x2, y2, Uout = ang_spec_prop(aperture, wavelength, delta1, delta2, distance)

# analytic result for y2=0 slice
Uout_an = fresnel_prop_square_ap(x2[int(N/2)+1], 0, D, wavelength, distance)
Uout_an2 = fresnel_prop_square_ap(x2, y2, D, wavelength, distance)

Uout_shift = np.fft.fftshift(Uout)

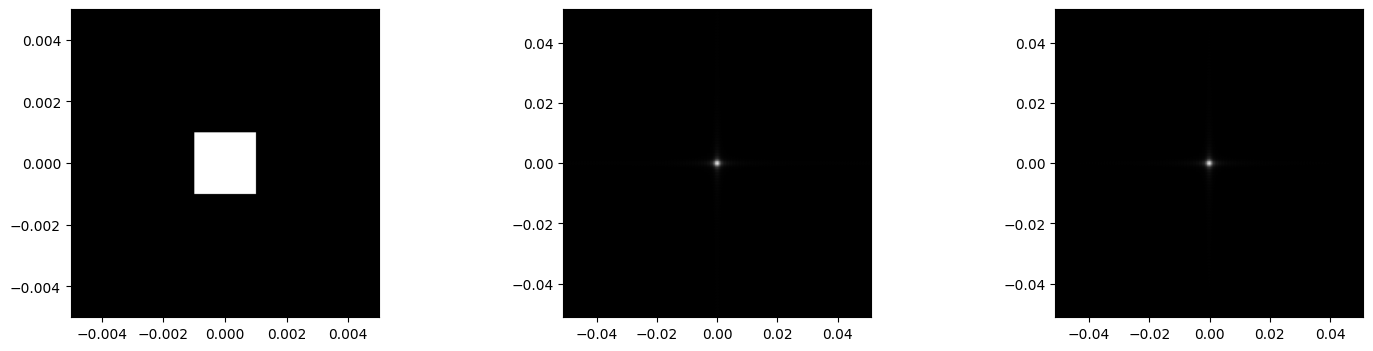
plt.figure(figsize=(18,4))
plt.subplot(1,3,1)
plt.imshow(np.abs(aperture), cmap='gray', extent=(x1.min(),x1.max(), y1.min(),y1.max()))
plt.subplot(1,3,2)
plt.imshow(np.abs(Uout_shift), cmap='gray', extent=(x2.min(), x2.max(), y2.min(), y2.max()))
plt.subplot(1,3,3)
plt.imshow(np.abs(Uout_an2), cmap='gray', extent=(x2.min(), x2.max(), y2.min(), y2.max()))
plt.show()

4.3 단면 시각화

plt.figure(figsize=(16,6))
plt.subplot(1,2,1)
plt.xlim(-0.003,0.003)
plt.ylim(0,2.5)
plt.plot(x2[1], np.abs(Uout_an**2), marker='s')
plt.plot(x2[1], np.abs(Uout_shift[int(N/2)])**2, marker='x')

plt.subplot(1,2,2)
plt.xlim(-0.003,0.003)
plt.plot(x2[1], np.angle(Uout_an), marker='s')
plt.plot(x2[1], np.angle(Uout_shift[int(len(Uout_shift)/2)]), marker='x')
plt.show()