Point Sources Propagation

point source를 모델링하기에는 어렵다.

실제 point source $U_{pt}(\mathbf{r_1})$는 dirac delta 함수에 의해 표현되는데, 이때 $x_1, y_1$ 평면에서 point source 위치는 $\mathbf{r}_c=(x_c,y_c)$이다.

$U_{pt}(\mathbf{r}_1)=\delta(\mathbf{r}_1-\mathbf{r}_c)$

$U_{pt}(\mathbf{r}_1)$은 모든 공간 주파수에서 일정한 값의 Fourier spectrum을 갖는다.
이것은 무한대한 공간 대역폭를 가진다는 의미이고, 반면에 모든 optical source들이 공간적으로 대역폭이 제한되어 있기 때문에 비이상적이다.
무한한 공간 대역폭은 컴퓨터로 시뮬레이션 해서 이산적으로 샘플되고 유한 사이즈의 grid로 인한 문제가 있다.

만약 전파 시 source 평면에서 spacing이 $\delta_1$이면, grid에서 aliasing 없이 표현되는 가장 높은 신호의 공간 주파수는 $\cfrac{1}{2\delta_1}$이다.

$f_s>2f_{max}$
sampling 주파수가 신호의 최대 주파수보다 커야 한다.

그러므로 점 광원의 대역폭 제한 버전이 충분해야 한다.
point source는 유한한 공간적 확장을 가져야 한다.

다양한 point-source model이 사용되는데

1. turbulence 전파를 시뮬레이션하기 위해 2차 위상을 가진 좁은 Gaussian function을 사용(Martin and Flatte, Coles)

   • $\sigma$, $x_0$: grid spacing
   • $\exp(-\cfrac{r^2}{2\sigma^2})\exp(-i\cfrac{r^2}{2x_0^2})$

2. 시뮬레이션에서 경계 흡수를 사용하여, 이 모델은 observation 평면 field를 만들고 edge로 갈수록 0으로 수렴하며, propgation grid의 중심에서 1/3지점까지 flat하다.

3. 후에 Flatte는 point source field를 grid spacing과 거의 동등한 $\sigma$, $\rho$. observation 평면 grid의 중심에서 1/3까지 거의 flat하고 edge로 갈수록 0으로 수렴한다.

   • $\exp(\cfrac{r^2}{2\sigma^2})\ \cos(\cfrac{r^2}{2\rho^2})$

4. 다른 접근법은 source로부터 $\triangle z$만큼 떨어진 위치의 $x_2-y_2$ 평면에서 관측하는 경우, 우리는 observation field를 다음과 같이 쉽게 구할 수 있다.

$U(\mathbf{r}_2)=\cfrac{e^{ik\triangle z}}{i\lambda\triangle z}e^{i\frac{k}{2\triangle z}|\mathbf{r}_2-\mathbf{r}_c|^2}$

이 결과는 구면파로 근축 근사한 것이고, $x_2-y_2$ 평면에서는 동일한 진폭과 parabolic(2차) 위상을 갖는다.

우리의 목표는 simulation과 향후 실험 간 좋은 일치를 얻는 것이다.
어떤 camera 또는 wavefront sensor 센서를 사용할 때, 그것은 오직 유한한 영역의 $x_2-y_2$ 평면을 차지한다.
따라서 시뮬레이션이 detector 영역 전체에서 좋은 일치를 얻으면 source model이 유효하다.
field $\tilde{U}(\mathbf{r}_2)$가 유한한 spatial extent(공간적 영역)를 가졌을 때, $W(\mathbf{r}_2)$는 공간의 유한한 영역에서만 0이 아닌 window 함수이다.
$W(\mathbf{r}_2)$의 범위는 detector보다는 크고, propagation grid보다는 작아야한다. ex). 2D rect, circ 함수

$\tilde{U}(\mathbf{r}_2)=\cfrac{e^{ik\triangle z}}{i\lambda \triangle z}\ W(\mathbf{r}_2-\mathbf{r}_c)\ e^{i\frac{k}{2\triangle z}|\mathbf{r}_2-\mathbf{r}_c|^2}$

---

$\tilde{U}_{pt}(\mathbf{r}_1)$에 의한 point-source 모델을 나타내면, Fresnel 회절 적분으로 대체하면, $\tilde{U}(\mathbf{r}_2)$와 같은 결과로 맞춘다.

$\tilde{U}(\mathbf{r}_2)=\cfrac{e^{ik\triangle z}}{i\lambda \triangle z}\ e^{i\frac{k}{2\triangle z}r_2^2}\int\limits_{\infty}^{\infty}\tilde{U}_{pt}(\mathbf{r}_1)e^{i\frac{k}{2\triangle z}r_1^2}\ e^{-i\frac{2\pi}{\lambda \triangle z}\mathbf{r}_1\cdot\mathbf{r}_2}\ d\mathbf{r}_1$
$=\cfrac{e^{ik\triangle z}}{i\lambda \triangle z}e^{i\frac{k}{2\triangle z}r_2^2}\mathcal{F}\{\tilde{U}_{pt}(\mathbf{r}_1)e^{i\frac{k}{2\triangle z}r_1^2}\}_{\mathbf{f}_1=\frac{\mathbf{r_2}}{\lambda\triangle z}}$

따라서 point-source model은
$\tilde{U}_{pt}(\mathbf{r}_1)=i\lambda\triangle ze^{-ik\triangle z}e^{-i\frac{k}{2\triangle z}r_1^2}\mathcal{F}^{-1}\{\tilde{U}(\lambda\triangle z\mathbf{f}_1)e^{-i\pi\lambda\triangle z f_1^2}\}$

$\tilde{U}(\lambda\triangle z\mathbf{f}_1)=\cfrac{e^{ik\triangle z}}{i\lambda\triangle z}\ W(\lambda\triangle z\mathbf{f}_1-\mathbf{r}_c)e^{i\frac{k}{2\triangle z}|\lambda\triangle z\mathbf{f}_1-\mathbf{r}_c|^2}$
$=\cfrac{e^{ik\triangle z}}{i\lambda\triangle z}\ W(\lambda\triangle z\mathbf{f}_1-\mathbf{r}_c)e^{i\pi\lambda\triangle z f_1^2-i2\pi\mathbf{f}_1\mathbf{r}_c+i\frac{k}{2\triangle z}r_c^2}$를 위에 point-source model에 대입

$\tilde{U}_{pt}(\mathbf{r}_1)=e^{-ik\frac{k}{2\triangle z}r_1^2}e^{i\frac{k}{2\triangle z}r_c^2}\mathcal{F}^{-1}\{W(\lambda\triangle z\mathbf{f}_1-\mathbf{r}_c)e^{-i2\pi\mathbf{r}_c\cdot\mathbf{f}_1}\}$

예를 들어, 너비가 D인 정사각형 영역을 사용한다고 하면,
$W(\mathbf{r}_2-\mathbf{r}_c)=A\ rect(\cfrac{x_2-x_c}{D})\ rect(\cfrac{y_2-y_c}{D})$
위의 $\tilde{U}_{pt}(\mathbf{r}_1)$이 A의 진폭을 갖는다고 하면 point source 모델은

$\tilde{U}_{pt}(\mathbf{r}_1)=Ae^{-ik\frac{k}{2\triangle z}r_1^2}e^{i\frac{k}{2\triangle z}r_c^2}\times \mathcal{F}^{-1}\{rect(\cfrac{\lambda\triangle z f_x - x_c}{D})\ rect(\cfrac{\lambda\triangle z f_y - y_c}{D}) e^{-i2\pi\mathbf{r}_c\cdot\mathbf{f}_1}\}$

$=Ae^{-ik\frac{k}{2\triangle z}r_1^2}e^{i\frac{k}{2\triangle z}r_c^2} e^{-i\frac{k}{\triangle z}\mathbf{r}_c\cdot\mathbf{r}_1}\times (\cfrac{D}{\lambda\triangle z})^2\ sinc[\cfrac{D(x_1-x_c)}{\lambda\triangle z}]\ sinc[\cfrac{D(y_1-y_c)}{\lambda\triangle z}]$

code에 사용된 point source 모델은 아래 그림

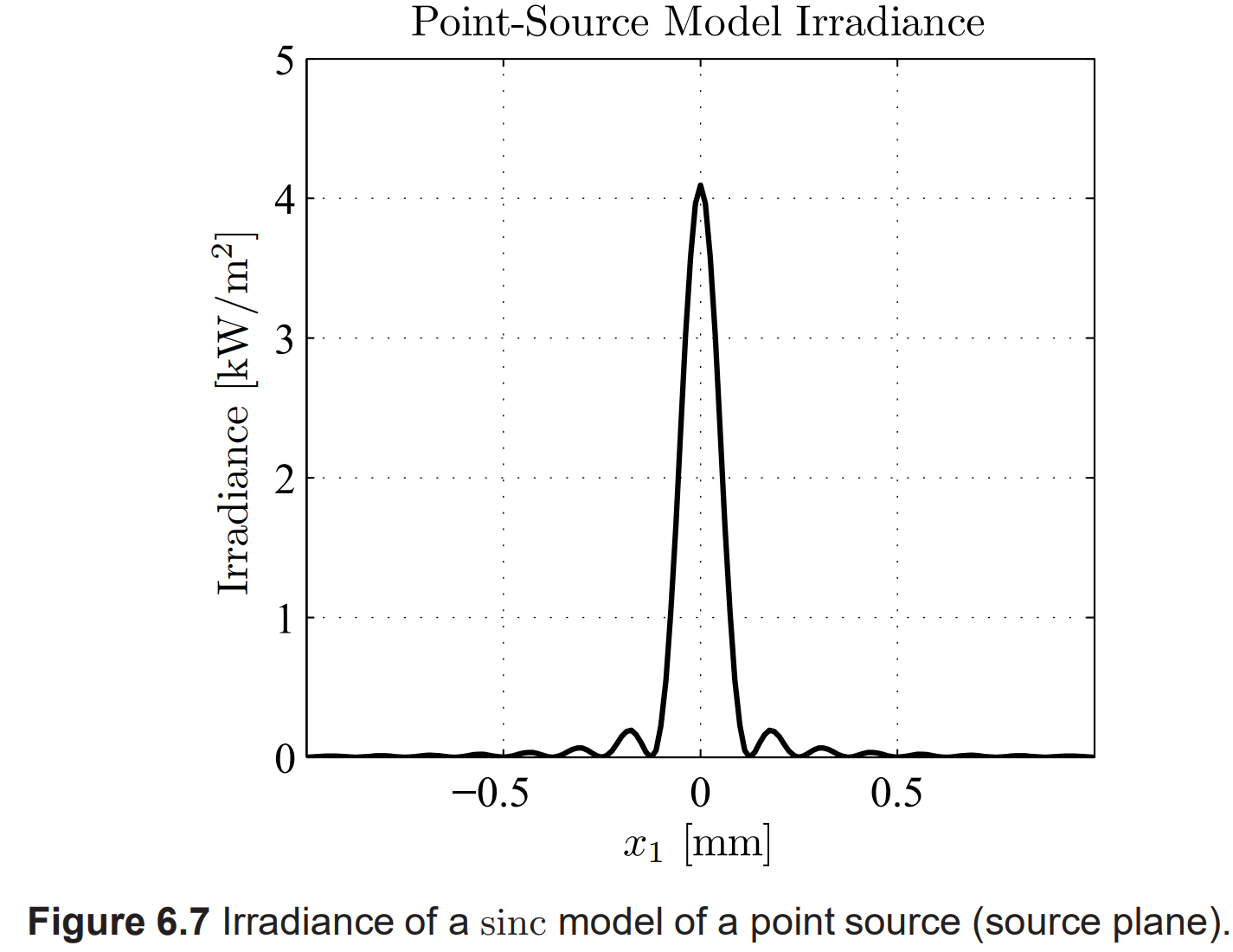
grid spacing이 중앙 lobe을 가로질러 10개의 grid point가 있도록 설정. 이는 점처럼 보이지 않을 수 있지만,

• 실제로 직경이 0.125mm에 불과. 이는 8.0mm에 이르는 윈도우 함수보다 훨씬 좁고,
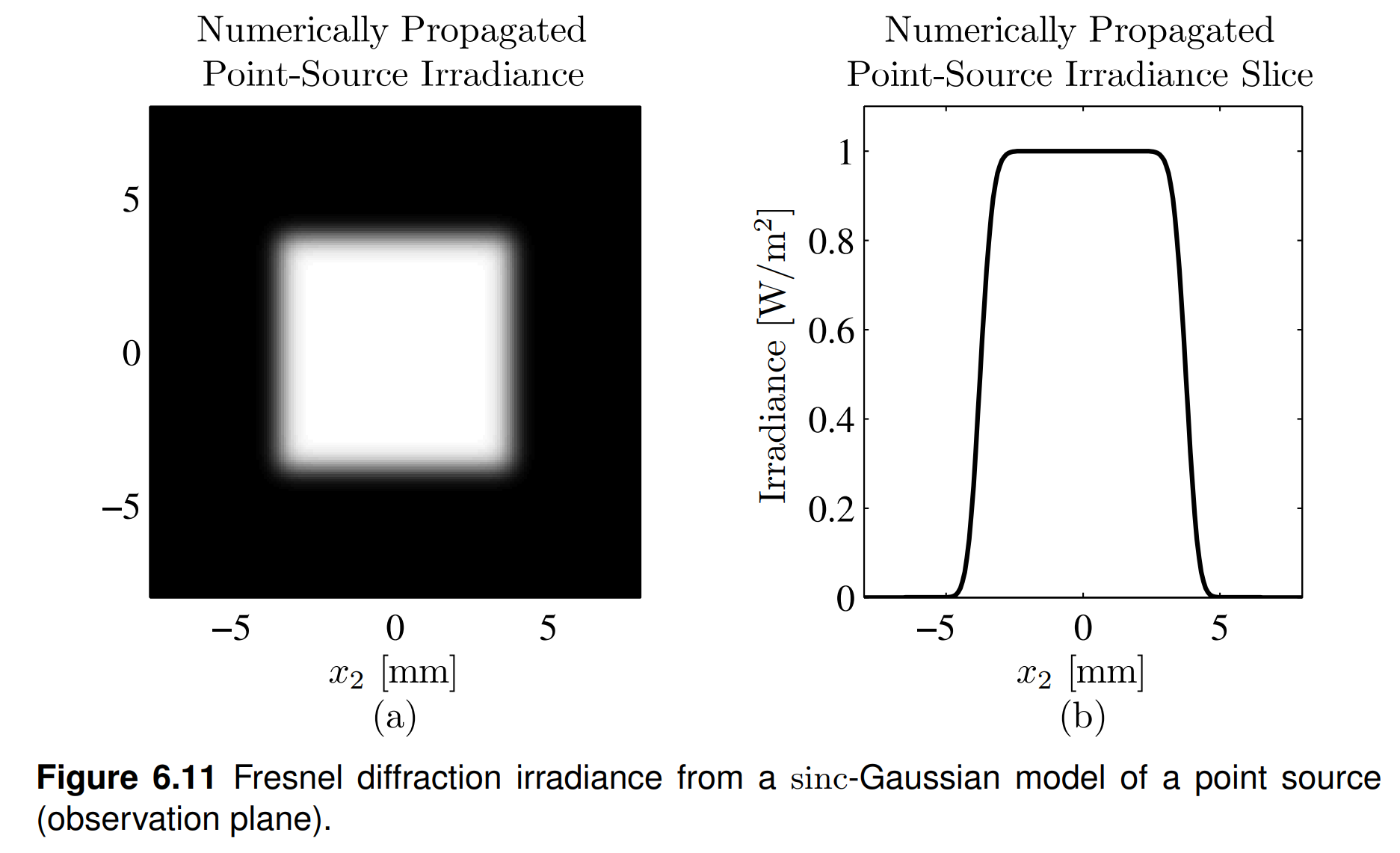
• observation plane에서 강도
  

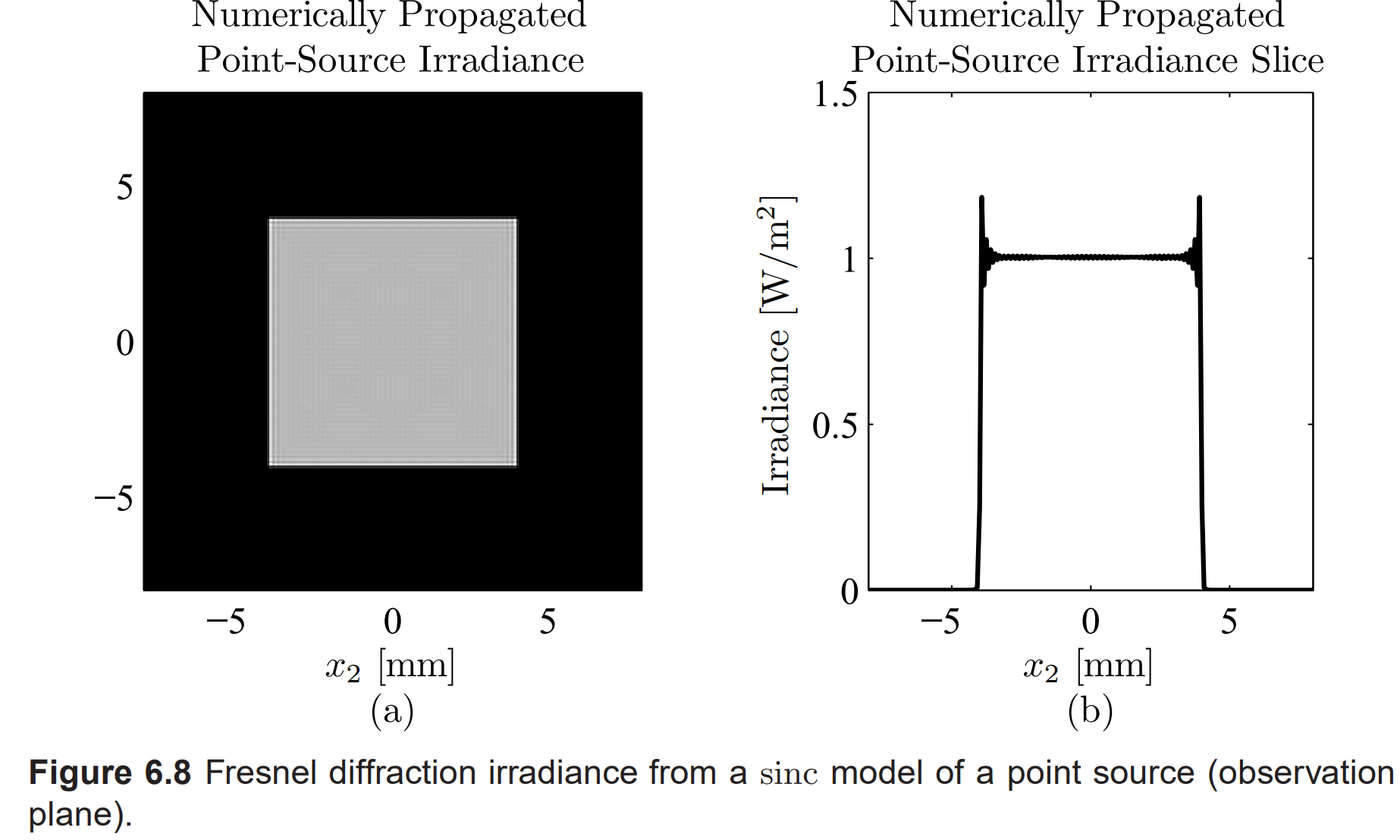
window의 효과는 두 그래프 모두에서 명확히 나타나며, point source model은 ROI 내의 observation 평면에서 정확히 원하는 것을 생성. 이 모델이 제 9.5절에서 난류 시뮬레이션에 사용될 때 point source model의 매개 변수 D는 관측 망원경의 지름보다 네 배 크게 설정. 이렇게 함으로써 난류의 변동이 window 가장자리가 망원경에 의해 관측되는 것을 방지.

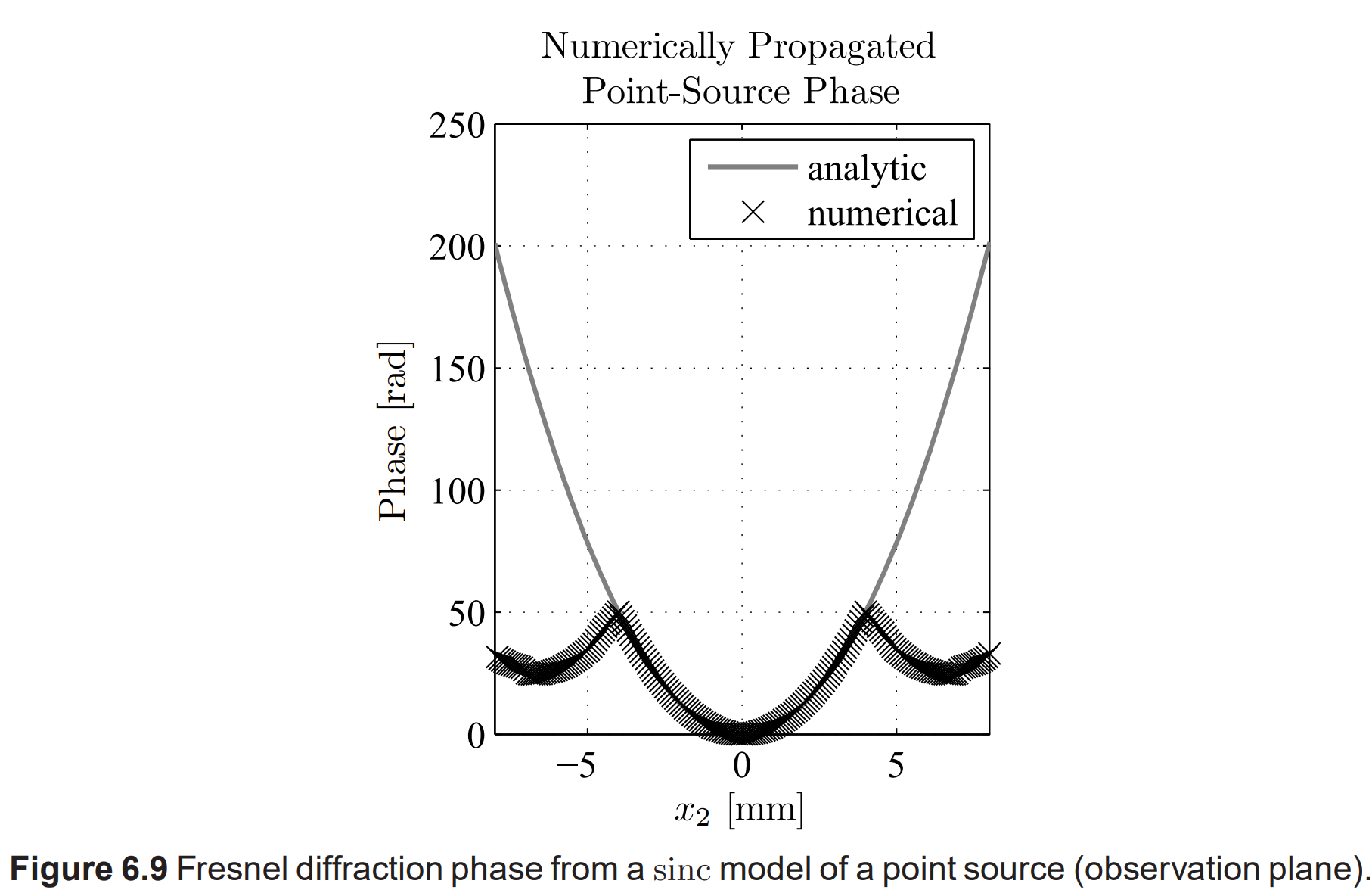
ROI 밖에서 aliasing이 나타남.
point source model 수정이 일부 aliasing을 완화하게끔.

---

Martin과 Flatté의 접근 방식과 Flatté 등의 접근 방식은 사용하는 가우시안 모델 때문에 이러한 문제가 없다.
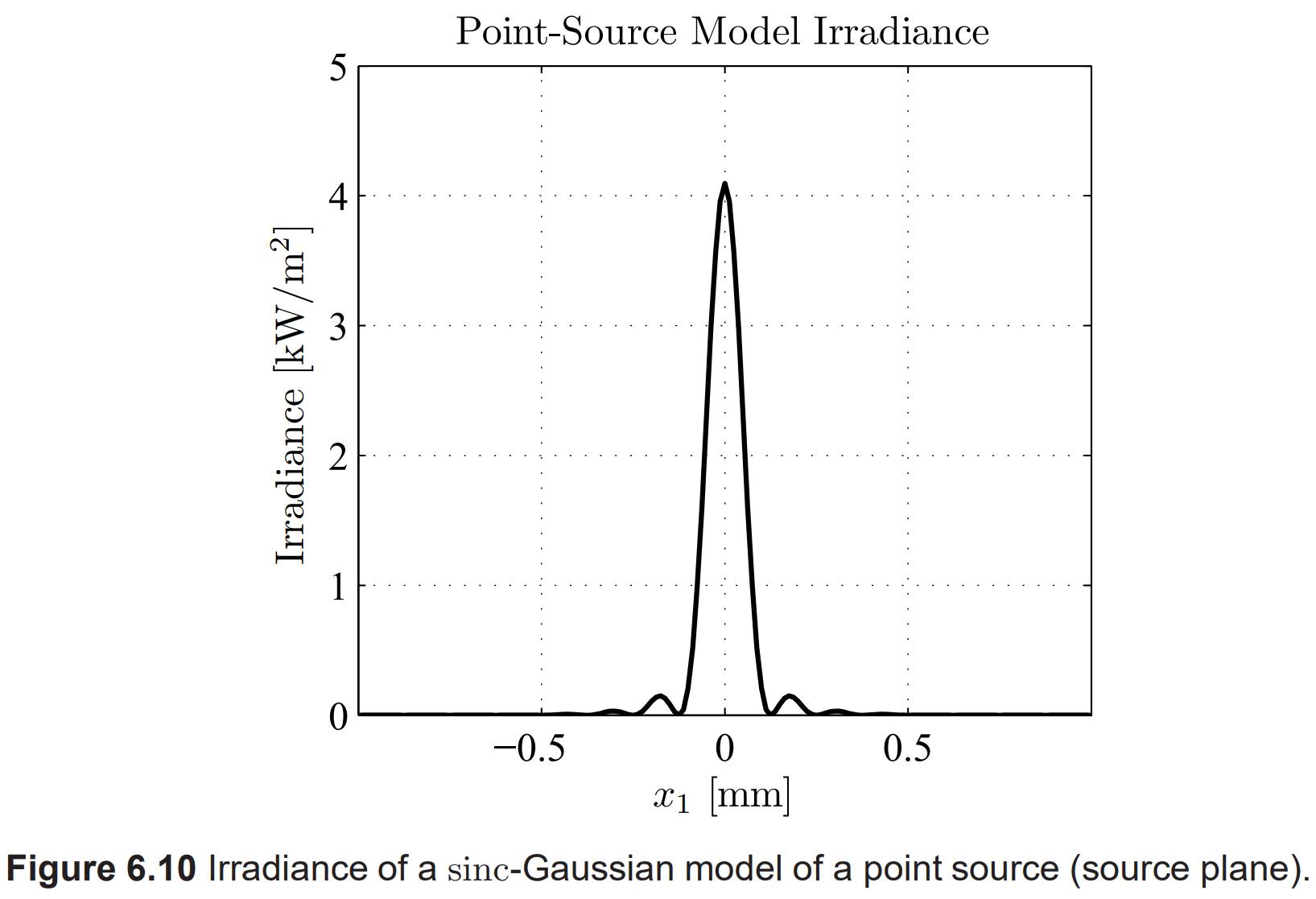
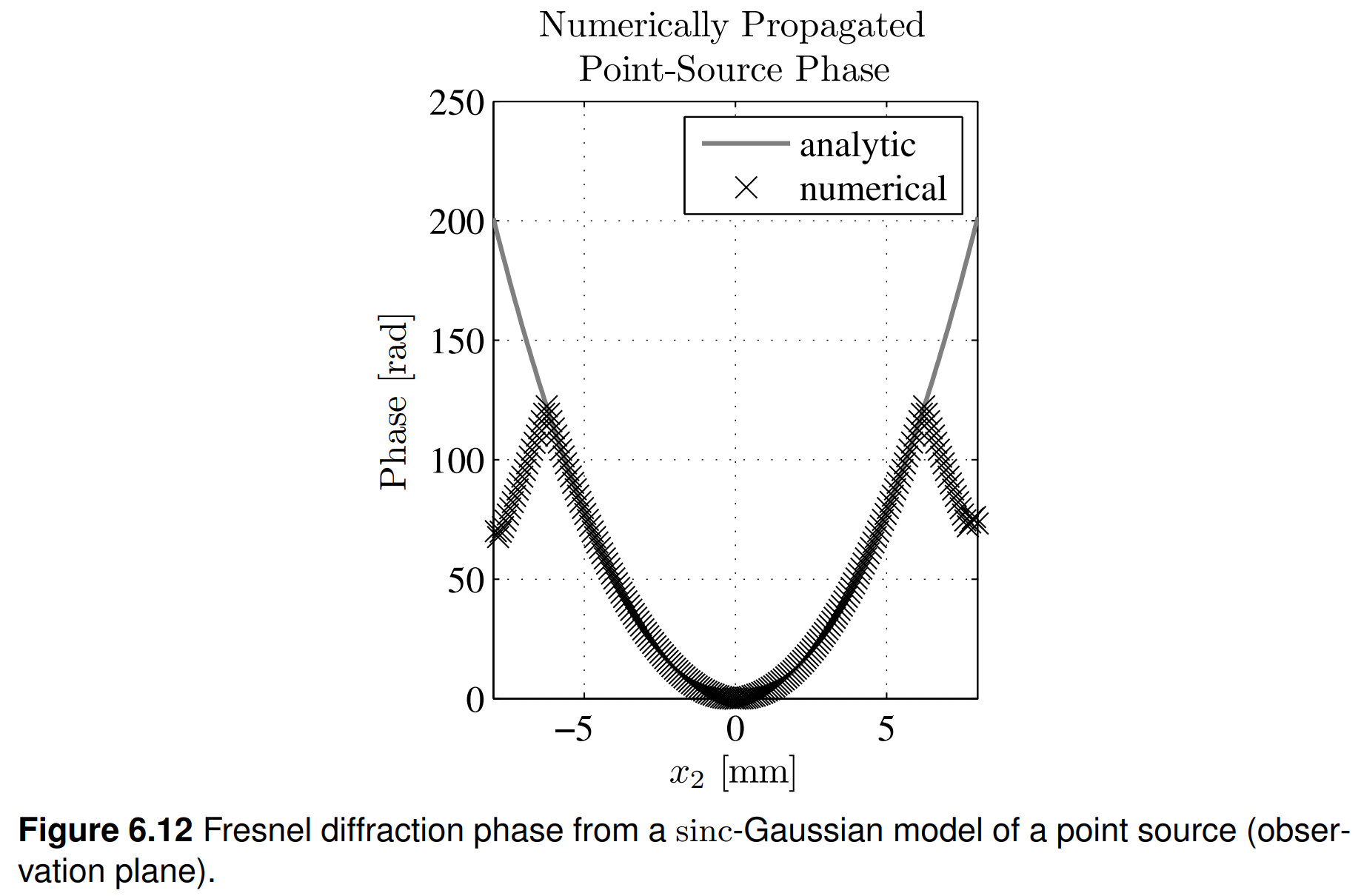
사실, sinc와 가우시안 포인트 소스 모델을 결합하면 phase 에일리어싱이 약간 줄어듭니다. 설명을 위해, Listing 6.9에서 이를 구현합니다. 코드는 Listing 6.8과 매우 유사하지만 모델 포인트 소스가 17번째 줄에서 가우시안 함수로 곱해집니다. sinc-가우시안 모델 포인트 소스와 결과적인 관측 평면 필드는 Fig. 6.10–6.12에 표시됩니다. Fig. 6.7과 6.10을 비교하면 가우시안 요소가 모델 포인트 소스의 측면 로브를 줄이고 이로 인해 관측 평면 필드의 입사 프로파일을 부드럽게하는 것이 분명합니다. 또한 그리드의 가장자리쪽에서 계산된 관측 평면 위상은 Fig. 6.12에서 분석적 위상과 훨씬 더 일치합니다.