진공에서 Fresnel 회절

signer do·2024년 5월 8일

Optical Wave Propagation 수치 시뮬레이션

목록 보기

4/12

여기서는 near-field(근거리) optical wave 전파에 대해 높은 정확도와 유연함을 가지고 모델링하는 기법을 소개한다.
원거리 전파보다는 상당히 더 어렵다.

Fresnel 회절 적분과 다른 형태로 다른 방법으로 수치적으로 계산되며 각 장점과 단점을 논의한다.

다른 수학적 모델에서의 기호, 연산자를 강조하고 나머지는 기본 알고리즘에 대해 소개한다.

Fresnel 회절 적분안에 quadratic phase factor(2차 위상)은 대역이 제한되지 않는다(무한대 적분이라서). 이것은 sampling과 관계된 어려움을 가져온다.
적분을 계산하기 위해서는 single FT 또는 convolution과 같은 것을 사용.

예를 들어, Delen과 Hooker는 적분된 광학적 구성요소에서 전파 시뮬레이션에 유용한 방법을 제안.

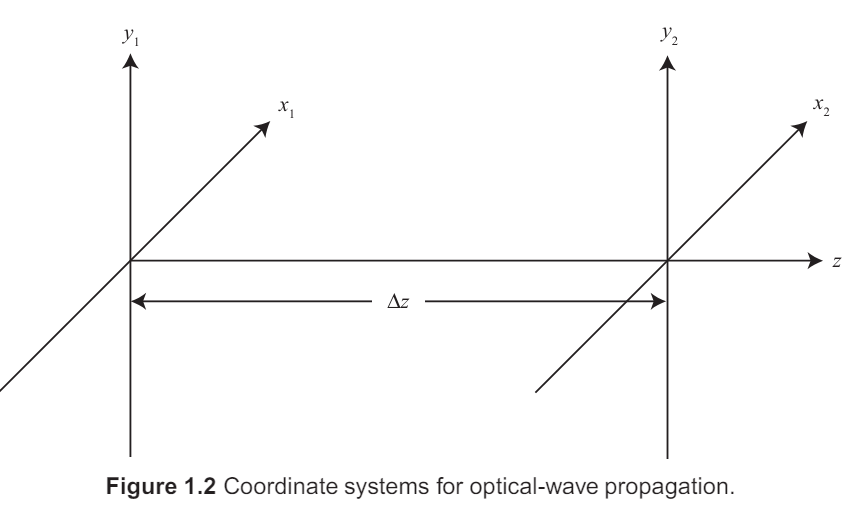
이 구성요소들의 interface들은 종종 비스듬히 기울거나 offset 그리고 각도들이 항상 광축이 아니기 때문에 Rayleigh-Summerfeld 전파 방법을 개발하여 임의의 배치된 plane 사이에서의 전파를 높은 정확도로 다룸.

원거리 전파일 때는, 광축 근사가 좋은 방법인데, beam이 원래 크기보다 더 크게 퍼진다. 그에 맞춰, 몇몇 알고리즘들은 observation과 source plane grid spacing 사이의 scailing 값을 선택할 수 있는 유연함을 제공한다.

Tyler and Fried
Roberts
Coles
Rubio
Deng et al
Coy(Two-step Propagation)
Rydberg and Bengtsson(Two-step Propagation)
Voelz and Roggemann

수학적으로는 똑같지만, Coles에 의해 소개된 알고리즘과 후에 보충된 Rubio 알고리즘은 발산하는 구형 좌표계를 각 grid를 사용하여 일정한 각 grid spacing을 이용했다.
점 광원일 경우 특히 사용한다.
Rubio는 이 기본 컨셉에서 매우 긴 전파거리도 보강했다.
grid는 field를 충분히 sample하기에 크게 자라기 때문에, Rubio 방법은 중심 부분을 뽑고 더 세밀한 grid를 interpolate한다.

2개의 유연한 전파 방법을 소개하고,
1. Fresnel diffraction integral을 2단계로 계산 한다.
2. Fresnel 회절 적분의 convolution 형태를 대수적 조작하여 사용한다. free parameter를 도입하여 observation-plane의 grid spacing을 직접 설정할 수 있다.

1. Fresnel 회절 적분의 2가지 형태

1.1 Fresnel 전파에서의 기호 정리

기호	의미
$\mathbf{r}_1=(x_1,y_1)$	source 평면 좌표
$\mathbf{r}_2=(x_2,y_2)$	observation 평면 좌표
$\mathbf{r}_2=(x_2,y_2)$	observation 평면 좌표
$\delta_1$	source 평면의 grid spacing
$\delta_2$	observation 평면의 grid spacing
$\mathbf{f}_1=(f_{x1},f_{x2})$	source 평면의 공간 주파수
$\delta_{f1}$	source 평면 공간 주파수에서 grid spacing
$z_1$	광축에 따라 source 평면 위치
$z_1$	광축에 따라 observation 평면 위치
$\triangle z$	source과 observation 평면 사이 거리
$m$	source에서 observation 평면까지 배율 인자

1.2 Fresnel 적분

$U(x_2, y_2)=\cfrac{e^{ik\triangle z}}{i\lambda\triangle z}\ \int\limits^{\infty}_{-\infty} \int\limits^{\infty}_{-\infty}\ U(x_1, y_1)\ e^{i \frac{k}{2\triangle z}[(x_2-x_1)^2+(y_2-y_1)^2]}\ dx_1\ dy_1$

공간 vector와 공간 주파수 vector를 다음과 같이 정의.
1. source 평면: $\mathbf{r}_1 = x_1 \hat\mathbf{i} + y_1 \hat\mathbf{j}$
2. observation 평면: $\mathbf{r}_2 = x_2 \hat\mathbf{i} + y_2 \hat\mathbf{j}$
3. $\mathbf{f}_1 = f_{x1} \hat\mathbf{i} + f_{y1} \hat\mathbf{j}$

source-plane field의 지식으로부터 observation optical field를 계산하기 위해 Fresnel 회절 적분을 사용하고 싶다. 위의 식은 2가지 형태가 있는데.

지수의 제곱항을 전개하고 적분 내의 지수항을 인수분해하면 아래와 같다.
$U(x_2, y_2)=\cfrac{e^{ik\triangle z}}{i\lambda\triangle z}\ e^{i\frac{k}{2\triangle z}(x^2_2+y_2^2)}\times \int\limits^{\infty}_{-\infty} \int\limits^{\infty}_{-\infty}\ U(x_1, y_1)\ e^{i \frac{k}{2\triangle z}(x_1^2+y_1^2)}\ e^{-i\frac{2\pi}{\lambda\triangle z}(x_2x_1+y_2y_1)}\ dx_1\ dy_1$
이것은 FT로 계산할 수 있다.
source-plane field ( $U(x_1,y_1)$ )와 free-space 진폭 spread 함수( $\cfrac{e^{ik\triangle z}}{i\lambda \triangle z}\ e^{i\frac{k}{2\triangle z}(x_1^2+y_1^2)}$ )의 convolution의 형태이다.
$U(x_2,y_2)=U(x_1,y_1)\star [\cfrac{e^{ik\triangle z}}{i\lambda \triangle z}\ e^{i\frac{k}{2\triangle z}(x_1^2+y_1^2)}]$
이것은 2개를 FT하여 곱하여 IFT

2. 연산자

Fresnel 회절 계산을 단순히 하기 위해 operator를 아래와 같이 적응할 수 있다. Nazarathy and Shamir

$\mathcal{Q}[c,\mathbf{r}]\ \{U(\mathbf{r})\}\equiv e^{i\frac{k}{2}c|\mathbf{r}|^2}\ U(\mathbf{r})$
$\mathcal{V}[b,\mathbf{r}]\ \{U(\mathbf{r})\}\equiv b\ U(b\mathbf{r})$
$\mathcal{F}[\mathbf{r},\mathbf{f}]\ \{U(\mathbf{r})\}\equiv \int\limits_{-\infty}^{\infty}\ U(\mathbf{r})\ e^{-i2\pi\mathbf{f\cdot r}}\ d\mathbf{r}$
$\mathcal{F}^{-1}[\mathbf{f},\mathbf{r}]\ \{U(\mathbf{f})\} \equiv\int\limits_{-\infty}^{\infty}\ U(\mathbf{r})\ e^{i2\pi\mathbf{f\cdot r}} d\mathbf{f}$
$\mathcal{R}[d. \mathbf{r}_1, \mathbf{r}_2]\ \{U(\mathbf{r}_1)\}\equiv \cfrac{1}{i\lambda d}\ \int\limits^{\infty}_{-\infty} U(\mathbf{r_1})\ e^{i\frac{k}{2d}|r_2-r_1|^2} d\mathbf{r}_1$

연산자의 parameter는 [∙]에 주어지고,
operand(연산 대상)는 {∙}에 주어진다.

$\mathcal{F}$ 연산자의 경우, (operand)연산 대상의 domain을 첫번째 parameter에 넣고, domain의 결과가 될 것은 두번째 parameter로 설정한다.

2차 위상 exponential 연산자의 경우

$\mathcal{Q}_2[d, \mathbf{r}]\ \{U(\mathbf{r})\}\equiv e^{i\pi^2\frac{2d}{k}|\mathbf{r}|^2}\ U(\mathbf{r})$
Nazarathy and Shamir가 정의한 연산자와 다음 관계를 가짐
$\mathcal{Q}_2[d,\mathbf{r}]=\mathcal{Q}[\cfrac{4\pi^2}{k^2}d,\mathbf{r}]$

3. Fresnel 적분 계산

$U(x_2, y_2)=\cfrac{e^{ik\triangle z}}{i\lambda\triangle z}\ e^{i\frac{k}{2\triangle z}(x^2_2+y_2^2)}\times \int\limits^{\infty}_{-\infty} \int\limits^{\infty}_{-\infty}\ U(x_1, y_1)\ e^{i \frac{k}{2\triangle z}(x_1^2+y_1^2)}\ e^{-i\frac{2\pi}{\lambda\triangle z}(x_2x_1+y_2y_1)}\ dx_1\ dy_1$
식으로 Fresnel 회절 적분을 구현하기 위해 2가지 방법을 소개
1. 가장 직관적인 방법으로 하나의 푸리에 변환으로 한 번 적분 계산한다(효율적).
2. Fresnel 적분을 2번 계산하여 2번째 FT 계산 비용에서는 grid spacing에 대한 유연함을 추가할 수 있다.

3.1 One-step propagation

위 식대로 $U(x_1,y_1)$ 과 어떻게 전파되는지 주어지면 observation-plane field인 $U(x_2,y_2)$ 를 직접적으로 계산할 수 있다.

$U(\mathbf{r}_2)=\mathcal{R}[\triangle z, \mathbf{r}_1, \mathbf{r}_2]\ \{U(\mathbf{r_1}) \}$
$=\mathcal{Q}[\cfrac{1}{\triangle z}, \mathbf{r}_2]\ \mathcal{V}[\cfrac{1}{\lambda \triangle z}, \mathbf{r}_2]\ \mathcal{F}\ [\mathbf{r}_1, \mathbf{f}_1] \mathcal{Q}\ [\cfrac{1}{\triangle z}, \mathbf{r}_1]\ \{U(\mathbf{r}_1)\}$

연산 순서는 오른쪽에서 왼쪽이다. 일반적으로, 이 operator들은 교환법칙이 성립하지 않음. 특정 조합만 가능.
observation field는 source field를 곱하고 quadratic phase $\mathcal{Q}$ , FT $\mathcal{F}$ , scaling[ $\mathcal{V}$ , 공간 주파수로부터 공간 좌표로 변환 $\mathbf{f}_1=\mathbf{r}_2/(\lambda \triangle z)$ ] 대입, 다른 quadratic phase $\mathcal{Q}$ 를 곱한다.

직관적인 설명으로 전파는 source와 observation 평면에 중심에 맞춰진 confocal sphere(두개의 구가 서로 공통 초점을 가질 때, 이러한 구)들 사이에 FT이다.
그 sphere들의 공통 곡률 반지름은 $\triangle z$ 다.

Fresnel 적분을 컴퓨터에서 계산하기 위해서, source-plane optical field인 $U(\mathbf{r_1})$ 의 샘플된 버전을 사용해야 한다.
source 평면의 spacing을 $\delta_1$ 이라고 할 때,
주파수 영역에서 spacing은 $\delta_{f1}=1/(N\delta_1)$ 이다.
따라서 observation 평면에서 spacing은
$\delta_2=\cfrac{\lambda\ \triangle z}{N\delta_1}$

3.1.1 코드 구현

함수 정의

import numpy as np
import matplotlib.pyplot as plt

def one_step_prop(Uin, wavelength, dl, distance):
    k = 2*np.pi/wavelength

    sc = np.arange(-N/2, N/2)*dl
    x1, y1 = np.meshgrid(sc,sc)
    oc = np.arange(-N/2, N/2) * wavelength * distance / (N*dl)
    x2, y2 = np.meshgrid(oc, oc)

    Uout = 1/(1j*wavelength*distance) * np.exp(1j*k/(2*distance) * (x2**2+y2**2)) * np.fft.fft2( Uin * np.exp(1j*k/(2*distance)*(x1**2+y1**2))) * dl **2
    
    return x2, y2, Uout

def rect2(t,T):
    return np.where(np.abs(t) < T/2, 1, 0)

실행

N = 1024  # number of grid points
L = 1e-2  # total size of the grid[m]
delta1 = L/N # grid spacing [m]
D = 2e-3     # diameter of the aperture [m]
wavelength = 1e-6 # optical wavelength[m]
k = 2*np.pi/wavelength

distance = 1 # propagation distance [m]

x = np.arange(-N/2, N/2)*delta1
x1, y1 = np.meshgrid(x,x)
aperture = rect2(x1,D)*rect2(y1,D)

x2, y2, Uout = one_step_prop(aperture, wavelength, delta1, distance)
Uout_shift = np.fft.fftshift(Uout)

plt.figure(figsize=(18,6))
plt.subplot(1,2,1)
plt.imshow(np.abs(aperture), cmap='gray', extent=(x1.min(),x1.max(), y1.min(),y1.max()))
plt.subplot(1,2,2)
plt.imshow(np.abs(Uout_shift), cmap='gray', extent=(x2.min(), x2.max(), y2.min(), y2.max()))
plt.show()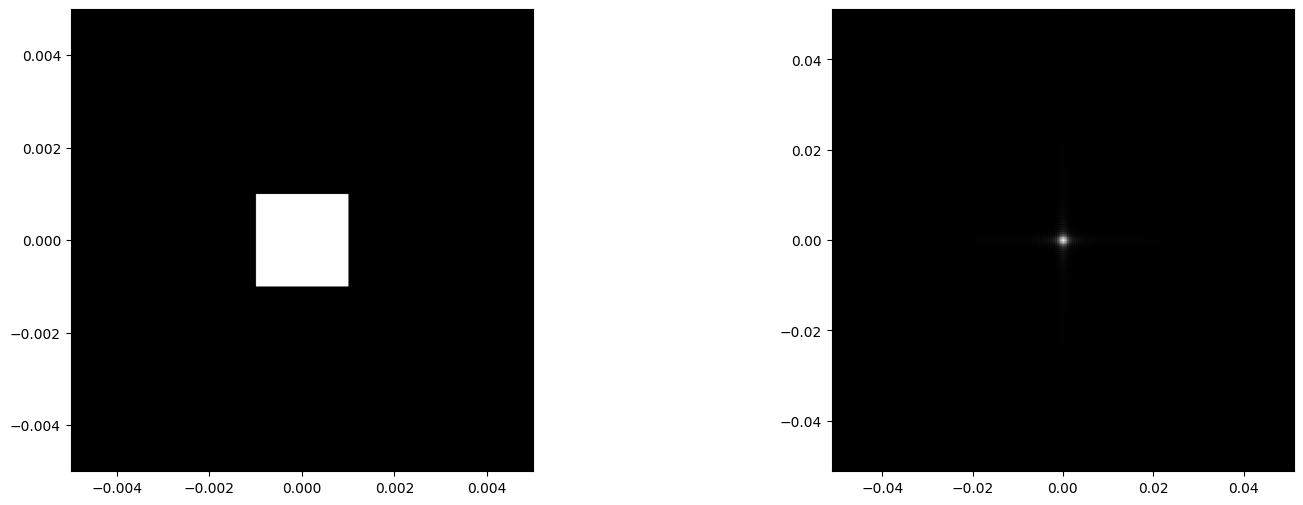

그래프 그리기

plt.figure(figsize=(16,6))
plt.subplot(1,2,1)
plt.xlim(-0.003,0.003)
plt.plot(x2[1], np.abs(Uout_shift[int(N/2)])**2, marker='x')

plt.subplot(1,2,2)
plt.xlim(-0.003,0.003)
plt.plot(x2[1], np.angle(Uout_shift[int(len(Uout_shift)/2)]), marker='x')
plt.show()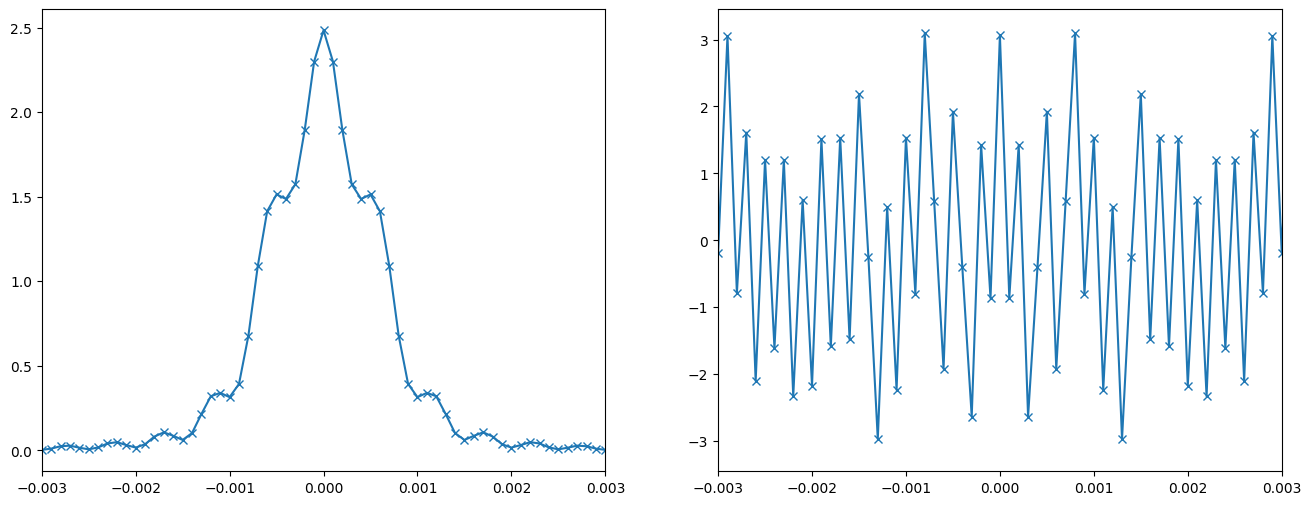

보다시피, 명백하게, observation grid에서 spacing을 조절할 수 없다.
$\delta_2=\cfrac{\lambda\ \triangle z}{N\delta_1}$
이미 observation plane에서는 grid spacing이 다음으로 고정된다.
만약 고정된 값 $\delta_2$ 가 observation 평면에서 sample하게 충분하지 않으면,
우리는 $N$ 을 늘려서 observation 평면을 더 세밀하게 샘플링할 수 있다.
하지만, $N$ 이 증가하는 것은 시뮬레이션 실행시간을 더욱 길게 하기 때문에 선호되지 않는다.

3.2 Two-Step Propagation

observation 평면 grid spacing( $\delta_2$ )를 선택하기 위해서, 새로운 scaling 인자인 $m=\cfrac{\delta_2}{\delta_1}$ 을 도입해야 한다.
one-step propagation에서는 $m$ 은 선택하는 자유가 없었다. $N$ 을 조절하는 것외에는

Coy,의 grid spacing 분석으로, Rydberg and Bengtsson은 grid를 선택함에 있어 더 유연한 알고리즘을 소개했다.
이 방법은, $U(x_1,y_1)$ 이 source 평면( $z_1$ )으로부터 중간 평면 $z_{1a}$ 까지 전파하고, 그 후 observation 평면( $z_2$ ) 평면까지 전파한다.
$z_{1a}$ 를 선택하기 위해 m(즉, $\delta_2$ )을 적절한 값으로 선택해야 한다.

source 평면: $z=z_1$ ( $\mathbf{r}_1$ 좌표계)
observation 평면: $z=z_2$ ( $\mathbf{r}_2$ 좌표계)
$\triangle z=z_2-z_1$
scaling parameter: $m=\cfrac{\delta_2}{\delta_1}$
intermediate 평면: $z=z_{1a}$ ( $\mathbf{r}_{1a}$ 좌표계)
첫 번째 전파 거리: $\triangle z_{1}=z_{1a}-z_{1}$
두 번째 전파 거리: $\triangle z_{2}=z_{2}-z_{1a}$

$\triangle z_{1}$ , $\triangle z_{2}$ 는 아래 그림처럼 2가지 방식으로 표현될 수 있다.

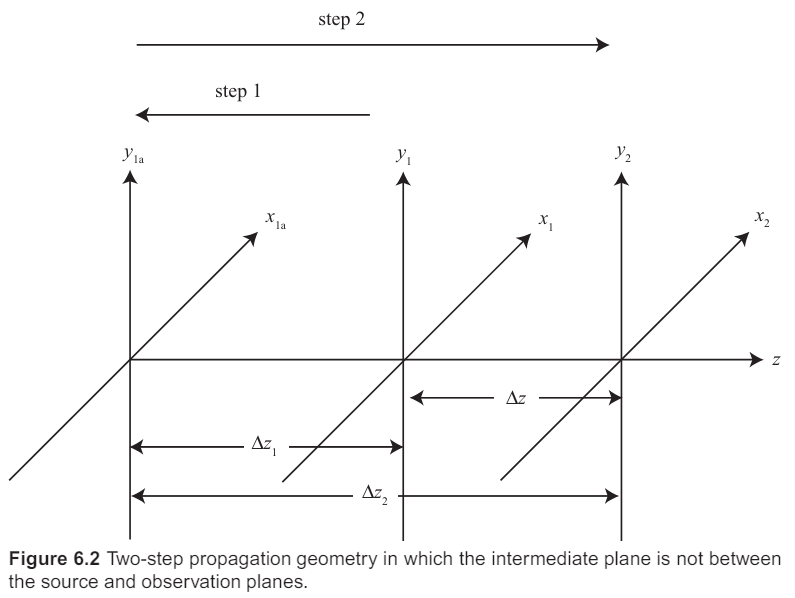
3.2.1 intermediate - source - observation

$\triangle z_1^-$ , $\triangle z_2^-$ 로 정의

3.2.2 source - intermediate - observation

$\triangle z_1^+$ , $\triangle z_2^+$ 로 정의

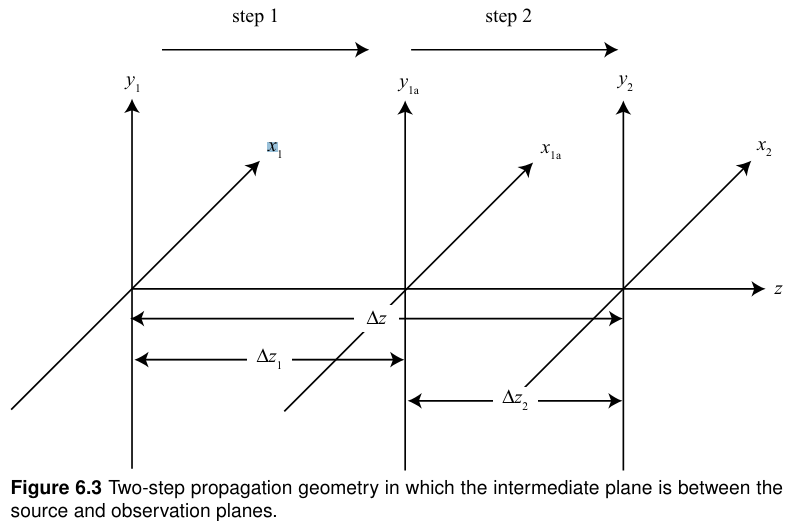
Fresnel 적분 전파에서 two step은
$U(\mathbf{r_2})=\mathcal{R}[\triangle z_2, \mathbf{r}_{1a}, \mathbf{r}_{2}]\ \mathcal{R}[\triangle z_1, \mathbf{r}_{1}, \mathbf{r}_{1a}]\ \{ U(\mathbf{r}_1) \}$
$=\mathcal{Q[\cfrac{1}{\triangle z_2}, \mathbf{r_2}]}\ \mathcal{V}[\cfrac{1}{\lambda \triangle z_2}]\ \mathcal{F}[\mathbf{r}_2, \mathbf{f}_{1a}]\ \mathcal{Q}[\cfrac{1}{\triangle z_2}, \mathbf{r_{1a}}] \times \mathcal{Q[\cfrac{1}{\triangle z_1}, \mathbf{r_{1a}}]}\ \mathcal{V}[\cfrac{1}{\lambda \triangle z_1}]\ \mathcal{F}[\mathbf{r}_1, \mathbf{f}_{1}]\ \mathcal{Q}[\cfrac{1}{\triangle z_1}, \mathbf{r_{1}}]\ \{U(\mathbf{r}_1) \}$

intermediate 평면에서 spacing $\delta_{1a}$ 와 observation 평면에서 spacing $\delta_{2}$ 조사하면, 다음 값을 구할 수 있다.

$\delta_{1a}=\cfrac{\lambda|\triangle z_1|}{N\delta_1}$ , with $\triangle z_1=z_{1a}-z_1$

$\delta_2=\cfrac{\lambda|\triangle z_2|}{N\delta_{1a}}=|\cfrac{\triangle z_2}{\triangle z_1}| \delta_1=m\delta_1$

scaling parameter 정의는 m= $\cfrac{\delta_2}{\delta_1}$

따라서, m의 선택은 intermediate 평면의 위치에 따라 정의된다.
즉, $m=|\cfrac{z_2-z_{1a}}{z_{1a}-z_1}|=|\cfrac{\triangle z_2}{\triangle z_1}|$

즉 intermidate 평면의 위치 $z_{1a}$ 값에 따라,
$\triangle z_1=z_{1a}-z_1=\triangle z (\cfrac{1}{1±m})$

$\triangle z=\triangle z_1+ \triangle z_2$
$\triangle z=\triangle z_1±m\triangle z_1$
$\triangle z=\triangle z_1(1±m)$

$\triangle z_{1a}=z_1+\triangle z(\cfrac{1}{1±m})$
$\triangle z_{2} = z_2-z_{1a}=\triangle z(\cfrac{±m}{1±m})$
$z_{1a}=z_2-\triangle z(\cfrac{±m}{1±m})$
$z_{1a}=z_2+\triangle z(\cfrac{∓m}{1±m})$

3.2.3 2-step 코드 구현

함수 선언

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import fresnel


def two_step_prop(Uin, wavelength, d1, d2, distance):
    k = 2*np.pi/wavelength
    sc = np.arange(-N/2, N/2)*d1
    x1, y1 = np.meshgrid(sc,sc);

    # magnification
    m = d2/d1
    # intermediate plane
    dz1 = distance / (1-m) # Propagation Distance
    d1a = wavelength * abs(dz1) / (N*d1) # coordinates
    ic = np.arange(-N/2, N/2)*d1a
    x1a, y1a = np.meshgrid(ic, ic)
    Uitm = 1 / (1j*wavelength*dz1) * np.exp(1j*k/(2*dz1)*(x1a**2+y1a**2)) * np.fft.fft2(Uin*np.exp(1j*k/(2*dz1)*(x1**2+y1**2)))*d1*d1
    
    
    # observation plane
    dz2 = distance - dz1  # Propagation Distance
    # coordinates
    oc = np.arange(-N/2, N/2)*d2
    x2, y2 = np.meshgrid(oc, oc)

    # evaluate the Fresnel diffraction integral
    Uout = 1/ (1j*wavelength*dz2)*np.exp(1j*k/ (2*dz2) * (x2**2+y2**2)) * np.fft.fft2(Uitm*np.exp(1j*k/(2*dz2)*(x1a**2+y1a**2)))*d1a*d1a

    return x2, y2, Uout

def rect(x, a):
    tmp = np.where(np.abs(x) < a/2, 1, 0)
    return np.where(np.abs(tmp)==a/2, 0.5, tmp) 

def fresnel_prop_square_ap(x2, y2, D1, wavelength, distance):
    N_F = (D1/2)**2 / (wavelength * distance) # Fresnel number

    # substitutions
    bigX = x2 / np.sqrt(wavelength*distance)
    bigY = y2 / np.sqrt(wavelength*distance)
    alpha1 = -np.sqrt(2)*(np.sqrt(N_F)+bigX)
    alpha2 = np.sqrt(2)*(np.sqrt(N_F) -bigX)
    beta1  = -np.sqrt(2)*(np.sqrt(N_F)+bigY)
    beta2  = np.sqrt(2)*(np.sqrt(N_F)-bigY)
    # Fresnel sine and cosine integrals
    ca1, sa1 = fresnel(alpha1);
    ca2, sa2 = fresnel(alpha2);
    cb1, sb1 = fresnel(beta1);
    cb2, sb2 = fresnel(beta2);
    # observation-plane field
    U = 1/(2*1j)*((ca2-ca1)+1j*(sa2-sa1))*((cb2-cb1)+1j*(sb2-sb1))
    
    return U

Propagation 및 2D 시각화

N=1024  # number of grid points per side
L=1e-2  # total size of the grid[m]
delta1 = L/N # grid spacing [m]
D = 2e-3 # diameter of the aperture [m]
wavelength = 1e-6 # optical wavelength [m]
k = 2*np.pi / wavelength
distance = 1 # propagation distance [m]

sc = np.arange(-N/2, N/2)*delta1
x1, y1 = np.meshgrid(sc,sc)
aperture = rect(x1,D)*rect(y1,D)

delta2 = wavelength * distance / (N*delta1)
x2, y2, Uout = two_step_prop(ap, wavelength, delta1, delta2, distance)

# analytic result for y2=0 slice
Uout_an = fresnel_prop_square_ap(x2[int(N/2)+1], 0, D, wavelength, distance)
Uout_an2 = fresnel_prop_square_ap(x2, y2, D, wavelength, distance)

Uout_shift = np.fft.fftshift(Uout)

plt.figure(figsize=(18,4))
plt.subplot(1,3,1)
plt.imshow(np.abs(aperture), cmap='gray', extent=(x1.min(),x1.max(), y1.min(),y1.max()))
plt.subplot(1,3,2)
plt.imshow(np.abs(Uout_shift), cmap='gray', extent=(x2.min(), x2.max(), y2.min(), y2.max()))
plt.subplot(1,3,3)
plt.imshow(np.abs(Uout_an2), cmap='gray', extent=(x2.min(), x2.max(), y2.min(), y2.max()))
plt.show()

그래프 시각화

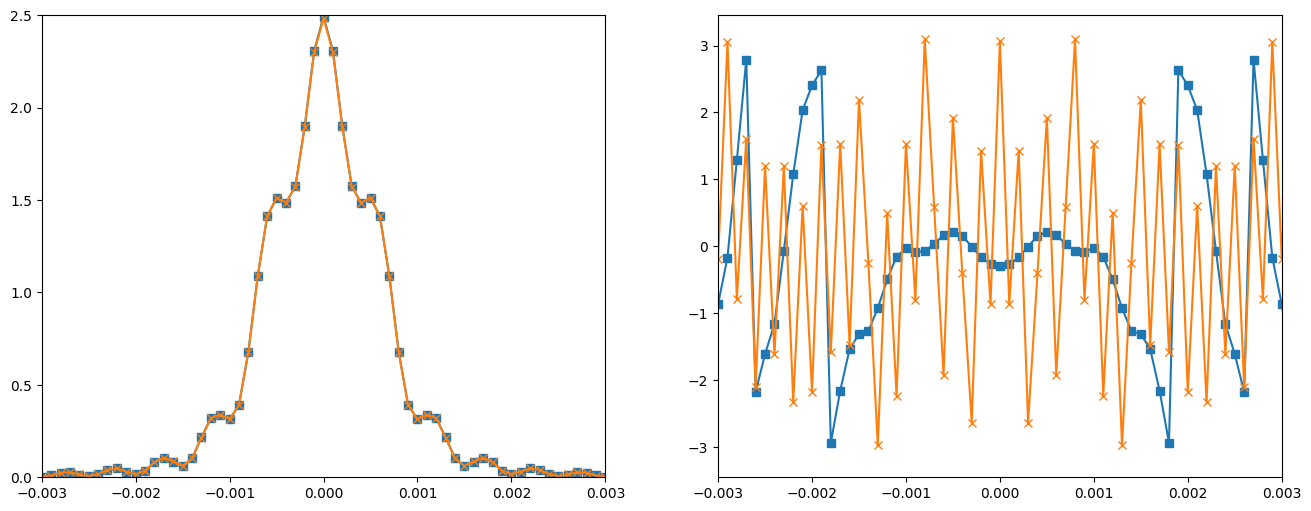
plt.figure(figsize=(16,6))
plt.subplot(1,2,1)
plt.xlim(-0.003,0.003)
plt.ylim(0,2.5)
plt.plot(x2[1], np.abs(Uout_an**2), marker='s')
plt.plot(x2[1], np.abs(Uout_shift[int(N/2)])**2, marker='x')

plt.subplot(1,2,2)
plt.xlim(-0.003,0.003)
plt.plot(x2[1], np.angle(Uout_an), marker='s')
plt.plot(x2[1], np.angle(Uout_shift[int(len(Uout_shift)/2)]), marker='x')
plt.show()