이번에는 near-field diffraction(근거리 회절)애 대해 다루고자 한다.
이는 단색(monochromatic) 파동에 대한 paraixal approximation(축 근사)를 사용하는 Fresnel 회절 적분에 의해 결정된다.

$U(x_2,y_2)=\cfrac{e^{jk\triangle z}}{j\lambda \triangle z}e^{j\frac{k}{2\triangle z}(x_2^2+y_2^2)}\ \int\limits^{\infty}_{-\infty}\int\limits^{\infty}_{-\infty}\ U(x_1,y_1) \times\ e^{j\frac{k}{2\triangle z}(x_1^2+y_1^2)} e^{-j\frac{2\pi}{\lambda \triangle z}(x_2x_1+y_2y_1)}dx_1dy_1$

Fraunhofer 근사인 $\triangle z > \cfrac{2D^2}{\lambda}$를 적용하면 위 식에서 quadratic phase exponential(2차 phase 항)이 제거된다. 결과적으로 Faunhofer 회절 적분이 된다.

하지만 근거리 회절의 경우에는 위 근사가 적용되지 않는다.

완벽한 구형(근축 근사에서) 및 얇은 렌즈에 의해 생기는 위상 지연 다음과 같이 주어진다.

• $x, y$: exit-pupil(빛이 렌즈를 통과한 후 모이는 평면)렌즈 평면에서 좌표
• $f_l$은 초점거리다.

$\phi(x,y)=\cfrac{k}{2f_l}(x^2+y^2)$

투명한 평면 물체가 3가지 중 한 위치에 놓일 수 있다.
1. 렌즈에 닿은 상태(앞에)
2. 렌즈 앞에
3. 렌즈 뒤에

이 물체는 수직 입사하고 무한한 범위와 균일한 진폭을 갖는 plane wave에 의해 조명된다.
물체를 통과하는 빛을 렌즈의 후초점 평면으로 전파하는데 $U(x_2,y_2)$ 식을 사용할 수 있다.

결과적으로 phase term($\phi(x,y)$)는 Fresnel 회절 적분 안에서 $U(x_1,y_1)$의 부분이 된다. 이는 더 간단화할 수 있다.

1. 물체가 렌즈 앞에 닿은 상태

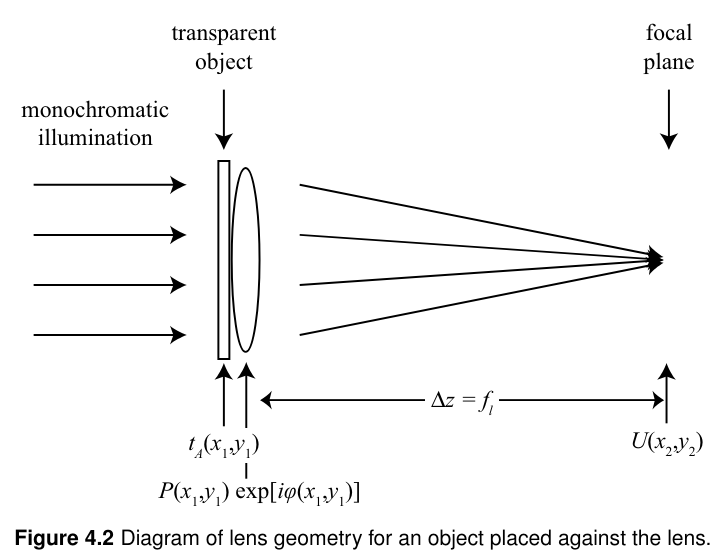
렌즈 바로 뒤 plane에서 optical field를 다음과 같이 정의할 수 있다.

• $t_A(x_1,y_1)$: 물체의 통과하는 빛의 비율(aperture transmittance)
• $P(x_1,y_1)$: lens에 의한 apodization을 설명하는 실수 함수
  - 광학 시스템의 입력 강도 프로파일을 의도적으로 변경하는 데 사용
  • transmission profile that approaches zero at the edges.)

$U(x_1,y_1) = t_A(x_1, y_1)\ P(x_1,y_1)e^{-j\frac{k}{2f_l}(x^2_1+y_1^2)}$

focal plane에서니깐 $\triangle z=f_l$

$U(x_1,y_1)$을 Fresnel 회절 적분에 대입하면,

$U(x_2,y_2)=\cfrac{e^{jk\ f_l}}{j\lambda\ f_l}e^{j\frac{k}{2\ f_l}(x_2^2+y_2^2)}\ \int\limits^{\infty}_{-\infty}\int\limits^{\infty}_{-\infty}\ t_A(x_1,y_1) \times\ P(x_1,y_1)\ e^{j\frac{k}{2f_l}(x_1^2+y_1^2)}e^{-j\frac{2\pi}{2 f_l}(x_1^2+y_1^2)}\ e^{-j\frac{2\pi}{\lambda f_l}(x_2x_1+y_2y_1)}dx_1dy_1$

$=\cfrac{e^{jk\ f_l}}{j\lambda\ f_l}e^{j\frac{k}{2\ f_l}(x_2^2+y_2^2)}\ \int\limits^{\infty}_{-\infty}\int\limits^{\infty}_{-\infty}\ t_A(x_1,y_1) \times\ P(x_1,y_1)\ e^{-j\frac{2\pi}{\lambda f_l}(x_2x_1+y_2y_1)}dx_1dy_1$

위 식을 Fourier Transform의 형태로 변환하면
$U(x_2,y_2)=\cfrac{e^{jk\ f_l}}{j\lambda\ f_l}e^{j\frac{k}{2\ f_l}(x_2^2+y_2^2)}\ \mathcal{F}\{ t_A(x_1,y_1) P(x_1,y_1)\}|_{f_x=\frac{x_2}{\lambda f_l}, f_y=\frac{y_2}{\lambda f_l}}$

수렴 렌즈에 닿게 놓인 물체의 경우, 물체 평면에서 초점 평면으로의 전이를 아래 lens_against_ft 함수로 제공

2. 물체가 렌즈 전에 있는 경우

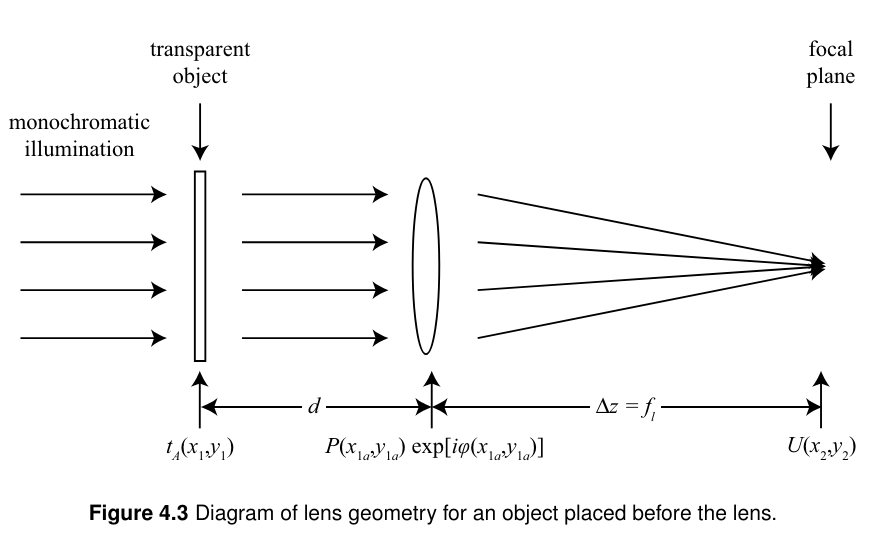
렌즈 뒤 $d$만큼 떨어진 위치에 놓인 일반적인 상황에서 빛이 초점 평면으로 전파하면,
렌즈 aperture에 의해 물체의 vignetting(비네팅)을 고려하기 위해 조리개 pupil 함수인 $P(∙)$의 인자가 shift된다.

• Vignetting: 광학 시스템에서 빛이 모이는 곳에 도달하는 데 필요한 경로가 차단되어 광학 성능이 저하되는 현상

focal plane에서 각 점은 광축 상의 점에서 가장 작은 vignetting을 경험한다.

$U(x_2,y_2)=\cfrac{e^{jk\ f_l}}{j\lambda\ f_l}e^{j\frac{k}{2\ f_l}(1-\frac{d}{f_l})(x_2^2+y_2^2)}\ \int\limits^{\infty}_{-\infty}\int\limits^{\infty}_{-\infty}\ t_A(x_1,y_1) \times\ P(x_1+\cfrac{d}{f_l}x_2,\ y_1+\cfrac{d}{f_l}y_2)\ e^{-j\frac{2\pi}{\lambda f_l}(x_2x_1+y_2y_1)}dx_1dy_1$

결국 FT로 표현하면,
$U(x_2,y_2)=\cfrac{e^{jk\ f_l}}{j\lambda\ f_l}e^{j\frac{k}{2\ f_l}(1-\frac{d}{f_l})(x_2^2+y_2^2)}\ \times \mathcal{F}\{ t_A(x_1,y_1) P(x_1+\cfrac{d}{f_l}x_2,\ y_1+\cfrac{d}ㄴ{f_l}y_2)\}|_{f_x=\frac{x_2}{\lambda f_l}, f_y=\frac{y_2}{\lambda f_l}}$

여기서 흥미로운 case가 있는데, 물체를 lens에 바로 닿는 d=0이면 #1 경우와 같은 해가 된다.
두번째는 $d=f_1$ 에 물체가 focal plane에 놓이는 경우,
밖의 phase factor가 1이 된다. 정확하게 푸리에 변환만 가지고 관계식이 된다.

3. 물체가 렌즈 후에 있는 경우

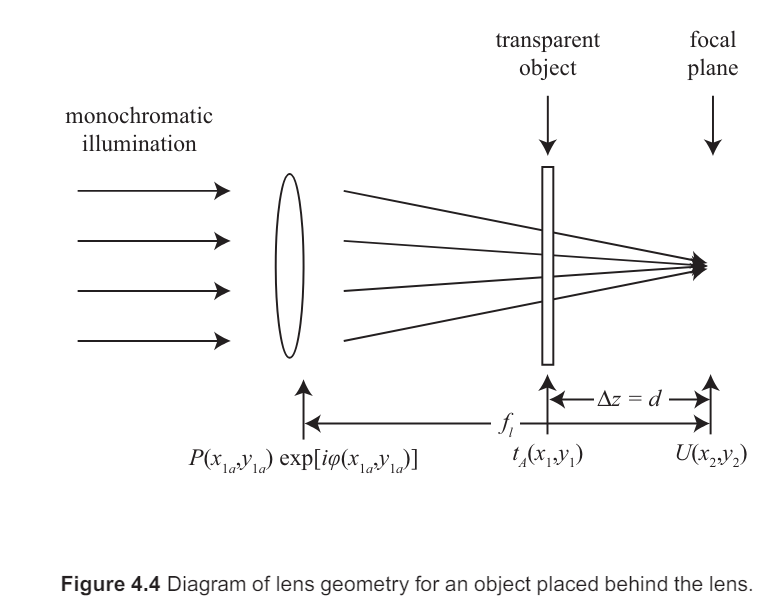
위 그림과 같이 focal plane으로부터 d만큼 lens 후에 물체가 있는 경우 optical field $U_s(x_1,y_1)$은 물체 바로 전에서 수렴하는 구면파로 다음과 같이 주어진다.