광 전파에서 대기 turbulence 효과를 분석적 결과로 도출하는 것은 간단한 통계적 모델을 가정할 때 가능하다. 하지만, 적응 광학 시스템을 사용하여 더 복잡한 시나리오를 고려하는 것을 원하는 경우, 보통 보정된 optical field의 통계는 closed form에서 계산될 수 없다.
수식 단순화를 위해, 흔한 테크닉은 turbulence를 유한한 이산적인 layer로 다루는 것이다. 이 분석적 계산, simulation, turbulence를 실험실에서 모방할 때 흔한 방법이다.
layered model은 해당 extended 매질의 굴절률 spectrum과 scintillation 특성에 맞다면 유용하다. 각 layer는 더욱 큰 두께의 turbulent 부피를 표현하는 얇은 phase screen 단일 진폭이다. 만약 phase screen의 두께가 screen 향하는 전파 거리보다 훨씬 작다면, phase screen은 얇게 고려된다. phase screen은 대기 phase perturbation(작은 변화)의 하나 구현이고 T[zi,zi+1]=exp[−ϕ(ri+1)] 굴절 연산자를 구현할 수 있다. 이것은 대기 전파를 시뮬레이션 하기 위해 대기 phase screen을 split-step beam 전파 방법을 어떻게 통합하는지 보여준다.
1. split-step beam propagation
진공이 아닌 매질에 대한 전파를 시뮬레이션은 split-step beam propagation method를 통해 달성할 수 있는데, 많은 material 종류들에서 유용하다. (불균등하고, 이방성, 비선형적)
여기서는 대기에 국한하여 선형적이고, 등방적인 물질인데 불균등한 굴절률(n)을 n=n(x,y,z)에 대해서 논한다. δn=n−1이 작을 때,
i+1번째 평면에서 보이즌 field는
U(ri+1)≃R[2△zi,ri,r~i+1] T[zi,zi+1] R[2△zi,ri,r~i+1] {U(ri)}
T[zi,zi+1]은 phase의 축적을 표현하는 연산자이며, r~i+1은 i, i+1 평면 상이 중간 평면의 좌표이다.
T[zi,zi+1]=exp[−iϕ(ri+1)]
축적된 phase는 ϕ(ri)=k∫zizi+1δn(ri)dz, 즉 굴절률 차이만큼의 누적의 파수 k배이다.
매질을 통해 통한 전파를 2가지 효과로 분리할 수 있다.
- 회절(diffraction)
자유공간의 회절은 연산자 R
- 굴절(refraction)
굴절은 연산자 T
이 방법은 atmospheric turbulence를 통한 전파를 시뮬레이션하는데 자주 사용된다. 실제로, 광학 실험실에서 turbulence를 통한 propgation을 emulate(모사)할 때 사용하기도 한다.
빛과 매질 사이 상호작용이 있는 것에 대해 partial vaccum propagation을 대체 방법이다.
vaccum propgation 알고리즘을 살짝 고쳐 아래처럼 표현한다. interaction이 있는 평면 n개와 n-1개의 전파가 있을 때, vaccum 상황은 각 step에서 T=1일 때고, turbulence가 있는 경우 어떻게 T 구현을 생성할지가 중요하다.
U(rn)=Q[mn−1 △zn−1mn−1−1,rn]
×i=1∏n−1{T[zi,zi+1]F−1[fi,miri+1] Q2[−mi△zi,fi] F[ri,fi]mi1}
×{Q[△z11−m1,r1] T[z1,z2] U(r1)}
- Q[c,r]{U(r)}≡ei2kc∣r∣2U(r)
- Q2[d,r]{U(r)}≡eiπ2k2d∣r∣2U(r)
- F[r,f]{U(r)}≡−∞∫∞U(r)e−i2πf⋅rdr
def ang_spec_multi_prop(Uin, wavelength, delta1, deltan, z, t):
N = Uin.shape[0]
n_1d = np.arange(-N/2,N/2)
nx, ny = np.meshgrid(n_1d, n_1d)
k = 2*np.pi/wavelength
nsq = nx**2+ny**2
w = 0.47*N
sg = np.exp(-nsq**8/w**16)
z = np.insert(z, 0, 0)
n = len(z)
Delta_z = z[1:n]-z[0:n-1]
alpha = z / z[n-1]
delta = (1-alpha) * delta1 + alpha * deltan
m = delta[1:n] / delta[0:n-1]
print(m)
x1 = nx * delta[0]
y1 = ny * delta[0]
rlsq = x1**2+y1**2
-
Q1=ei2k△z11−m1∗(x12+y12)∗Uin(x1,y1)
-
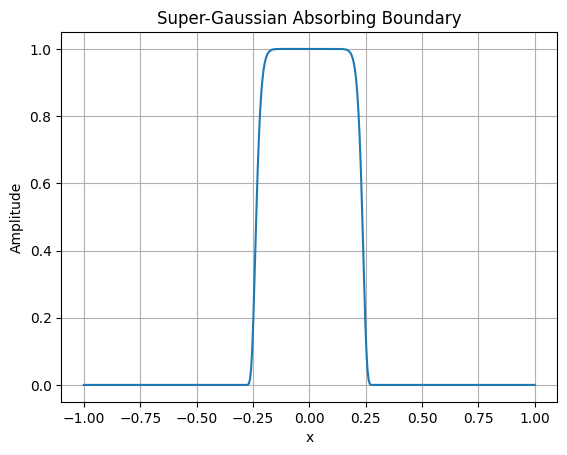
T(x)=e−(x/σ)2n
- n=8
- σ=0.47∗N∗d1
sg = np.exp(-(x1/(0.47*N*d1))**16) * np.exp(-(y1/(0.47*N*d1))**16)
Q1 = np.exp(1j*k/2*(1-m[0])/Delta_z[0]*rlsq)
Uin = Uin * Q1 * t[0,:,:]
- Q2=eiπ2k−2△zi/mi∣fx2+fy2∣
- 1/mi→F→Q2→F−1→T
for idx in range(0, n-1):
delta_f = 1 / (N*delta[idx])
fX = nx * delta_f
fY = ny * delta_f
fsq = fX**2+fY**2
dZ = Delta_z[idx]
Q2 = np.exp(-1j*np.pi**2 *2*dZ/(m[idx]*k)*fsq)
Uin = sg * t[idx+1,:,:] * np.fft.ifft2(np.fft.fftshift(Q2)*np.fft.fft2(Uin/m[idx], norm='ortho'), norm='ortho')
- Uout=ei2kmn−1△zn−1mn−1−1∗(xn2+yn2)∗Uin(xn,yn)
Q[mn−1 △zn−1mn−1−1,rn]
xn = nx*delta[n-1]
yn = ny*delta[n-1]
rnsq = xn**2+yn**2
Q3 = np.exp(1j*k/2*(m[n-2]-1)/(m[n-2]*dZ) *rnsq)
Uout = Q3 * Uin
return xn, yn, Uout
2. Theory
이론적으로 대기 phase screen을 나타내기 위해, 유효 구조 상수 Cni2의 항으로 turbulence profile을 나타낸다.
- zi:전파 거리
- △zi: i번째 phase screen에 표현되는 확장된 turbulence의 판 두께
Cni2 값은 연속 모델의 모델의 중요한 통계적 특성(평균, 분산, 갯수, low order moments)를 layer model에 맞추기 위해 선택된다.
0∫△ziCn2(z′)(z′)mdz′=i=1∑nCni2zim△zi
- n: 사용되는 phase screen 갯수 0≤m≤7
이러한 방법으로 layered 모델의 r0,θ0,σχ2이 원래의 turbulence의 매개변수와 맞춘다.
- layered turbulence model을 위한 대기 parameter들은 discrete-sum 버전을 사용해 계산된다.
- r0,pw=[0.423k20∫△zCn2(z)dz]−3/5
r0,pw=(0.423k2i∑Cni2△zi)−3/5
- r0,sw=[0.423k20∫△zCn2(z)(△zz)5/3dz]−3/5
r0,sw=[0.423k2i=1∑nCni2(△zzi)5/3△zi]−3/5
- σχ,pw2=0.563k7/6△z5/60∫△zCn2(z)(1−△zz)5/6dz
σχ,pw2=0.563k7/6△z5/6i=1∑nCni2(1−△zzi)5/6△zi
- σχ,sw2=0.563k7/60∫△zCn2(z)z5/6(1−△zz)5/6dz
σχ,sw2=0.563k7/6△z5/6i=1∑nCni2(△zzi)5/6(1−△zzi)5/6△zi
r0,pw=(0.423k2i∑Cni2△zi)−3/5을 이용하여, i번째 layer는 유효 coherence diameter r0i를 다음과 같이 표현하여 더 간단히 표현하면
r0i=[0.423k2Cni2△zi]−3/5
- r0,pw=(i=1∑nr0i−5/3)−3/5
- r0,sw=(i=1∑nr0i−5/3(△zzi)5/3)−3/5
- σχ,pw2=1.33k−5/6△z5/6i=1∑nr0i−5/3(1−△zzi)5/6
- σχ,sw2=1.33k−5/6△z5/6i=1∑nr0i−5/3(△zzi)5/6(1−△zzi)5/6
요구된 atmospheric 조건 set(r0,sw,σχ,sw2)이 주어지면, 예로 이 방정식들은 경로를 따른 위치와 phase screen 특성을 결정하는데 사용할 수 있다.
5~10 개의 보통 phase screen 수를 사용하면 10~20개의 모르는(각 screen 마다 r0,zi) 변수가 있다. 그래서 2개의 방정식으로 시스템을 결정할 수 없다.
partial-propagation planes의 균일한 spacing은 일관성을 유지할 수 있어 이러한 방법으로 phase screen 위치를 고정하여 향상시킬 수 해결할 수 있다. 각 partial-rpopagation plane에서 phase screen을 놓는 것을 선택한 다음 방정식을 단순화하는 αi=△zzi을 이용.
예로 5개의 screen이면,
[r0,sw−5/31.33σχ,sw2(△zk)5/6]=[00α25/3α25/6(1−α2)5/6α35/3α35/6(1−α3)5/6α45/3α45/6(1−α4)5/6α55/3α55/6(1−α5)5/6]⎣⎢⎢⎢⎢⎢⎢⎡r01−5/3r02−5/3r03−5/3r04−5/3r05−5/3⎦⎥⎥⎥⎥⎥⎥⎤
위 방법으로 왼쪽 항이 r0,sw,σχ,sw2가 결정된다.
- λ,△z,Cn2(z) 모델이 주어지면, 우리는 simulation을 위해 요구되는 atmospheric 매개변수를 계산한다.
- 위 행렬식과 같이, 적절한 시스템의 방정식을 풀어서, phase screen의 r0 값을 구한다.
- 이 접근 방식의 어려움은 r0 벡터에서 -5/3 승수가 있다는 점이다. r0 벡터에서 음수 항목은 물리적으로 불가능하므로, 해결된 r0 벡터의 값은 양수로 제한되어야 한다.
몇 개의 phase screen을 시뮬레이션하기 위한 r0 계산하기 위한 constrained optmization의 사용을 볼 수 있다.

