Fresnel propagation의 sampling 제약 조건은 엄격하다. 특히, angular-spectrum 방법은 짧은 거리 전파에 가장 적합하다. 주요 문제는 aliasing으로 인해 발생하는 wrap-around이다. 이러한 효과를 완화하기 위해 몇 가지 접근법이 제안되었다. 대부분의 접근법은 optical field를 공간적으로 감쇠시키고 필터링하는 데 중점을 둔다. 예를 들어, Johnston and Lane은 free-space transfer 함수가 필터링되고 grid size가 filter의 대역폭에 기반하여 설정하는 기술을 설명한다. 이 단계 후, 마찬가지로 2차 phase 인자의 aliasing을 피하기 위해 sample interval을 설정한다.

Johnston and Lane의 공간 필터 대역폭 선택은 효과적이지만 특정 wrap-around 효과와는 다소 간접적으로 관련되어 있다. 이 책은 보다 직접적인 접근법을 다룹니다.
고정된 $D_1$, $δ_1$, $D_2$ 및 $δ_2$에 대해 7장에 나온 constraint1, 3, 4를 만족시켜야 한다. 일반적으로 $∆z$도 고정되어 있으며, 이는 시뮬레이션하고자 하는 기하학적 요소의 일부이다. 종종 유일한 자유로운 parameter는 $N$이며, $∆z$가 클 경우 제약조건들은 큰 $N$을 요구한다. 때때로 $N > 4096$과 같이 필요한 $N$이 지나치게 커질 때가 있다. 보통 문제의 원인은 constraint4인데, 이는 고정된 propagation-geometry과는 관계없이 geometry method에만 의존한다. constraint 4가 만족되면, $N, δ_1, δ_2, λ$를 고정한 채로 $∆z$를 줄이면 계속 만족된다.

따라서, 이 장에서는 angular-spectrum 방법을 사용하여 constraint 4를 크게 완화시키는 multiple partial propagation을 개발한다. propagation 알고리즘을 설명하기 위해 먼저 8.2절에서 2개의 partial propagation를 시작으로, 8.3절에서 n-1개의 partial propagation(즉, n개의 평면)로 일반화한다.

처음에는 이것이 좋은 해결책처럼 들릴 수 있지만, multiple partial propagtion들은 수학적으로 single full propagation와 동등하다. 추가적인 partial propagation은 실행 시간이 더 오래 걸릴 뿐이다. 우리가 완화하고자 하는 주요 어려움은 aliasing으로 인한 wrap-around이다. $∆z$가 증가함에 따라 $H(\mathbf{f}_1)=e^{ik\triangle z}e^{-i\pi\lambda \triangle z(f^2_{x1}+f^2_{y1})}$ free space transfer 함수의 변동이 점점 더 급해진다. 따라서 wrap-around 효과가 grid의 edge에서 중심으로 스며든다. partial propagation을 통해, 우리는 grid edge에서 field를 감쇠시켜 경로를 따라 wrap-around를 억제할 수 있다. 이 방법은 시뮬레이션 방법의 사용 가능한 조건 범위를 늘리거나 실행에 비용이 많이 드는 grid size를 줄이는 데 도움이 된다.
대부분의 경우 시뮬레이션의 실행 시간이 줄어든다.

wrap-around란?
주로 FFT와 같은 주기적인 경계 조건을 사용하는 DFT에서 발생한다. 이는 신호가 grid의 edge를 넘어갈 때 발생하는데, 이 경우 신호의 한쪽 끝이 다른 쪽 끝과 연결되어 원래 신호의 모양을 왜곡시킨다. 즉, 신호가 grid edge를 넘어가면서 신호가 잘못 연결되고 왜곡되는 현상

---

1. Absorbing Boundaries

edge에서 field를 감쇠를 시키면, grid의 범위를 넘어 퍼지는 에너지를 흡수하는 효과를 갖는다.
이 동작은 단순히 각 partial-propagation 평면에서 감쇠 인자를 field에 곱해주면 된다.
이것은 data windowing 개념과 유사하지만, grid의 중앙 영역의 빛을 변경하지 않도록 주의해야 한다.
이러한 이유로 attenuation factor는 중심에서는 1에 가깝고 edge에서는 0에 가깝다. 흔한 data windows인 Hamming and Barlett winodws의 경우 이 목적에 맞지 않다.

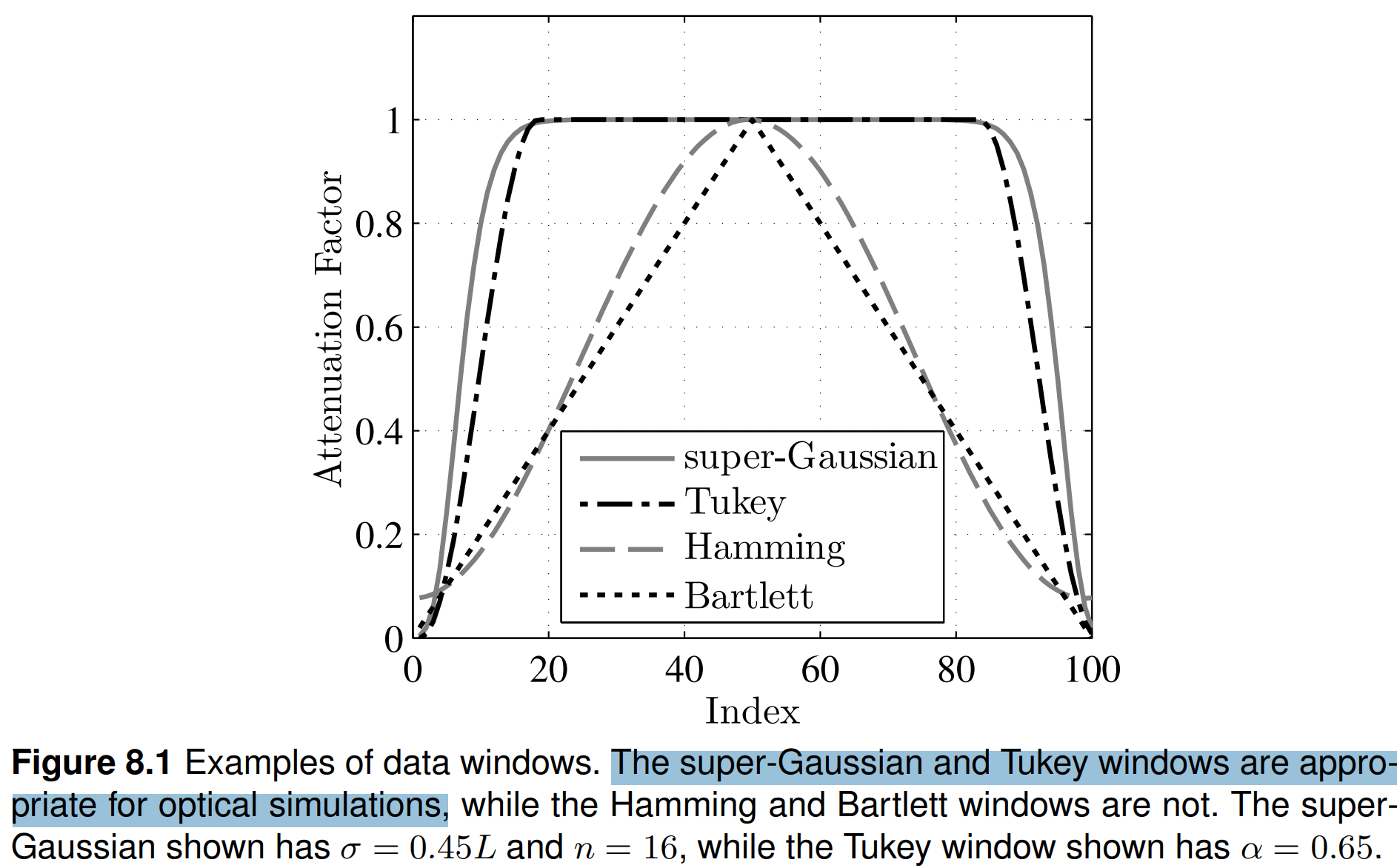
잘 맞는 attenuation factor로는

1. super Gaussian 함수는 $n>2$일 때 다음과 같이 정의된다.
   $g_{sg}(x,y)=\exp[-(\frac{r}{\sigma})^n], n >2$

2. Tukey(or cosine-taper) window는 다음과 같이 정의,
   $\alpha$: tapered(점점가늘어지는) 영역의 너비 인자 $0\le\alpha\le1$
   $g_{ct}(x,y)=\begin{cases} 1 & \text{if } r\ge \frac{\alpha L}{2} \\ \frac{1}{2}\{1+\cos[\pi\frac{r/L-\alpha N/2}{(1-\alpha N/2)}]\} & \text{if } \frac{\alpha N}{2} \le \frac{r}{L}\le \frac{N}{2} \end{cases}$

큰 $\alpha$ 값들은 중심에서 넓게 감쇠되지 않은 영역을 나타내고, edge에서는 점점가늘어지는 것을 보인다.

• Flatte, et al은 turbulent 전파 연구에서 평면파를 모델링하는데 $n=8$인 super-Gaussian을 사용했다.

• Rubio는 전파 경로 전체에서 흡수 경계로 동일한 유형의 super-Gaussian을 채택했다.
  - 발산하는 구면파로부터 energy를 포함하기 위해 사용됐다.

• Frehlich는 대기 phase screen 형성 연구에 Tukey window가 사용되었다.

• Martin and Flatte는 대기 turbulence를 통한 전파 시뮬레이션에서 Gaussian 소멸(extinction) 계수로 사용했다.

  이를 하기 위해, 그들은 random 대기 phase screen에 deterministic(특정한 규칙이나 수식에 의해 결정되고 예측가능한) 허수부를 더했고, 따라서 grid의 edge에서 Gaussian 인자만큼 함수의 로그 진폭(log-amplitude)을 Gaussian 인자로 곱했다.

---

2. Two Partial Propagations

단순히 angular-spectrum 전파를 두 번 수행한다.

• 첫 번째 전파는 source 평면에서 "middle" 평면으로 이동한다(source와 observation 평면 사이의 어딘가에 위치. 반드시 중간 위치는 아님).
• 두 번째 전파는 middle 평면에서 observation 평면으로 이동한다. absorbing boundary는 첫 번째 전파 후 middle 평면에 적용된다. 두 partial propagation 구조는 위 그림처럼 되어 있다.

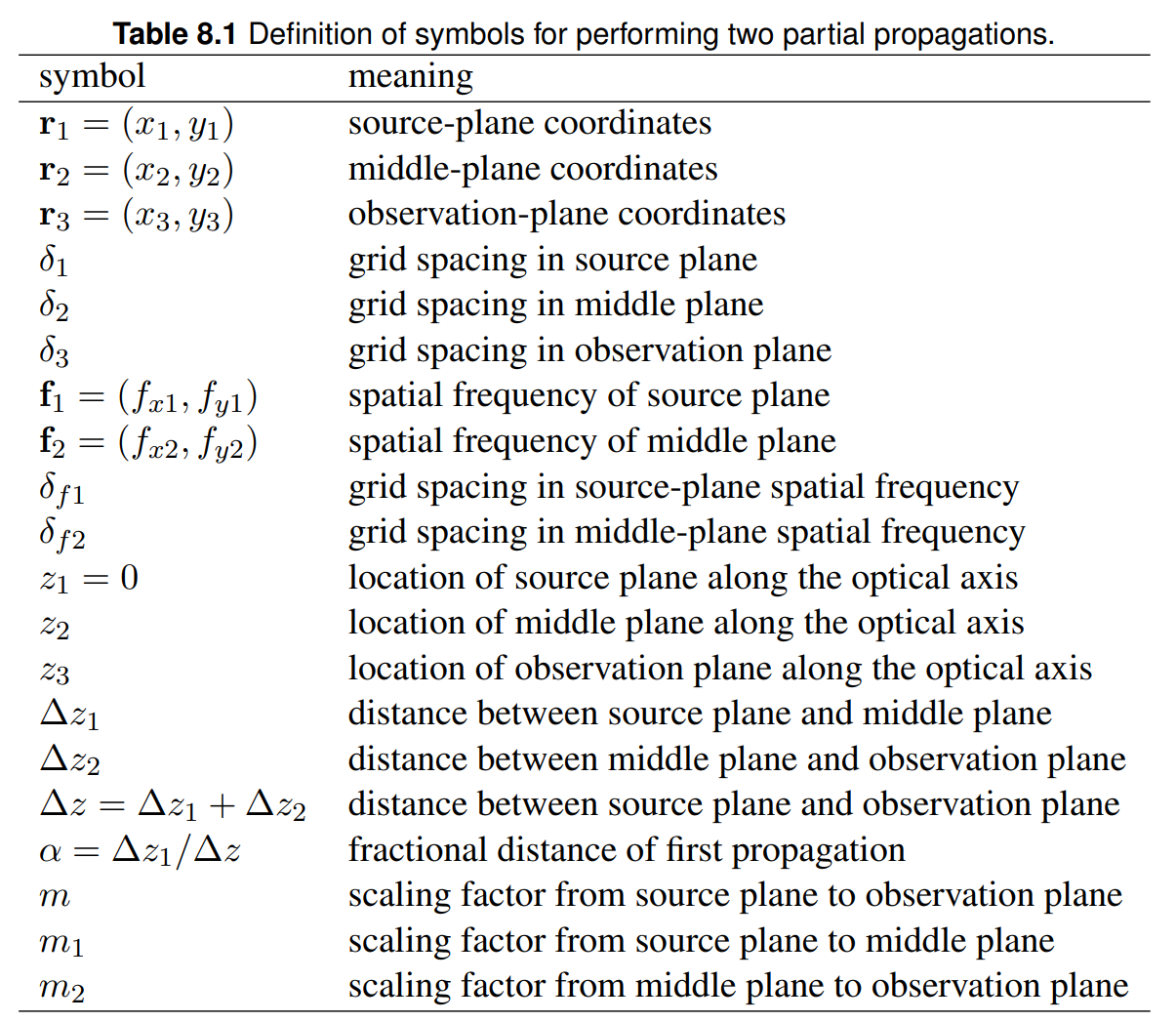
시뮬레이션 방정식에 들어가기 전에 아래 표의 기호들 사이의 수학적 관계를 결정해야 한다.

아래 그림은 grid spacings의 구조를 보여준다.

• A와 B는 source 평면의 grid points이고, $\delta_1$만큼 떨어져 있다.
• C와 D는 middle 평면의 grid points이고, $\delta_2$만큼 떨어져 있다.
• E와 F는 observation 평면의 grid points이고, $\delta_3$만큼 떨어져 있다.
• $\triangle BDH$와 $\triangle BFG$는 꼭짓점 $B$를 공유하며 닮음 관계이다. 따라서
• $\cfrac{\overline{DH}}{\overline{BH}}=\cfrac{\overline{FG}}{\overline{BG}}$

$\overline{DH}:\cfrac{\delta_2-\delta_1}{2}$, $\overline{FG}: \cfrac{\delta_3-\delta_2}{2}$, $\overline{BH}: \triangle z_1$, $\overline{BG}$: $\triangle z=\triangle z_1+\triangle z_2$

$\cfrac{\delta_2-\delta_1}{2\triangle z_1}=\cfrac{\delta_3-\delta_1}{2\triangle z}$
$\delta_2\triangle z-\delta_1\triangle z=\delta_3\triangle z_1-\delta_1\triangle z_1$
$\delta_2$에 대해 정리하면,
$\delta_2=\delta_1+\cfrac{\triangle z_1}{\triangle z}(\delta_3-\delta_1)$
$\delta_2=\delta_1+\alpha(\delta_3-\delta_1)$
$\delta_2=(1-\alpha)\delta_1+\alpha\delta_3$

지금 알려진 propagation 매개변수 사이 기본 관계를 가지고, 우리는 2가지 연속적인 전파를 수행하는 방정식을 작성할 수 있다.
middle 평면까지 $\triangle z_1$ 거리를 전파하고 $\triangle z_2$ 전파할 때, observation 평면 field $U(\mathbf{r}_3)$는 아래와 같다.

• $\mathcal{A}[\mathbf{r}_2]$는 plane 2(middle)에 field에 적용할 absorbing boundary이다. ex) super-Gaussain, Tukey 등

$U(\mathbf{r}_3)=\mathcal{Q}[\cfrac{m_2-1}{m_2\triangle z_2}, \mathbf{r}_3]\ \mathcal{F}^{-1}[\mathbf{f}_2,\cfrac{\mathbf{r}_3}{m_2}]$
$\times\mathcal{Q}_2[-\cfrac{\triangle z_2}{m_2}, \mathbf{f}_2]\ \mathcal{F}[\mathbf{r}_2,\mathbf{f}_2]\ Q[\cfrac{1-m_2}{\triangle z_2}, \mathbf{r}_2]\cfrac{1}{m_2}$
$\times\mathcal{A}[\mathbf{r}_2]\ \mathcal{Q[\cfrac{m_1-1}{m_1\triangle z_1}, \mathbf{r}_2]}\ \mathcal{F}^{-1}[\mathbf{f}_1,\cfrac{\mathbf{r}_2}{m_1}]$
$\times Q_2[-\cfrac{\triangle z_1}{m_1}, \mathbf{f}_1]\ \mathcal{F}[\mathbf{r}_1,\mathbf{f}_1]\ Q[\cfrac{1-m_1}{\triangle z_1}, \mathbf{r}_1]\cfrac{1}{m_1}\{U(\mathbf{r}_1)\}$

operator의 효과는 grid의 edge 근처에서 field의 진폭을 줄이는 함수를 field에 곱한다.

2차 phase 항들과 absorbing boundary는 모두 서로 교환법칙이 성립하며 그이유는 단지 곱셈 인자이다.
이것은 2개 middle-plane의 2차 항 인자를 합할 수 있게 하여 한 step을 제거하고 작은 연산 효율을 가져온다.

$\mathcal{Q}[\cfrac{1-m_2}{\triangle z_2},\mathbf{r}_2]\ \mathcal{Q}[\cfrac{m_1-1}{m_1\triangle z_1},\mathbf{r}_2]$

위를 합치기 위해 $\cfrac{1-m_2}{\triangle z_2}, \cfrac{m_1-1}{m_1\triangle z_1}$ 관계를 파악해야한다.

$\delta_2\triangle z_1+\delta_2\triangle z_2-\delta_1\triangle z_1-\delta_1\triangle z_2=\delta_3\triangle z_1-\delta_1\triangle z_1$

$\delta_2\triangle z_2-\delta_1\triangle z_2=\delta_3\triangle z_1-\delta_2\triangle z_1$

$\cfrac{\delta_2-\delta_1}{\triangle z_1}=\cfrac{\delta_3-\delta_2}{\triangle z_2}$

$\cfrac{\delta_2-\delta_1}{\delta_2 \triangle z_1}=\cfrac{\delta_3-\delta_2}{\delta_2 \triangle z_2}$

$\cfrac{m_1-1}{m_1 \triangle z_1}=\cfrac{m_2-1}{\triangle z_2}$

$\mathcal{Q}[\cfrac{1-m_2}{\triangle z_2},\mathbf{r}_2]\ \mathcal{Q}[\cfrac{m_1-1}{m_1\triangle z_1},\mathbf{r}_2]=\mathcal{Q}[\cfrac{1-m_2}{\triangle z_2},\mathbf{r}_2]\ \mathcal{Q}[\cfrac{m_2-1}{\triangle z_2},\mathbf{r}_2]=1$

이 특정 결과가 어떤 시뮬레이션에서도 구현되지 않지만, 임의의 수의 partial propagations에 사용할 패턴을 설정하는데 도움을 준다.

---

3. 임의의 갯수의 Partial Propagations

2개의 Partial Propagation의 parameter를 n개로 일반화하면 다음과 같다. 총 n개의 propagation planes가 있고 n-1개의 partial propagations가 있다.

그룹핑을 지으면
$U(\mathbf{r}_3)=\mathcal{Q}[\cfrac{m_2-1}{m_2\triangle z_2}, \mathbf{r}_3]\ \{\mathcal{F}^{-1}[\mathbf{f}_2,\cfrac{\mathbf{r}_3}{m_2}]\ \mathcal{Q}_2[-\cfrac{\triangle z_2}{m_2}, \mathbf{f}_2]\ \mathcal{F}[\mathbf{r}_2,\mathbf{f}_2]\ \cfrac{1}{m_2}\}$
$\times\{\mathcal{A}[\mathbf{r}_2]\ \ \mathcal{F}^{-1}[\mathbf{f}_1,\cfrac{\mathbf{r}_2}{m_1}]\ Q_2[-\cfrac{\triangle z_1}{m_1}, \mathbf{f}_1]\ \mathcal{F}[\mathbf{r}_1,\mathbf{f}_1]\ \cfrac{1}{m_1}\}$
$\times \{Q[\cfrac{1-m_1}{\triangle z_1}, \mathbf{r}_1]\ U(\mathbf{r}_1)\}$

각 partial 전파에서 operation이 반복된다. 이를 $n-1$ partial propagations에 일반화시켜 적용하면,
$U(\mathbf{r}_n)=\mathcal{Q}[\cfrac{m_{n-1}-1}{m_{n-1}\triangle z_{n-1}}]\{\mathcal{F}^{-1}[\mathbf{f}_{n-1},\cfrac{\mathbf{r}_n}{m_{n-1}}]\ \mathcal{Q}_2[-\cfrac{\triangle z_{n-1}}{m_{n-1}}, \mathbf{f}_{n-1}]\ \mathcal{F}[\mathbf{r}_{n-1}, \mathbf{f}_{n-1}]\cfrac{1}{m_{n-1}}$
$\times \prod_{i=1}^{n-2}\{ \mathcal{A}[\mathbf{r}_{i+1}]\ \mathcal{F}^{-1}[\mathbf{f}_{i}, \cfrac{\mathbf{r}_{i+1}}{m_i}]\ \mathcal{Q}_2[\cfrac{-\triangle z_{i}}{m_i},\mathbf{f}_i]\ \mathcal{F}[\mathbf{r}_{i},\mathbf{f}_{i}] \cfrac{1}{m_i} \}$
$\times \{\mathcal{Q}[\cfrac{1-m_1}{\triangle z_1}, \mathbf{r}_1]\ U(\mathbf{r}_1) \}$

---

4. Sampling for Multiple Partial Propagations

임의의 갯수의 plane과 반복되는 partial propagations가 있으면 sampling 제약조건은 다시 검토된다.
하나의 완전한 propagation에서는 선택한 grid point 갯수와 선택한 grid spacings가 4가지 부등식을 만족했어야 했다.
constraint1,2 부등식은 propagation geometry 기반이었고 전파 방법에 따른 것은 아니다.
그래서 multiple partial propgations를 사용할 때는 constraint 1,2 부등식은 그대로 유지된다.
하지만 나머지 constraint 3,4 부등식은 grid spacings와 propagation 거리에 의존하며 2차 phase 인자의 aliasing을 막는다.
grid spacings와 propagation 거리는 모든 partial propagation에서 변할 수 있고, 따라서 접근법을 달리해야 된다.

constraint 3는 angular-spectrum method의 FT 안의 2차 phase 인자의 aliasing을 막기 위해서다. 여기에 같은 개념을 적용하면, 지름 $R$의 구면 source wavefront라고 가정하면 source field와 2차 phase 인자의 조합 phase는
$\phi=\cfrac{k}{2}(\cfrac{1-m}{\triangle z_1}+\cfrac{1}{R})|\mathbf{r}_1|^2$

우선, constraint3은 $\triangle z_1$에 의존하기 때문에 혼란스럽지만, 남은 sampling 분석이 완료될 때까지 $\triangle z_1$을 결정할 수 없다. 그럼에도 불구하고, 분석을 계속해본다.
$(1+\cfrac{\triangle z_1}{R})\delta_1-\cfrac{\lambda\triangle z_1}{D_1}\le\delta_2\le(1+\cfrac{\triangle z_1}{R})\delta_1+\cfrac{\lambda\triangle z_1}{D_1}$

$\delta_2$와 $\triangle z_1$을 치환하면
$(1+\cfrac{\alpha_2 \triangle z}{R})\delta_1-\cfrac{\lambda\alpha_2 \triangle z}{D_1}\le(1-\alpha_2)\delta_1+\alpha_2\delta_n\le(1+\cfrac{\alpha_2 \triangle z}{R})\delta_1+\cfrac{\lambda\alpha_2 \triangle z}{D_1}$

$\delta_n$에 대한 부등식으로 정리하고
$(\cfrac{\alpha_2 \triangle z}{R})\delta_1-\cfrac{\lambda\alpha_2 \triangle z}{D_1}+\alpha_2\delta_1 \le\ \alpha_2\delta_n\le(\cfrac{\alpha_2 \triangle z}{R})\delta_1+\cfrac{\lambda\alpha_2 \triangle z}{D_1}+\alpha_2\delta_1$

부등식 $\alpha_2$로 나눠주기
$(\cfrac{\triangle z}{R}+1)\delta_1-\cfrac{\lambda \triangle z}{D_1} \le\ \delta_n\le(\cfrac{\triangle z}{R}+1)\delta_1+\cfrac{\lambda\triangle z}{D_1}$

결과적으로 multiple partial propagation이나 angular-spectrum propagation constraint 3은 같다.
즉 $\delta_2$와 $\triangle z_1$ partial-propgation 평면 갯수에 관계없다.

constrain4의 경우 n과의 관계를 찾아보면 $i^{th}$ partial propagation에 대해
$N\ge\cfrac{\lambda \triangle z_i}{\delta_i\delta_{i+1}}$

이것은 매우 복잡한 parameter space를 만드는데,간소화하기위해 모든 $\delta_i$는 $\delta_1$과 $\delta_n$에 대한 식으로 표현할 수 있다.
$\delta_i=(1-\alpha_{i})\delta_{1}+\alpha_{i}\delta_n$

하지만, $\delta_i$를 단순히 $\alpha_i$를 교환한것 밖에 안되고 여전히 $z_i$이다.

constraint에 대한 parameter space의 차원을 줄일 수 있는 방법은 없다.
위 부등식이 암시하는 모든 n에 대한 제약조건을 만족하기 위하는 것보다, 오직 우변이 최대로 되는 case만이 필요하다.
하지만, 이것도 모든 $\triangle z_i$와 $\delta_i$에 대한 사전지식이 필요하다.

명백히 새로운 접근법이 필요한데, constraint 1~4를 다시 써보면

1. $\delta_n\le\cfrac{\lambda\triangle z-D_2\delta_1}{D_1}$
2. $N\ge\cfrac{D_1}{2\delta_1}+\cfrac{D_2}{2\delta_n}+\cfrac{\lambda\triangle z}{2\delta_1\delta_n}$
3. $(\cfrac{\triangle z}{R}+1)\delta_1-\cfrac{\lambda \triangle z}{D_1} \le\ \delta_n\le(\cfrac{\triangle z}{R}+1)\delta_1+\cfrac{\lambda\triangle z}{D_1}$
4. $N\ge\cfrac{\lambda\triangle z_i}{\delta_i\delta_{i+1}}$

$N, \delta_1, \delta_n$ 값을 선택하기 위해 constrain 1,2,3 부등식을 이용할 가능성이 있다. 그리고 4번째 constraint을 만족하는 방법을 찾아보자.

propagation grids를 확장할지 줄어들게 사용할 지에 따라, $\delta_1$ 또는 $\delta_n$이 다른 모든 $\delta_i$보다 작을 수 있다.

$\triangle z_i$ 값이 주어졌을 때, $\delta_i$와 $\delta_{i+1}$을 4번째 부등식에서 대체하기 위해 작은 $\delta_1$과 $\delta_n$을 선택하는 것은 $N$을 만족해야 하는 하나의 제약조건을 줄 수 있다.

하지만, $N$은 constraint 1,2을 사용하여 선택되고, $\triangle z_i$가 한계로 남아있는데, 이에 대한 부등식은
$\triangle z_i\le\cfrac{min(\delta_1, \delta_n)^2N}{\lambda}$
우변은 최대 가능한 partial-propgation distance $\triangle z_{max}$이다.
그러므로 partial propagations 적어도 $n=ceil(\cfrac{\triangle z}{\triangle z_{max}}+1)$개 사용해야 한다.

최종적으로, 4번째 부등식은 propagation-grid parameter를 정하는 방법은

1. constraint 1,2를 기반으로 $N, \delta_1,\delta_n$을 선택한다.
2. 4번째 부등식의 살짝 조정된 $\triangle z_i\le\cfrac{min(\delta_1, \delta_n)^2N}{\lambda}$
   부등식을 사용하여 최대 partial-propagation 거리와 최소 propagation 수 $n-1$를 같이 구한다.
3. 더 많은 partial propagations 을 사용할 수 있다. 더 짧은 partial-propation distance는 여전히 4번째 부등식을 충족한다.

---

5. Simulation Code