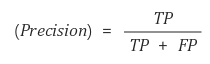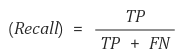End-to-End Object Detection with Transformers(DETR)

Dr.Pepper·2024년 11월 26일

DETR Object Detection end-to-end transformer

오늘 review해 볼 논문은 2020년도에 나온 DETR입니다!

제목 : End-to-End Object Detection with Transformers(DETR)
저자 : Nicolas Carion et al.
학회 : EECV 2020
게제 년도 : 2020년
인용수 : 14,623회

0. 필수 개념

먼저 IoU와 GIoU에 대해서 알아보겠습니다!

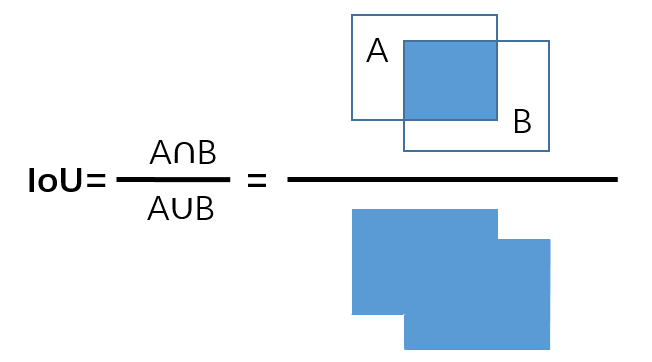
IoU(Intersection over Union)

예측 bounding box와 ground truth가 일치하는 정보를 0과 1 사이의 값으로 나타낸 값입니다

Box가 겹치지 않으면 떨어진 정도를 반영할 수 없습니다
-> box가 떨어져 있으면, 떨어진 거리와 관계 없이 동일한 loss 0이 부여됩니다

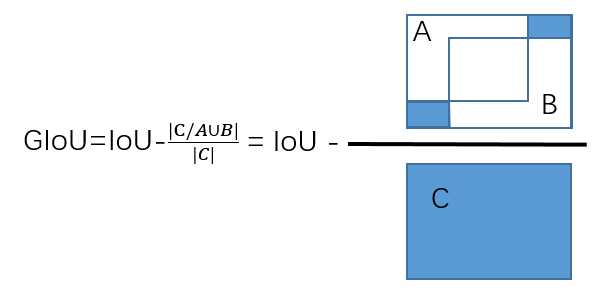
GIoU

IoU를 개선시킨 것으로, bounding box와 ground truth를 모두 포함하는 최소 크기의 C box를 이용합니다

Box가 겹치지 않은 경우(IoU=0)에도 loss를 정의해 학습에 이용할 수 있습니다(-1 ~ 1 사이의 값)

다음으로는 precision과 recall에 대해서 알아보겠습니다!

Precision

예측을 positive로 한 애들 중에서, 예측 값과 실제 값이 일치하는 데이터의 비율입니다

Box 친 애들 중 제대로 class를 예측한 애들의 비율입니다

Detection한 결과가 실제 Object들과 얼마나 잘 일치하는가?를 나타냅니다

예측을 한 데이터가 기준입니다

Recall

실제 값이 positive한 애들 중에서, 예측 값과 실제 값이 positive로 일치하는 데이터의 비율입니다

실제 Object 중 Box를 제대로 친 애들의 비율입니다

실제 Object들을 빠뜨리지 않고 얼마나 정확히 Detection 했는가?를 나타냅니다

실제 Object가 기준입니다

이번에는 Precision-Recall의 변화 및 AP에 대해서 알아보겠습니다!

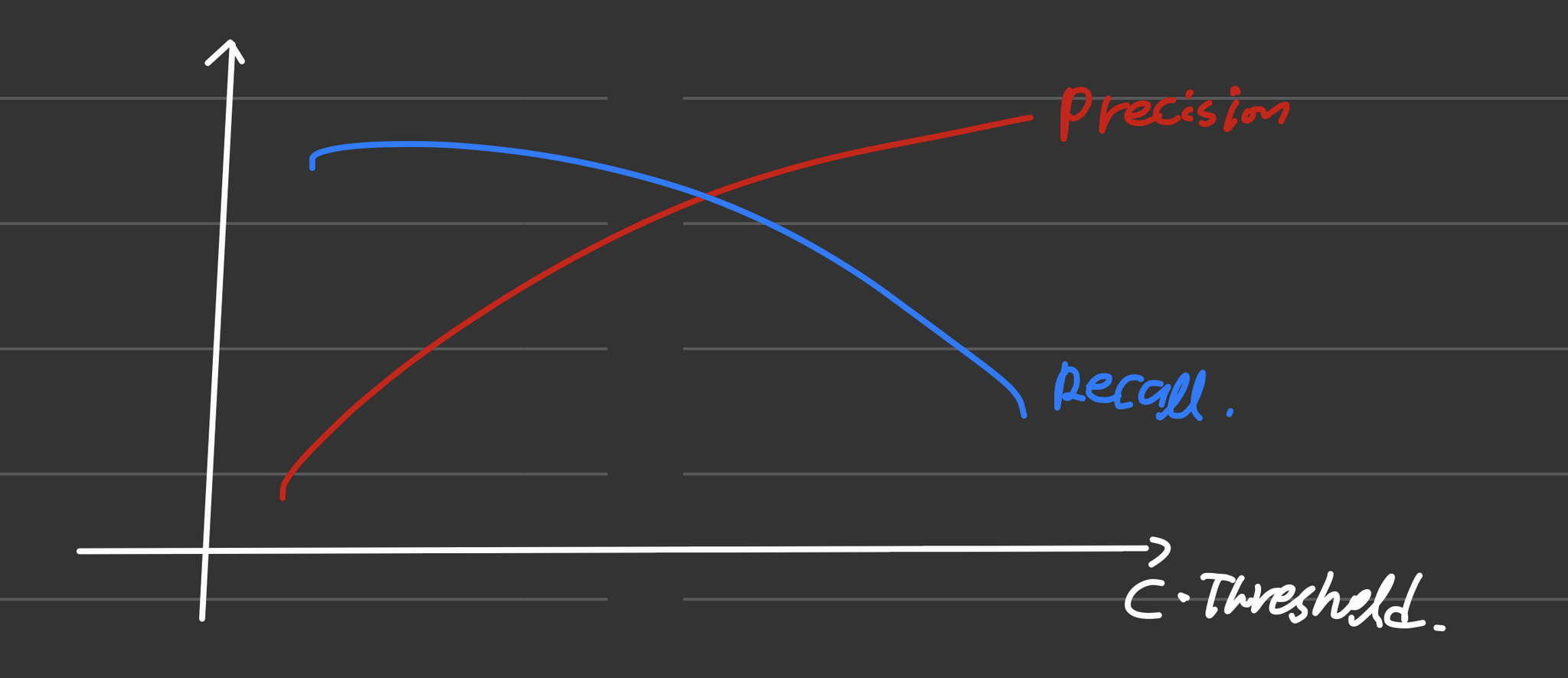
Confidence Threshold에 따른 Precision-Recall 변화

Confidence : 모델마다 주로 C로 등장하는, 해당 예측이 얼마만큼의 신뢰도를 가지는지를 나타내는 점수입니다(이 정도 확률로 예측한다..)

Confidence Threshold : Confidence의 임계값으로, Confidence가 몇 이상인 예측들만 예측으로 볼 것인지에 대한 수치입니다
(1) C.Threshold가 낮으면 Box 예측이 많아짐(난사) -> Precision 감소, Recall 증가
(2)C.Threshold가 높으면 Box 예측이 적어짐(신중) -> Precision 증가, Recall 감소

Confidence Threshold에 따라 Precision과 Recall의 Trade-off가 있습니다

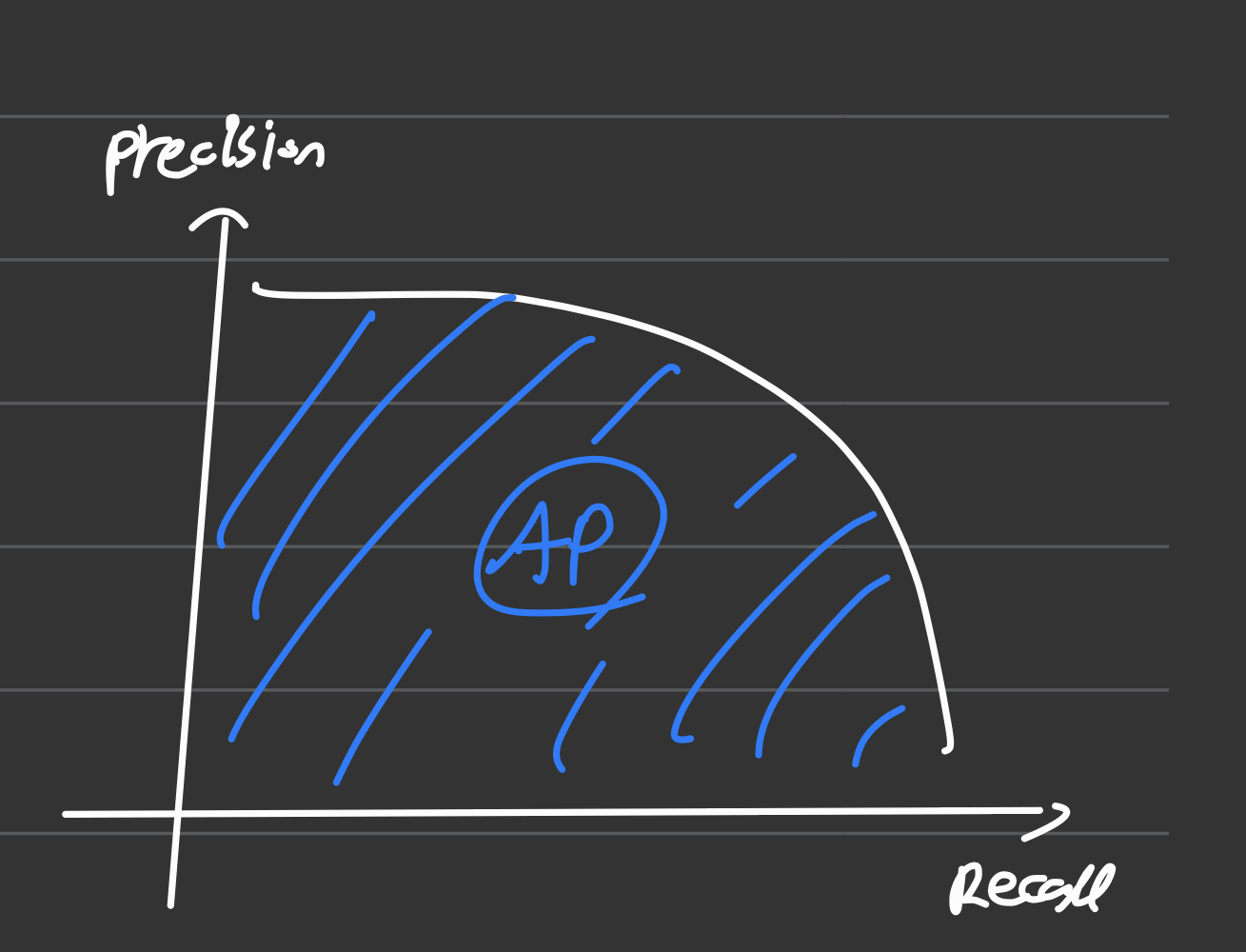
Precision-Recall Curve와 AP(Average Precision)

Precision-Recall Curve는 Recall의 변화에 따른 Precision을 나타낸 곡선입니다.

X축은 Recall을 나타내고, Y축은 Precision을 나타냅니다

이때 Precision-Recall Curve의 면적이 AP(Average Precision)라고 할 수 있습니다
-> 즉 AP는 Precision 값들의 평균이라고 볼 수 있습니다

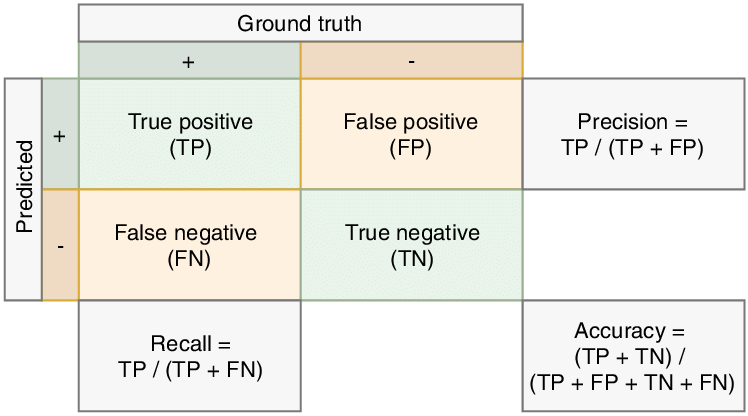
다음으로는 Confusion Matrix(오차 행렬)에 대해서 알아보겠습니다!

Confusion Matrix는 이진 분류에서의 예측을 유형별로 나눈 것입니다.

FP : 실제 없는 것에 box를 치거나 class를 예측한 것입니다

FN : 있는 object에 대해 box를 안 친 것입니다

TP : Box도 잘치고, class 예측도 잘 한 것입니다

TN : 지표에 쓰이지 않습니다

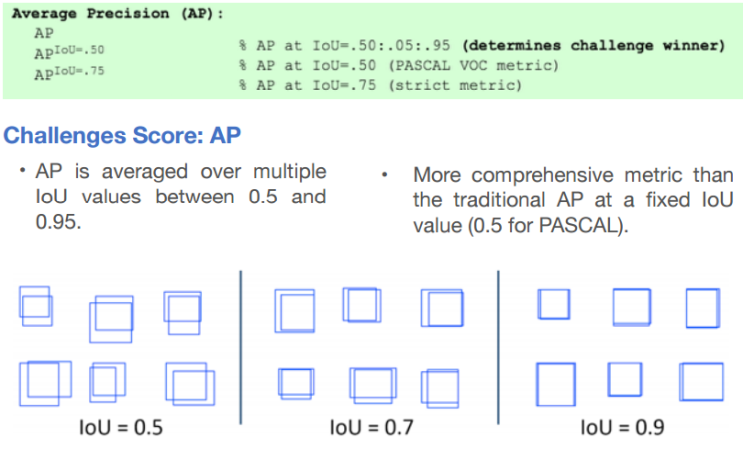
마지막으로 mAP에 대해서 알아보겠습니다!

mAP : 여러 Object들에 대한 AP의 평균입니다
-> AP : 1개의 Object class에 대한 수치입니다
AP[.50:.05:.095] : IoU를 기준으로 0.5부터 시작해서 0.95까지 0.05씩 높이면서 측정한 mAP를 나타냅니다
-> AP@[.50:.05:.095]로 표기하기도 합니다

AP50 : IoU의 최솟값이 0.5

AP75 : IoU의 최솟값이 0.75

1. Preview

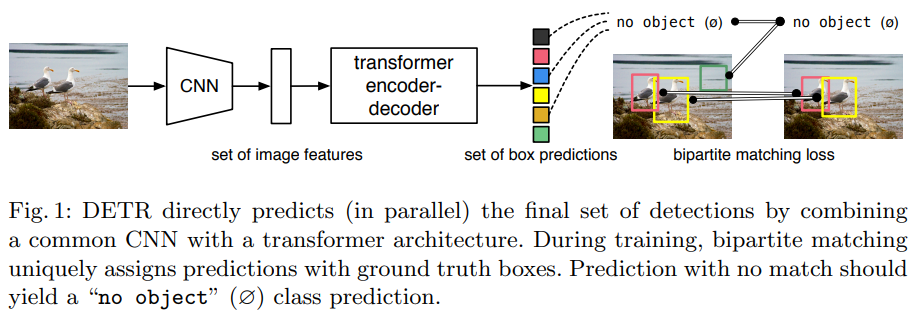
먼저 본 논문의 Contribution에 대해서 간단하게 알아보고 넘어가도록 하겠습니다

(1) Direct set prediction
-> Object Detection을 Direct Set Prediction으로 정의해, Transformer와 Bipartite matching loss를 사용한 DETR을 제안했습니다.

(2) Faster R-CNN과 비슷한 성능
-> COCO dataset에 대하여 Faster R-CNN과 비슷한 수준의 성능을 보였습니다.

(3) 크기가 큰 객체 포착 성능 우수
-> Self-Attention을 통한 Global Information(전역 정보)을 활용함으로써, 크기가 큰 Object를 Faster R-CNN보다 훨씬 잘 포착 가능합니다.

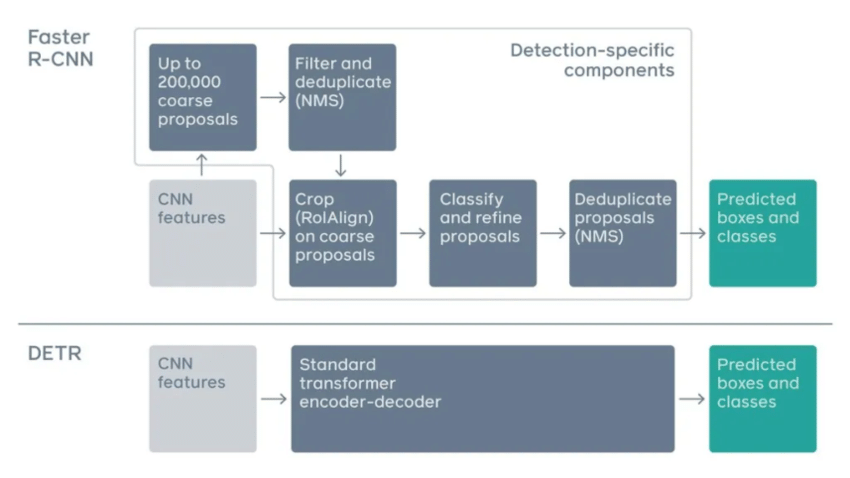
2. 기존 방법의 한계

1. 기존 방법

기존 방법은 Regression, Anchor, Window 등을 이용해 proposal을 찾은 뒤, 중복을 제거하는 과정을 사용하는 Indirect Way를 사용했습니다.

그렇기 때문에 중복되는 prediction을 피하기 위해 Post-Processing이 많이 사용되었습니다.

2. 한계점

이러한 기존 방법의 한계점에 대해서 알아보겠습니다.

기존 방법은 RPN, NMS 등 미리 hand-design 되어야 하는 prior knowledge가 생긴다는 한계가 있었습니다
-> 이때 RPN, Anchor Box, NMS는 몇 천개의 영역을 처리해야 합니다(pos-processing)

또한 pipeline이 복잡하고 End-to-End 구조라고 보기 힘들다는 한계점이 존재했습니다

3. DETR Architecture

본 논문에서는 Transformer(Encoder, Decoder) + Bipartite matching(Hungarian Algorithm)을 제안했습니다.

(1) Prediction bounding box와 Ground truth box 사이의 unique한 matching을 가능하도록 하는 set prediction loss를 이용합니다.

(2) 한 번의 forward pass로 object model 사이의 relation을 예측하는 architecture를 사용합니다.(End-to-End)

(1) Predicted bounding box와 ground box 사이의 unique한 matching 수행
(2) Matching된 결과를 기반으로 Hungarian loss 연산

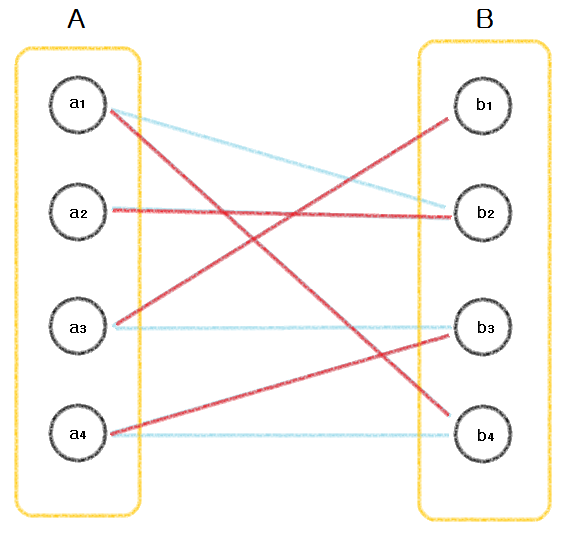
Bapartite Matchin(Hungarian Algorithm)이 무엇인지 대해 알아보겠습니다.

Bipartite Matching은 일대일로 중복이 허용되지 않는 matching을 수행합니다.

Object query마다 예측된 결과물과 ground truth간 Hungarian Algorithm 기반 matching을 수행합니다.

-> Set Prediction과 Ground truth 간 일대일 matching을 수행하여 중복을 배제합니다.

-> 빨간 선일때 이분 매칭입니다.

이번에는 Object Detection set prediction loss에 대해 알아보겠습니다

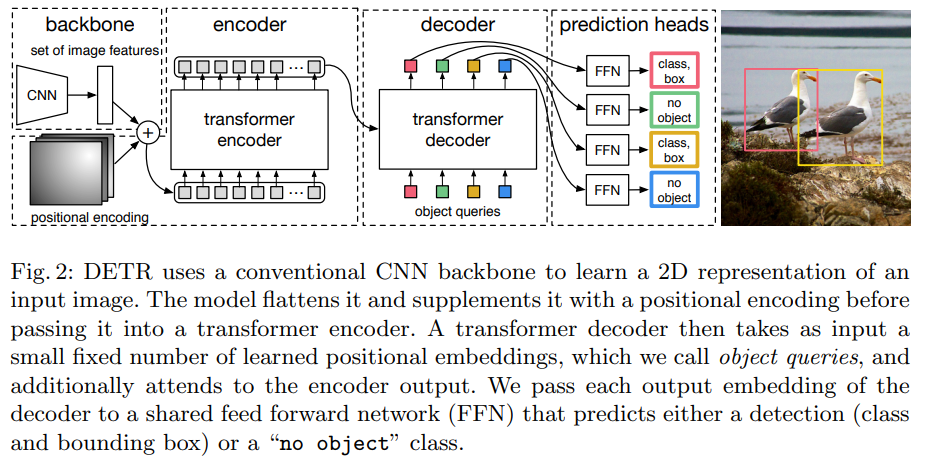
좀더 Architecture에 대해서 자세히 알아보겠습니다

(1) CNN Backbone : Transformer에 들어가는 Feature map을 뽑아냅니다(ResNet 50,101을 사용합니다)
(2) Transformer Encoder, Decoder
-> Encoder : 같은 instance끼리 높은 attention을 가집니다.
-> Decoder : box에 접하는 부분이 높은 값을 가집니다(말단 부분을 잘 학습합니다)
(3) FFN(Feed Foward Network) : FNN을 통과하여 Class와 Box를 예측합니다(Bipartite matching을 수행합니다)

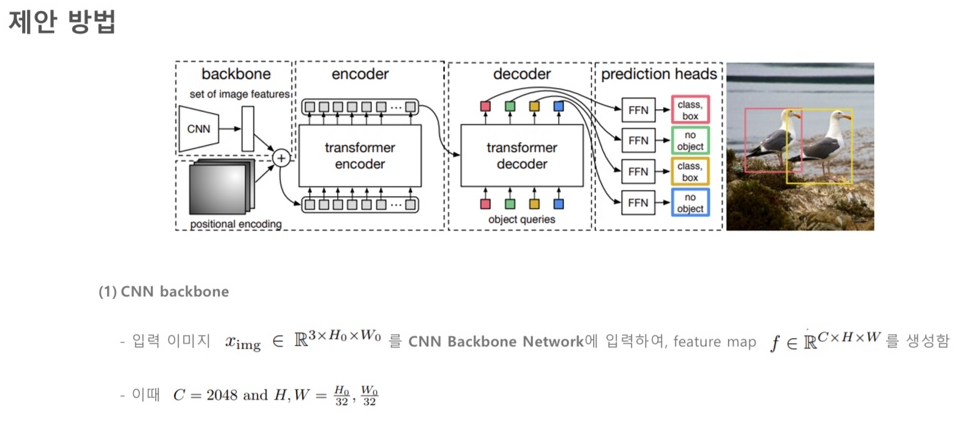
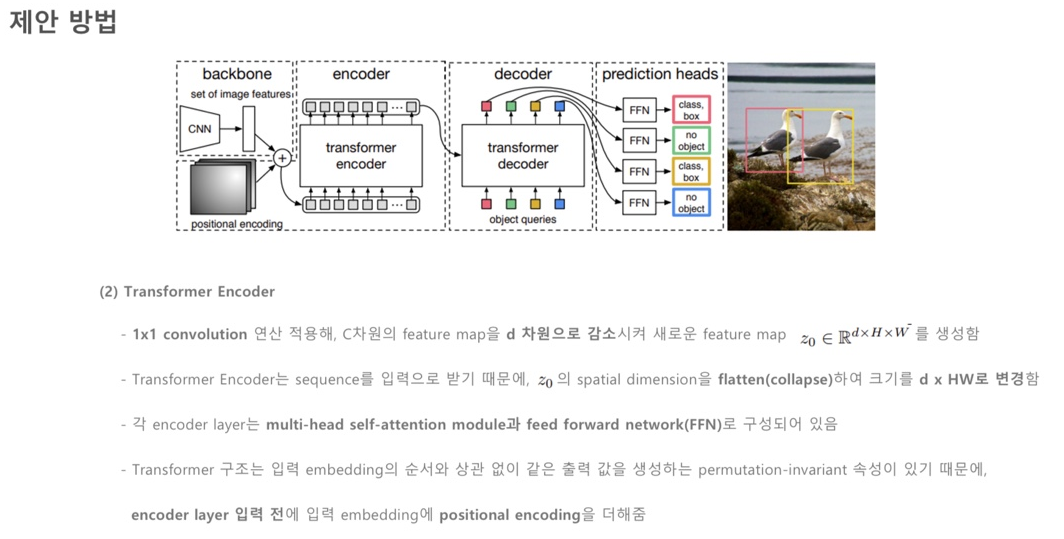
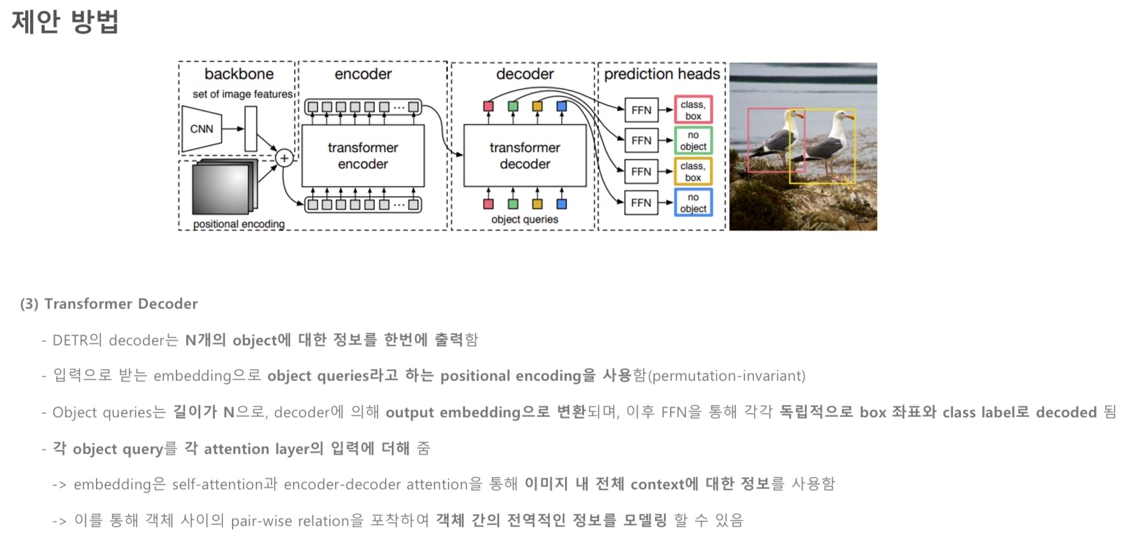
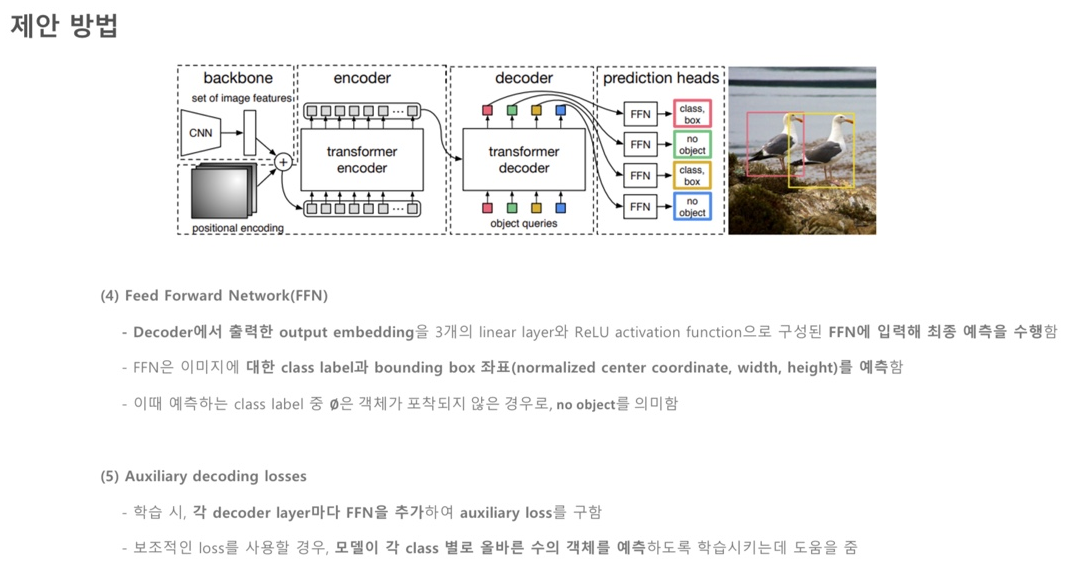
4. Experiment

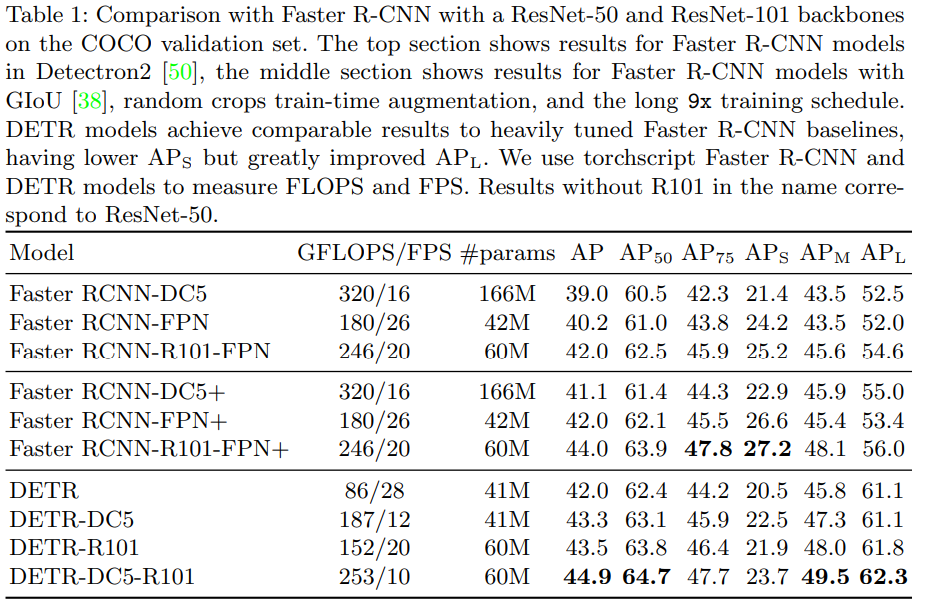
COCO 데이터셋을 통해 Faster R-CNN과 DETR 결과를 비교한 표입니다.
결과를 보면 DETR이 SOTA인 Faster R-CNN과 견줄만한 성능을 내는 것을 확인할 수 있습니다.
하지만 큰 물체는 잘 구분하지만, 작은 물체는 상대적으로 성능이 떨어지는 것을 알 수 있습니다.

GFLOPS : 부동소수점 초당 연산량입니다
FPS : 모델이 얼마나 빠르게 동작하는지 측정합니다
AP : precision-recall 그래프의 아래쪽 면적입니다
AP50 : IoU 최솟값 0.5
AP 75 : IoU 최솟값 0.75

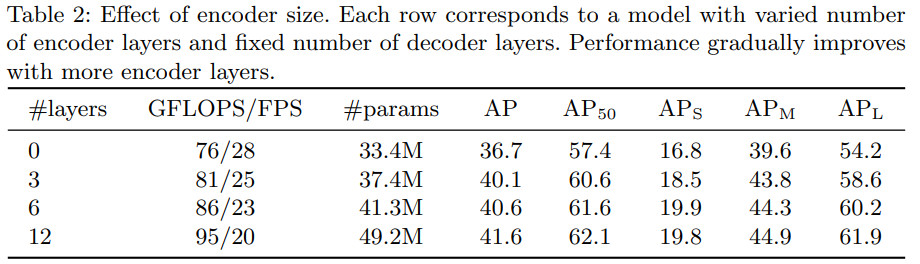
Encoder 크기의 영향에 대해 보여주는 표입니다.
Encoder size가 커짐에 따라서 성능이 증가하는 것을 알 수 있습니다.
Decoder가 고정되어 있는 상태에서 Encoder가 커질수록 성능이 증가하는 것을 확인할 수 있습니다.

Encoder self-attention을 시각화한 그림입니다.
마지막 layer에서의 attention map을 이용한 encoder의 self-attention 출력을 시각화한 그림입니다.
각각의 개별 instance를 잘 분리하는 것을 알 수 있습니다.

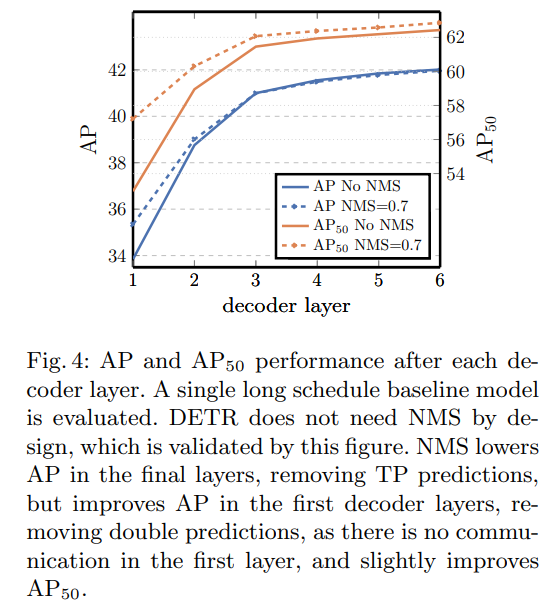
Decoder layer에 따른 AP 성능을 보여주는 그림입니다.
Decoder layer가 깊어질수록 좋은 성능을 보이는 것을 알 수 있습니다.
NMS와 거의 비슷한 성능을 내는 것을 확인할 수 있습니다
-> 이는 Object 간의 관계를 더 잘 학습하고, Bipartite matching 기반 Hungarian loss 사용하기 때문에 나타납니다.

일반화와 관련된 그림입니다.
훈련 데이터에 없던 이미지도 잘 분류하는 것을 알 수 있습니다.
-> 즉 일반화가 잘 된다는 것을 확인할 수 있습니다.

Decoder attention 시각화에 대한 그림입니다
그림을 보면, 말단 정보를 잘 캐치하는 것을 알 수 있습니다.
-> Attention을 적용함으로써, 전체 boundary에 대한 외곽 부분을 잘 캐치해 내고 학습이 이루어지는 것을 확인할 수 있습니다.
Box를 찾아내는 데에 중요한 부분들에 많은 attention을 주고 있는 것을 알 수 있습니다.

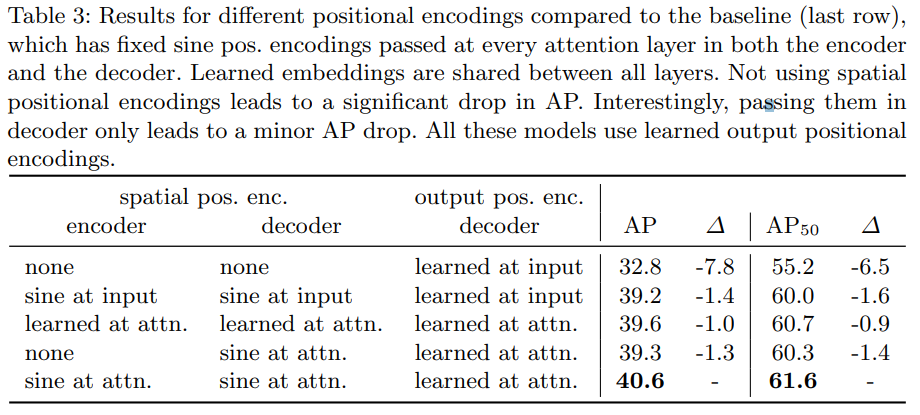
Positional encoding의 결과에 대한 표입니다.
여기서 델타 값은 감소량을 나타냅니다
Positional encoding을 사용하지 않으면 AP가 크게 떨어지는 것을 알 수 있습니다.
Decoder에 전달하면 약가늬 AP 저하만 발생하는 것을 알 수 있습니다.
위치에 대한 정보를 많이 가지고 있는 Positional Encoding의 중요성을 확인할 수 있습니다.

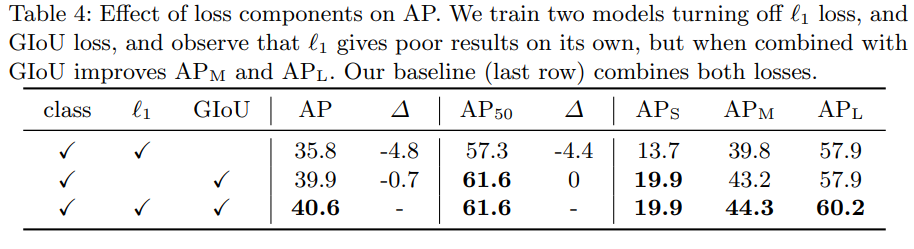
Loss 구성이 AP에 미치는 영향에 대해 나타낸 표입니다.
각 loss function을 어떻게 구성하는지에 따라서 accuracy 차이가 발생하는 것을 알 수 있습니다.
현재 사용되고 있는 loss 값의 구성의 중요성을 나타냅니다.
GIoU가 모델의 성능을 계산하는데 중요한 역할을 수행하는 것을 알 수 있습니다.
L1 loss를 사용하지 않고, GIoU만 사용해도 AP에 큰 차이가 없는 것을 확인할 수 있습니다.

실제 Box prediction에 대한 시각화에 관한 그림입니다.
N개의 object query가 있을 때, 20개만 뽑아서 보여줍니다.
점들은 각각 bounding box의 center 값입니다.
어느 부분에 더 많은 관심을 가지고 인식하는지, 더 많은 가중치를 주어 인식하는지 등을 알 수 있습니다.
Object가 있는 위치에 따라, 동일한 위치의 Object Query가 활성화됩니다.

5. Conclusion

1. 결론

Object Detection을 Direct Set Prediction의 관점에서 새롭게 접근한 모델을 제안했습니다
Detection + Transformer로 Bipartite matching과 Transformer를 활용한 End-to-End 모델을 제안했습니다
DETR은 확장성이 뛰어나고, SOTA인 Faster R-CNN과 견줄만큼의 충분히 competitive한 성능을 보였습니다

2. 한계점

Transformer의 Attention을 이용하기 때문에 긴 학습 시간을 가지고 있다는 한계점이 있습니다
Transformer는 global한 context를 잘 인식하는 특징을 가지고 있어 큰 object는 잘 구분하지만, 작은 object는 잘 구분하지 못하는 한계점을 가지고 있습니다