1. 다중회귀분석

1. 다중회귀분석(Multiple Regression Analysis)

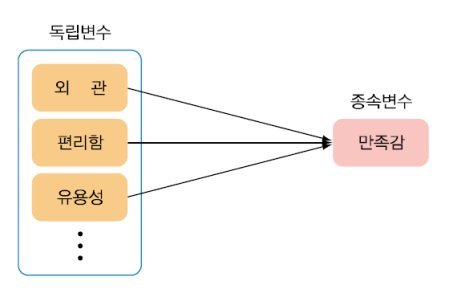
• 여러 개의 독립변수 X가 종속변수 Y 에 미치는 영향을 회귀식(회귀방정식)을 이용하여 분석하는 방법
  

• 단순선형 회귀가 하나의 독립변수를 다룬다면 다중선형 회귀는 여러 개의 독립변수 를다룸

• 예. 키와 몸무게를 가지고 혈당 수치를 예측하는 문제

  • 독립변수: 키, 몸무게
  • 종속변수: 혈당수치(y)

• 다중 회귀모형 (다중 회귀식)의 일반적인 형태
  

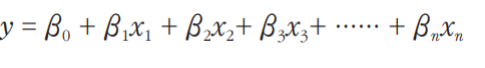
2. 가정사항

• 수집된 데이터가 정규분포를 따른다. (정규성의 가정)
• 오차항(잔차)의 분산은 모두 동질적이다. (등분산성의 가정)
• 데이터는독립적으로추출되어야한다. (독립성의 가정)

3. 다중공선성(MuItic011inearity)

• 독립변수 간의 관계는 독립이라는 가정사항을 만족하지 못하는 경우
• 즉, 독립변수들 간에 상관관계가 높은 경우 다중회귀모형의 추정에 영향을 미침
  • 해당 독립변수가 종속변수에 실제로 유의한 영향력을 미치더라도 회귀계수의 영향력이 유의하지 않은 것으로 나타날 수 있음
  • 회귀계수의 추정값을 신뢰할 수 없음
    -결정계수는 높지만 제대로 된 회귀모형을 추정하지 못함, 오자가 존재할 수 있음
• 다중회귀분석의 VIF(\/anance lnflation)값을 통해 확인
  • VIF < 10 일 때 다중공선성 문제가 없다고 판단
  • VIF가 10 이상인 변수가 존재하면, 해당 변수를 제외하고 재분석

4. 데이터의 관련성 확인

• 산점도를 이용하여 변수 간 관련성을 먼저 확인
• 상관계수 행렬을 통해 종속변수와 관련성이 높은 변수를 파악
  

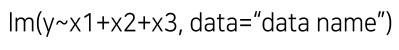
5. R을 이용한 다중 회귀분석

산포도(Scatter Diagram)

# data 입력
x1 <- c(7,3,3,4,6,7,2,7,30,5,16,10,4,6,9,10,6,7,3,17,10,26,9,8,4)
x2 <- c(560,220,340,80,150,330,110,210,1460,605,688,215,255,462,448,
 776,200,132,36,770,140,810,450,635,150)
y <- c(16.68,11.5,12.03,14.88,13.75,18.11,8,17.83,79.24,21.5,40.33,21,
 13.5,19.75,24,29,15.35,19,9.5,35.1,17.9,52.32,18.75,19.83,10.75)
# data frame 만들기
sampleData <- data.frame(x1,x2,x3,y)
# plot 함수를 이용하여 산점도 그리기
plot(sampleData)

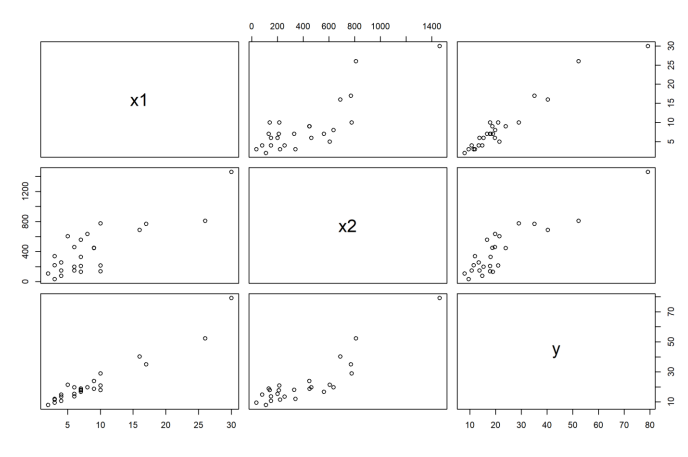
상관행렬(Correlation Matrix)

# 변수별 상관행렬 구하기
cor(sampleData)
> cor(sampleData)
x1 x2 y
x1 1.0000000 0.8242150 0.9646146
x2 0.8242150 1.0000000 0.8916701
y 0.9646146 0.8916701 1.0000000

다중선형 회귀분석(Multiple Linear Regression Analysis)

# 회귀함수인 lm( ) 함수 호출
fit <- lm(y ~ x1+x2)
# 결과 출력
summary(fit)

summary(fit)
Call:
lm(formula = y ~ x1 + x2)
Residuals:
Min 1Q Median 3Q Max
-5.7880 -0.6629 0.4364 1.1566 7.4197
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.341231 1.096730 2.135 0.044170 *
x1 1.615907 0.170735 9.464 3.25e-09
x2 0.014385 0.003613 3.981 0.000631
Signif. codes: 0 ‘*’ 0.001 ‘’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.259 on 22 degrees of freedom
Multiple R-squared: 0.9596, Adjusted R-squared: 0.9559
F-statistic: 261.2 on 2 and 22 DF, p-value: 4.687e-16

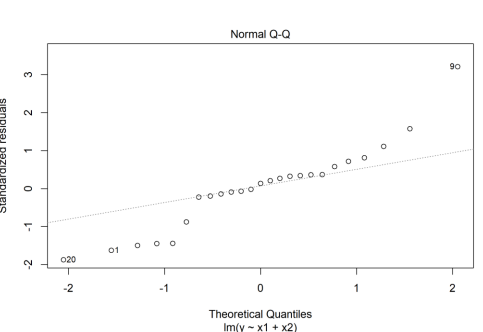
# 잔차의 정규성 검정(Shapiro test)
reg=residuals(fit)
shapiro.test(reg)
Shapiro-Wilk normality test
data: reg
W = 0.95151, p-value = 0.2711

# 잔차의 독립성 검정(Durbin-Watson test)
install.packages("lmtest")
library(lmtest)
dwtest(fit)
Durbin-Watson test
data: fit
DW = 1.1696, p-value = 0.01202
alternative hypothesis: true autocorrelation is greater than 0

# 다중공선성 검정
install.packages(“car")
library(car)
vif(fit)
vif(fit)
 x1 x2
3.118474 3.118474

# 계수 값 출력
fit$coef
(Intercept) x1 x2
2.34123115 1.61590721 0.01438483
# 독립변수 X1, X2에 대응되는 예측 값 출력
fit$fitted
# 독립변수 X1, X2에 대응되는 잔차 (=실제값-예측값) 출력
fit$resid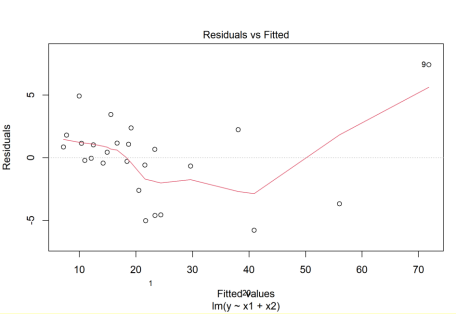

2. 변수선택법

1. 변수 선택 (VariabIe SeIection)

• 선형 회귀 모형을 만들 때 주어진 여러 변수 중 어떤 변수를 설명변수로해야 할지는 연구자의 배경 지식으로 결정
• 이러한 배경지식이 없거나 또는 정확히 결정할 수 없을 때는 변수 선택법을 이용해서 선택

1. 전진 선택법
2. 후진 소거법
3. 단계적 방법

• 변수 선택 (모형 평)h) 기준 : AlC(Akaike lnformation Criterion),
  BIC(Bayes lnformation Criterion), Cp(MaIIOW's Cp)

• AIC 혹은 BIC를 최소화 시키는 모형 최적의 모형

• 전진 선택법 (forward selection) : 절편만 있는 모형에서 기준 통계 값을 가장 많
  이 개선시기는 변수를 사례로 추가하는 방법

  • 설명변수가 없는 상태에서 설명변수를 하나씩 추가해나가는 방법
  • 추가되는 설명변수의 기여도가 통계적으로 유의하지 않을 때 중단
  • 후진 소거법(backward eliminatlon): 모든 변수가 포함된 모형에서 기준 통계
    값에 가장 도움이 되지 않는 변수를 하나씩 제거하는 방법
  • 처음에는 모든 설명변수를 사용하며 시작해 단계별로 가장 유용하지 않은 변수를 하나씩 제거해나가는 방법
  • 제거되지 않고 남아있는 설명변수들의 기여도가 모두 유의하다고 판단될 때 중단

• 단계적방법(stepwise selection): 모든 변수가포함된모형에서 출발하여 기준 통계 값에 가장 도움이 되지 않는 변수를 삭제하거나, 모형에서 빠져 있는 변수 중에서 기준 통계치를 가장 개선시기는 변수를 추가함

2. R: Variable Selection

3. R예제

변수선택법

# stepAIC 함수 제공
library(MASS)
# data 생성
x1 <- c(1.74,6.32,6.22,10.52,1.19,1.22,4.1,6.32,4.08,4.15,10.15,1.72,1.7)
x2 <- c(5.3,5.42,8.41,4.63,11.6,5.85,6.62,8.72,4.42,7.6,4.83,3.12,5.3)
x3 <- c(10.8,9.4,7.2,8.5,9.4,9.9,8,9.1,8.7,9.2,9.4,7.6,8.2)
y <- c(25.5,31.2,25.9,38.4,18.4,26.7,26.4,25.9,32,25.2,39.7,35.7,26.5)
# stepwise selection
bothStep <- stepAIC(lm(y~x1+x2+x3), direction='both’)
# 결과 출력
summary(bothStep)

# backward elimination
backStep <- stepAIC(lm(y~x1+x2+x3), direction='backward’)
# 결과 출력
summary(backStep)

# forward selection을 사용하려면 절편만 포함하는 모형을 지정, 설명
변수는 scope으로 입력
# forward selection
forwardStep<-stepAIC(lm(y~1), direction='forward', scope=~x1+x2+x3)
# 결과 출력
summary(forwardStep)

3. 로지스틱회귀분석

1. 로지스틱회귀분석 (Logistic Regression)

• 회귀모텔에서 종속변수의 값의 형태가 연속형 숫자가 아닌 범주형 값인 경우를 다루기 위해서 만들어진 통계적 방법

• 예. iris 데이터셋에서4개의 측정값을 가지고 품종을 예측하는 모형을 구축할 때 사용하는 방법. (종속변수(품종)이 범주형 값)
  

• 범주형 응답변수에 사용된다는 점을 제외하면 선형 회귀와 유사

• 로지스틱 회귀분석은 두 개 이상의 클래스로 일반화 할 수 있음

• 변수 선택을 통해 유의미한 설명변수를 선택하여 최적의 모형을 찾을 수

• 활용 분아 : 머신러닝의 분류 모텔

  • 고객을 재구매 고객과 저음 구매한 고객으로 분류하기
  • 신용 점수와 같은 정보로부터 대출의 승인 또는 비승인 예측하기
    

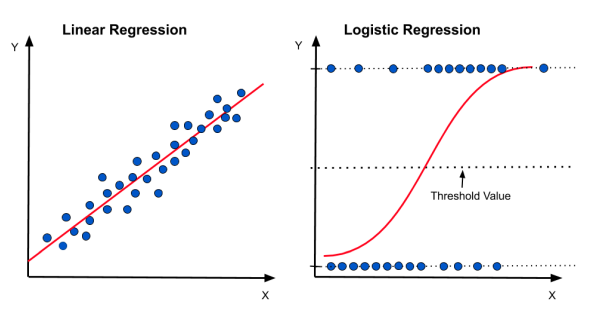
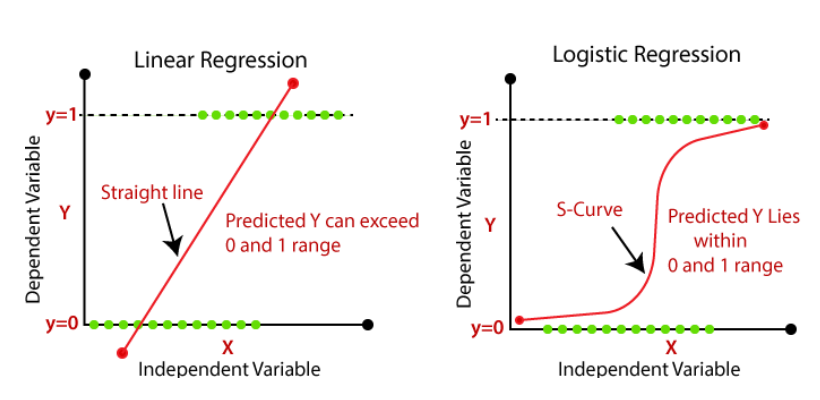
• 종속변수(Y)가 0 또는 1 (사망/생존, 성공/실패, 합격/불합격) 이면 선형 회귀로는모형fitting 할 수 없음 곡선으로fitting

• 곡선으로fitting하는 변환 : 로짓(logit)변환
  
  

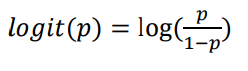
R예제

iris: Species(품종)과 Sepal.Length(꽃받침)의 관계성/예측

#data 생성 (종속변수가 2개의 카테고리를 갖도록)
iriS2 <- subset(iris, species==aversicolor")
# 종속변 수를 factor로 변형
iris2$Species <- factor(iris2$Species)
#로지스틱 회귀분석
modell 수 gIm(Species ~ SepaI.Length, data=iris2, family="binomial")
summary(modell)
#회귀계수
coef(modell)
#Sepal Length가 1 증가할수록 품종이 로짓 log(p/(l-p))가 5.14 증가
[p:목표변수가 더 큰 값(y=2, versicolor)을 가질 확률을 추정]
수 exponential을 취하면, 오즈(p/(1-p))가 e514배 증가

# 적합 결과
fitted(model1)
# 품종 예측
new <- data.frame(Sepal.Length = 3.8)
pred <- predict(model1, new, type=“response”)
pred
 1
0.0002489091
#Sepal.Length 값이 3.8을 갖는 경우는 Species(품종)이 versicolor (y=2)일
확률이 0.00024이다. → setosa
# 품종명 출력
pred <- round(pred,0)+1
levels(iris2$Species)[pred]