1. 노이즈

1.1노이즈 (Noise)

• 측정된 변수에 무작위의 오류(random error) 또는 분산(variance)이 존재하는 것

1.1.1 정형 데이터의 노이즈

• 정형 데이터에서 노이즈는 분산(variance)으로 나타남
  • 분산은 데이터의 무작위 변동을 의미
  • 이상치는 데이터의 무작위 변동을 초과하는 특정한 값으로 별도로 처리함
• 통계 모형에서는 오차항으로 나타남
  • 오차항은 모형에서 설명하지 못하는 무작위 변동을 의미
  • 예를 들어 단순선형회귀모형에서 오차항이 노이즈임

1.1.2 이미지/영상 데이터의 노이즈

• 이미지/영상에서 노이즈는 blur, white noise, pink noise, Gausian noise 등 다양한 형태로 나타남
  • blur : 이미지가 흐릿하게 보이는 현상
  • white noise : 백색 잡음, 모든 주파수를 가진 잡음
  • pink noise : 특정 주파수 대역(일반적으로 낮은 주파수)에서 강하게 나타나는 노이즈
  • Gausian noise : 가우시안 분포를 따르는 잡음
    • 정규 분포 노이즈는 자연 현상이나 전자 장비에서 발생하는 노이즈 중 가장 일반적인 형태
• 이미지/노이즈의 주요 원인은
  • 이미지 획득과정에서 너무 낮은 수집된 광자의 양, 센서/렌즈 열화(degradation) 등
  • 이미지 전송 중 무선 통신의 에코 및 대기 왜곡 등

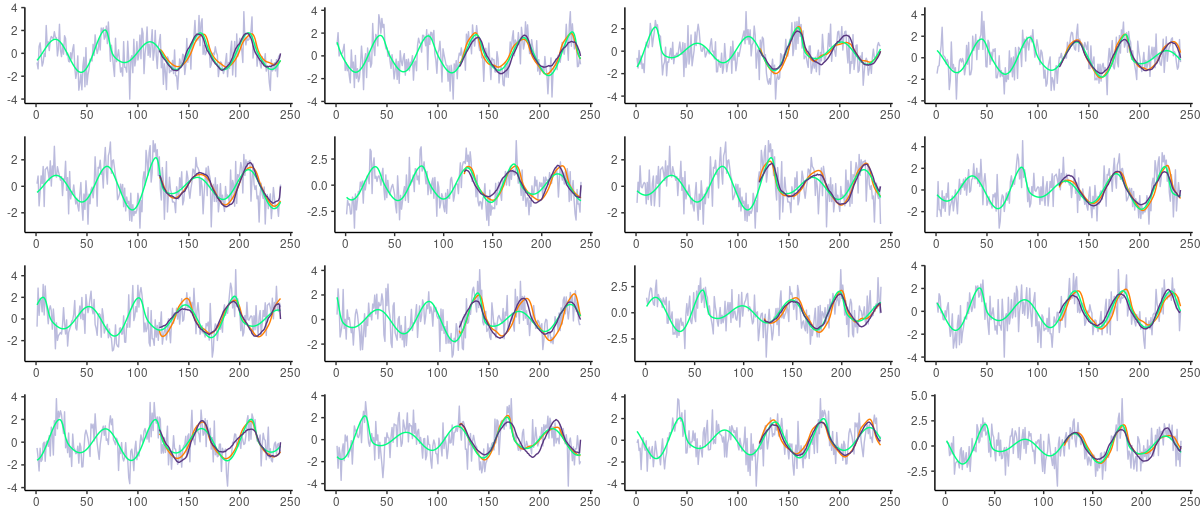
1.1.3 시계열/음성/신호 데이터의 노이즈

• 시계열/음성/신호에서 노이즈는 일반적으로 white noise(백색잡음) 또는 Gaussian noise(가우시안 잡음)으로 나타남
  • 백색잡음은 모든 주파수 영역에서 동일한 에너지를 가지는 잡음
  • 가우시안 잡음은 평균이 0이고 분산이 1인 정규분포를 따르는 잡음

1.1.4 텍스트 데이터의 노이즈

• 일반적으로 철자 오류, 약어, 비표준 단어, 반복, 구두점 누락, 대소 문자 정보 누락, “음” 및 “어”와 같은 의성어 등
• 텍스트 데이터의 노이즈는 자연어 처리의 성능을 저하시키는 중요한 요인
• 자동 음성 인식, 광학 문자 인식, 기계 번역, Web Scraping 등으로 수집한 데이터에 노이즈가 많음

---

음성 인식 예

“test data에 대해서도 1hat incoding을 해줍니다. 그다음에 이 부분이 저희가 모델을 만드는 부분이에요. 그래서 모델을 만드는데 이 Sequential이라는 KERAS에 있는 함수를 사용을 할 거고요 그래서 첫 번째 줄에 model sequnha을 하면 모델에 이런 sequnh한 model을 넣겠다. 근데 지금은 비어 있는 상태가 되고 여기서는 그냥 모델을 sqn셜한 모델로 생성을 한 거고요 여기에 저희가 implayer hidnaye 아웃플레이어를 add를 해주게 되면 됩니다. 그래서 첫 번째로 저희가 해주는 걸 보면 model add에서 여기서 inforter dense라는 layer를 넣어요.”

---

1.2 Defact(결함) vs. Fault(불량) vs. Artifact(아티팩트) vs. Noise(잡음, 노이즈)

• Defact, Fault, Artifact, Noise는 의미는 명확히 구분되나 혼재되어 사용됨

1. Defact(결함)

• Defact는 전체 데이터에 존재하는 일부 오류(error) 데이터
  • 범위에서 벗어난 이상치(outlier)가 아니라 잘못된(error) 데이터
  • 주로 생산이나 제조 분야에서 사용하는 용어(아래의 사진은 반도체 결함)
    • Defact가 제품/설비의 기능에 손상을 야기하면 제품/설비가 Fault(불량/기능이상)이 됨
    • 모든 defect가 fault를 야기하지는 않음

• Artifact(아티팩트)는 Defact와 동일한 의미를 갖는 용어
  • 주로 과학기술 분야에서 사용하는 용어, 특히, 이미지의 defect를 지칭

Noise(잡음, 노이즈)

• Noise는 일반적으로 그 원인을 알 수 없는 무작위 변동을 의미
  • 무작위(ramdom)가 발생하는 기전(mechanism)을 알 수 없다는 의미임
  • 발생 기전을 알게되면, random 중 수학적 모형을 통하여 반영된 것을 제외한 것이 random이 됨
• 주로 신호처리(signal processing) 분야에서 사용하는 용어임
• 데이터 과학에서는 데이터의 무작위 변동을 의미
• 동작 기전을 모르므로 제거는 불가하고 이를 저감(Denoising)하여야 함
  • 디노이징 기법은 기본적으로 평활화(smoothing, 구간평균), 구간화(binning, 구간집계), 필터링(filtering, 주파성분 저감)기법을 사용

---

디노이징(Denoising)

• 디노이징은 데이터에서 노이즈를 저감하여 모형이 더 좋은 성능을 할 수 있도록 하는 전처리 과정

2.1 정형 데이터의 디노이징

• 구간화(Binning)
  • 정렬된 데이터 값들을 몇 개의 bin(혹은 bucket)으로 분할하여 대표값으로 대체
• 군집화(clustering)
  • 유사한 값들을 하나의 군집으로 처리하여 중심점(centroid)을 대표값으로 대체

2.1.1 구간화(Binning)

구간설정 방법

1. 동일 간격(equal-distance) 구간화 → pandas의 cut() 사용

• 동일한 간격으로 구간을 설정
  • 정상 데이터가 한쪽으로 편중(biased)되고 outlier에 의해 영향을 많이 받음
  • 한쪽으로 몰려있는 데이터들은 다 동일한 bin으로 들어오기 때문에 skewed data를 다룰 수 없음

2. 동일 빈도(eual-frequency) 구간화 → pandas의 qcut() 사용

• 동일한 개수의 데이터를 가지는 구간으로 설정

구간별 대표값 설정 방법

• 평균값 평활화 : bin에 있는 값들을 평균값으로 대체
• 중앙값 평활화 : 중앙값으로 대체
• 경계값 평활화 : 경계값 중 가까운 값으로 대체

import pandas as pd
import numpy as np

라이브러리 불러오는 과정

# 데이터 생성하기, 결과를 보기 용이하도록 sort
df = pd.DataFrame({'uniform': np.sort(np.random.uniform(0,10,10)),
                     'normal': np.sort(np.random.normal(5,1,10)),
                     'gamma': np.sort(np.random.gamma(2, size=10))})

데이터 프레임 생성후에 3가지 열 생성. 10가지 랜덤값 제공

• np.random.uniform(0, 10, 10): 0부터 10까지의 균일 분포에서 10개의 랜덤 숫자를 생성
• np.random.normal(5, 1, 10): 평균이 5이고 표준편차가 1인 정규 분포에서 10개의 랜덤 숫자를 생성
• np.random.gamma(2, size=10): 형상 매개변수가 2인 감마 분포에서 10개의 랜덤 숫자를 생성

# 데이터 확인하기
df.plot(kind='hist', bins=15, alpha=0.5)
df.describe()

• df.plot(kind='hist', bins=15, alpha=0.5): 히스토그램을 그림.
  'kind' 매개변수는 'hist'로 설정되어 있어 히스토그램을 나타냅니다. 'bins'는 히스토그램의 막대 개수를 지정하고, 'alpha'는 투명도를 나타냅니다.

2.1.1.1 Pandas로 구간화

# cut(), qcut() 기본 동작 확인
col = 'uniform'
num_bins = 5
df_binned = pd.DataFrame()
df_binned[col] = df[col].sort_values()  # 원 데이터

'uniform' 열에서 데이터를 가져와 정렬한 후, 이를 df_binned라는 새로운 DataFrame에 'uniform' 열로 추가

df_binned['eq_dist_auto'] = pd.cut(df_binned[col], num_bins)  # 동일 간격으로 나누기

cut() 함수를 사용하여 데이터를 동일한 간격으로 나눠서 'eq_dist_auto' 열에 추가

cut() 함수는 연속형 데이터를 구간으로 나눌 때 사용, num_bins에 지정된 개수만큼의 동일한 간격으로 나눔

df_binned['eq_dist_fixed'] = pd.cut(df_binned[col], bins=[0,2,4,6,8,10]) 

cut() 함수를 다시 사용하여 지정된 구간으로 데이터를 나눔, bins 매개변수에는 사용자가 지정한 구간의 경계값을 리스트로 전달

# 지정된 구간으로 나누기
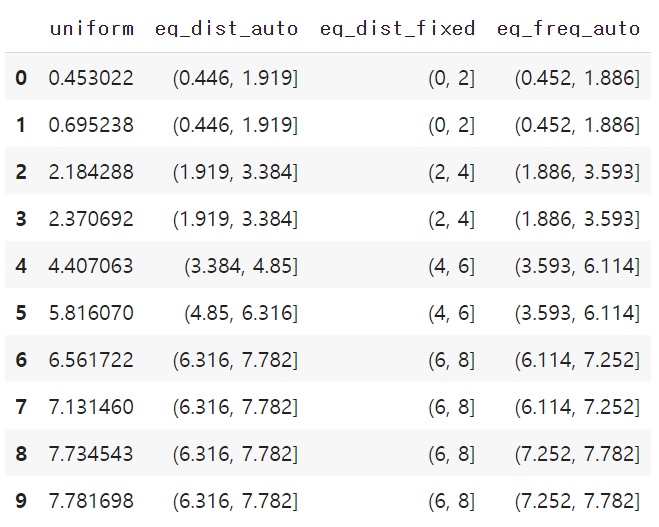
df_binned['eq_freq_auto'] = pd.qcut(df_binned[col], num_bins) # 동일 빈도로 나누기
df_binned

qcut() 함수를 사용하여 동일한 빈도로 데이터를 나누어 'eq_freq_auto' 열에 추가

qcut() 함수는 데이터의 분포를 기반으로 동일한 빈도로 나누어주는 함수
num_bins에 지정된 개수만큼 나눔

# 구간화하여 평균값 대체하기
cols = ['uniform', 'normal', 'gamma']

열들을 리스트로 정의

# 동일 간격 구간화
df_ew = df.copy()
for col in cols:
    df_ew[col+'_eq_dist'] = pd.cut(df_ew[col], 3)   # 구간으로 나누기
    means = df_ew.groupby(col+'_eq_dist')[col].mean() # 구간별 평균값 계산
    df_ew.replace({col+'_eq_dist': means}, inplace=True) # 평균값으로 대체

display(df_ew)

df_ew라는 새로운 데이터프레임을 생성

주어진 열들을 동일한 간격으로 구간화하여 해당 열의 이름에 '_eq_dist'를 추가한 새로운 열을 만듬

groupby를 사용하여 각 구간별로 해당 열의 평균값을 계산

replace를 사용하여 원본 데이터프레임에서 해당 구간을 그 구간의 평균값으로 대체

# 동일 빈도 구간화
df_ef = df.copy()
for col in cols:
    df_ef[col+'_eq_freq'] = pd.qcut(df_ef[col], 3)   # 구간으로 나누기
    means = df_ef.groupby(col+'_eq_freq')[col].mean() # 구간별 평균값 계산
    df_ef.replace({col+'_eq_freq': means}, inplace=True) # 평균값으로 대체

display(df_ef)

qcut() 함수를 사용하여 동일한 빈도로 구간화하고, 평균값을 계산하여 대체

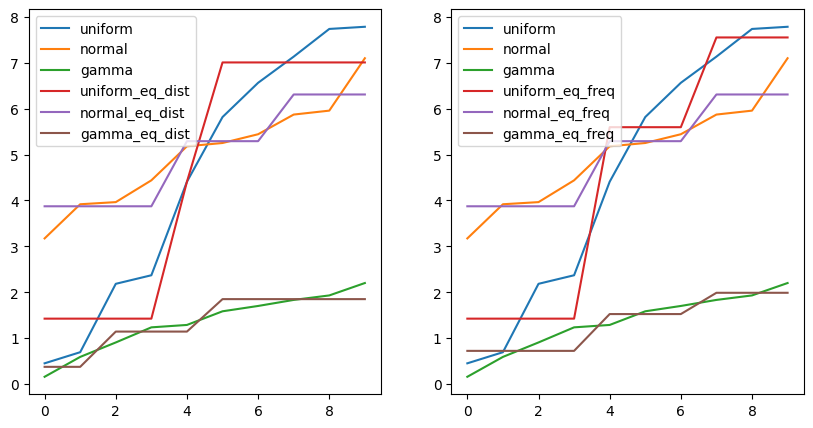
# 시각화
import matplotlib.pyplot as plt

fig, axes = plt.subplots(1, 2, figsize=(10,5))
df_ew.astype(float).plot(ax=axes[0])
df_ef.astype(float).plot(ax=axes[1])
plt.show()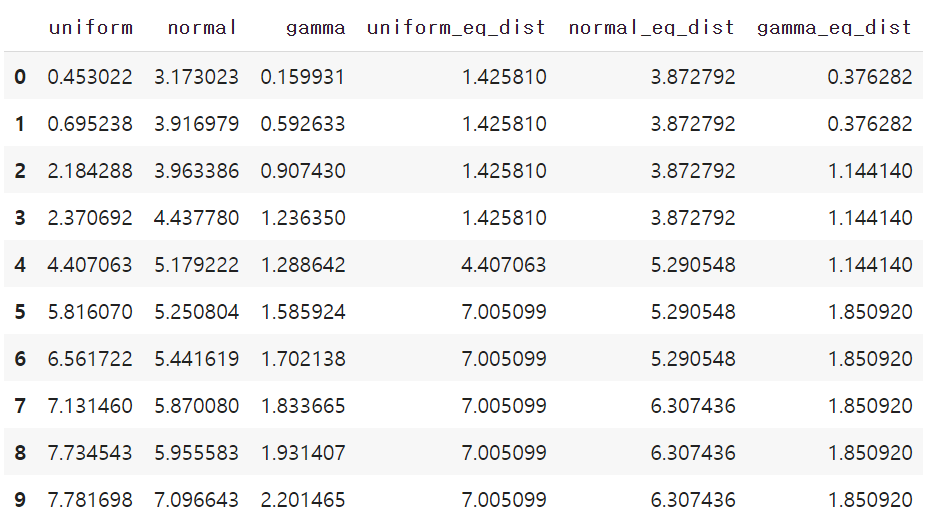

2.1.2 군집화(clustering)

2.1.2.1 Scikit-Learn으로 구간화

• KBinsDiscretizer() 사용
  • encode{‘onehot’, ‘onehot-dense’, ‘ordinal’}, default=’onehot’
  • strategy{‘uniform’(동일간격), ‘quantile’(동일빈도), ‘kmeans’(K-Means 군집화)}, default=’quantile’

import warnings

# hide warnings
warnings.filterwarnings("ignore")

from sklearn.preprocessing import KBinsDiscretizer

경고 메시지를 무시하기 위해 warnings 모듈을 사용

filterwarnings 함수로 모든 경고를 무시하도록 설정

sklearn.preprocessing 모듈에서 KBinsDiscretizer 클래스를 가져옴

연속형 데이터를 구간화하는 데 사용

# 동일 간격 구간화
ed_binner = KBinsDiscretizer(n_bins=3, encode='ordinal', strategy='uniform', subsample=None)
df_ed = ed_binner.fit_transform(df)

동일한 간격으로 구간화를 수행

KBinsDiscretizer 객체를 생성하고, fit_transform 메서드를 사용하여 주어진 데이터프레임 df를 동일한 간격으로 구간화

df_ed라는 새로운 배열로 저장

# 동일 빈도 구간화
ef_binner = KBinsDiscretizer(n_bins=3, encode='ordinal', strategy='quantile', subsample=None)
df_ef = ef_binner.fit_transform(df)

동일한 빈도로 구간화를 수행

KBinsDiscretizer 객체를 생성하고, fit_transform 메서드를 사용하여 주어진 데이터프레임 df를 동일한 빈도로 구간화

df_ef라는 새로운 배열로 저장

# K-means 구간화
km_binner = KBinsDiscretizer(n_bins=3, encode='ordinal', strategy='kmeans', subsample=None)
df_km = km_binner.fit_transform(df)

K-means 알고리즘을 기반으로 한 구간화를 수행

KBinsDiscretizer 객체를 생성하고, fit_transform 메서드를 사용하여 주어진 데이터프레임 df를 K-means 알고리즘을 사용하여 구간화

df_km라는 새로운 배열로 저장

# 결과 확인
df_ed = pd.DataFrame(df_ed, columns=df.columns+'_eq_dist')
df_ef = pd.DataFrame(df_ef, columns=df.columns+'_eq_freq')
df_km = pd.DataFrame(df_km, columns=df.columns+'_km')
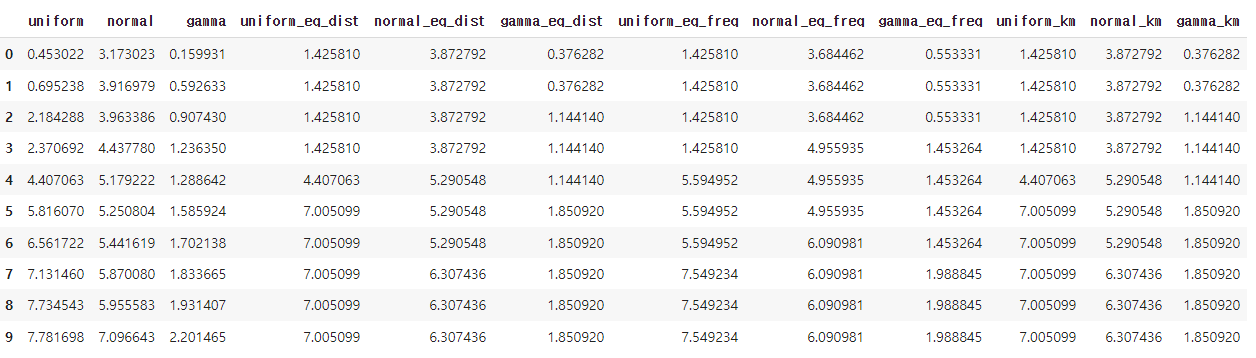
df_bin = pd.concat([df, df_ed, df_ef, df_km], axis=1)
df_bin

구간화된 결과를 데이터프레임으로 변환하고, 이를 기존의 데이터프레임 df와 합치는 작업을 수행

pd.concat 함수를 사용하여 각 구간화 결과를 새로운 열로 추가한 df_bin라는 새로운 데이터프레임을 생성

# 구간화하여 평균값 대체하기
for bin_col in df_bin.columns:
    col = bin_col.split('_')[0]
    

df_bin에 대해 각 구간 별로 해당 열의 평균값으로 대체하는 작업을 수행

df_bin의 각 열에 대해 반복문을 실행

bin_col은 현재 반복 중인 열을 나타남

해당 열의 이름에서 '_eq_dist', '_eq_freq', '_km'와 같은 부분을 제외하고 실제 열 이름을 가져옴

얻은 열 이름은 col에 저장

    means = df_bin.groupby(by=bin_col)[col].mean() # 구간별 평균값 계산
    

groupby 메서드를 사용하여 현재 반복 중인 열(bin_col)을 기준으로 그룹을 만듦

그룹에 속하는 해당 열의 값들의 평균을 계산

means 변수에 저장

    df_bin.replace({bin_col: means}, inplace=True) # 평균값으로 대체

df_bin

replace 메서드를 사용하여 원본 데이터프레임 df_bin에서 현재 반복 중인 열(bin_col)의 값을 means에 저장된 평균값으로 대체

inplace=True 옵션은 원본 데이터프레임을 직접 수정하도록 지정

# 시각화
import matplotlib.pyplot as plt

fig, axes = plt.subplots(1, 3, figsize=(15,5))
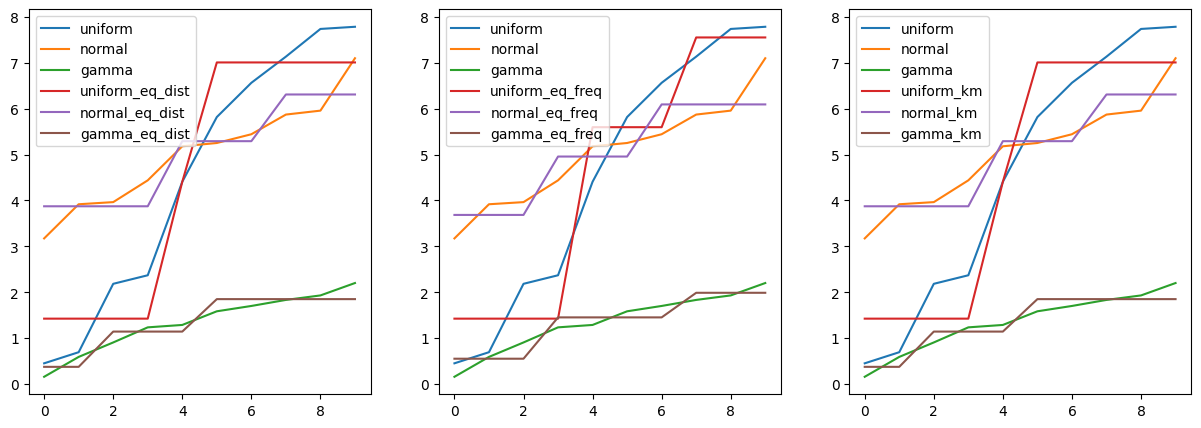
pd.concat([df_bin.iloc[:,:3], df_bin.iloc[:,3:6]], axis=1).astype(float).plot(ax=axes[0])
pd.concat([df_bin.iloc[:,:3], df_bin.iloc[:,6:9]], axis=1).astype(float).plot(ax=axes[1])
pd.concat([df_bin.iloc[:,:3], df_bin.iloc[:,9:]], axis=1).astype(float).plot(ax=axes[2])
plt.show()

matplotlib의 pyplot 모듈을 가져옴

1행 3열의 subplot을 가진 Figure 객체를 생성

각 subplot은 axes 변수에 저장

figsize 매개변수를 사용하여 전체 그림의 크기를 지정

subplot에 대해, 원본 데이터프레임에서 0부터 2열까지의 열과, 구간화된 데이터프레임에서 3부터 5열까지의 열을 선택하여 이를 하나의 데이터프레임으로 합친 후, astype(float)를 사용하여 모든 값을 실수형으로 변환한 뒤, plot 메서드를 사용하여 그림

그리고 이를 첫 번째 subplot (axes[0])에 플로팅

적용해보기

import pandas as pd
import numpy as np
from sklearn.preprocessing import KBinsDiscretizer

# 데이터 생성하기
np.random.seed(42)
data = pd.DataFrame({
    'feature1': np.random.rand(100) * 10,  # Uniformly distributed between 0 and 10
    'feature2': np.random.randn(100) * 2 + 5,  # Normally distributed with mean 5 and standard deviation 2
})

# 데이터 확인하기
data.plot(kind='scatter', x='feature1', y='feature2')
plt.title('Original Data')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

# 데이터 구간화 및 대체
features = ['feature1', 'feature2']
n_bins = 5

# KBinsDiscretizer를 사용하여 동일 간격으로 구간화
binner = KBinsDiscretizer(n_bins=n_bins, encode='ordinal', strategy='uniform')
data_binned = pd.DataFrame(binner.fit_transform(data[features]), columns=features)

# 각 구간의 중간값으로 대체
for feature in features:
    bin_col = feature + '_bin'
    bin_centers = binner.bin_edges_[features.index(feature)][:-1] + np.diff(binner.bin_edges_[features.index(feature)])/2
    data_binned[feature] = bin_centers[data_binned[feature].astype(int)]

# 시각화
data_binned.plot(kind='scatter', x='feature1', y='feature2')
plt.title('Binned and Replaced Data')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()