파이썬을 이용한 몬테카를로 예제에 관한 글입니다.

반복된 무작위 추출을 이용하여 함수의 값을 수리적으로 근사하는 알고리즘

동전 뒤집기

---

import random
import numpy as np
import matplotlib.pyplot as plt

# 동전 뒤집기 기능
def coin_flip():
    return random.randint(0,1) # 0과 1 중 무작위 추출
    
# 몬테 카를로

list = []

def monte_carlo(n):
    results = 0
    for i in range(n):
        flip_result = coin_flip() 
        results = results + flip_result 
        
        prob_value = results/(i+1) # 현재까지 앞면이 나온 횟수를 누적한 값에 대한 평균
        
        list.append(prob_value)
        
        plt.axhline(y=0.5, color='r', linestyle='-')
        plt.xlabel("Iteration")
        plt.ylabel("Probalility")
        plt.plot(list)
        
    return results/n
    
answer = monte_carlo(5000)
print("Final value :", answer)

파이값 추정

---

import turtle
import random
import matplotlib.pyplot as plt
import math

pen = turtle.Turtle()
pen.hideturtle()
pen.speed(0)

# 사각형
pen.up()
pen.setposition(-100,-100)
pen.down()
pen.fd(200)
pen.left(90)
pen.fd(200)

pen.left(90)
pen.fd(200)
pen.left(90)
pen.fd(200)
pen.left(90)

# 원
pen.up()
pen.setposition(0, -100)
pen.down()
pen.circle(100)

# 초기화
in_circle = 0
out_circle = 0

pi_values = []

for i in range(5):
    for j in range(10000):
        
        x = random.randrange(-100,100)
        y = random.randrange(-100,100)
        
        if (x**2+y**2>100**2):
            pen.color("black")
            pen.up()
            pen.goto(x,y)
            pen.down()
            pen.dot()
            out_circle = out_circle + 1
            
        else:
            pen.color("red")
            pen.up()
            pen.goto(x,y)
            pen.down()
            pen.dot()
            in_circle = in_circle+1
            
        pi = 4.0 * in_circle / (in_circle + out_circle)
        
        pi_values.append(pi)
        
        avg_pi_errors = [abs(math.pi - pi) for pi in pi_values]
        
    print (pi_values[-1])

시각화

plt.axhline(y=math.pi, color='g', linestyle='-')
plt.plot(pi_values)
plt.xlabel("Iterations")
plt.ylabel("Value of PI")
plt.show()

plt.axhline(y=0.0, color='g', linestyle='-')
plt.plot(avg_pi_errors)
plt.xlabel("Iterations")
plt.ylabel("Error")
plt.show()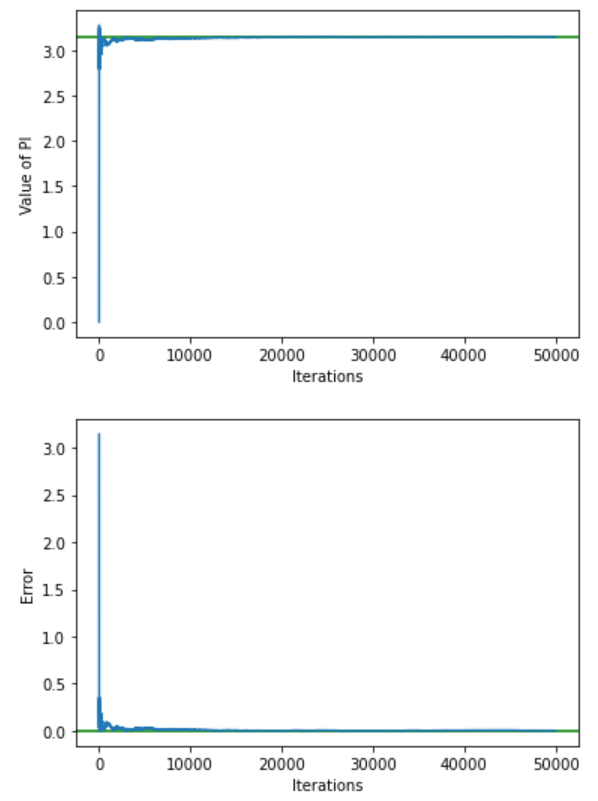

몬티홀 문제

---

세 개의 문 중 하나에 자동차가 있고 나머지 두 개에는 염소가 있습니다. 참가자는 처음에 문 하나를 선택하고, 진행자는 참가자가 선택한 문을 제외한 나머지 두 개 중 하나를 열어 염소를 보여줍니다. 그런 다음 참가자에게 선택을 바꿀 수 있는 기회가 주어집니다.

자동차가 아닌 문을 열었을 때 선택을 바꾸는 것이 유리

import random
import matplotlib.pyplot as plt

doors = ["goat", "goat", "car"]

#초기화
switch_win_probability = []
stick_win_probability = []

plt.axhline(y=0.66666, color='r', linestyle='-')
plt.axhline(y=0.33333, color='g', linestyle='-')

# 몬테카를로
def monte_carlo(n):
    
    switch_wins = 0
    stick_wins = 0
    
    for i in range(n):
        
        random.shuffle(doors)
        
        k = random.randrange(2)
        
        if doors[k] != 'car':
            switch_wins += 1
            
        else:
            stick_wins += 1
            
        switch_win_probability.append(switch_wins/(i+1))
        stick_win_probability.append(stick_wins/(i+1))
        
        plt.plot(switch_win_probability)
        plt.plot(stick_win_probability)
        
    print('Winning probability if you always switch:', switch_win_probability[-1])
    print('Winning probability if you always stick to your original choice:', stick_win_probability[-1])
    
monte_carlo(1000)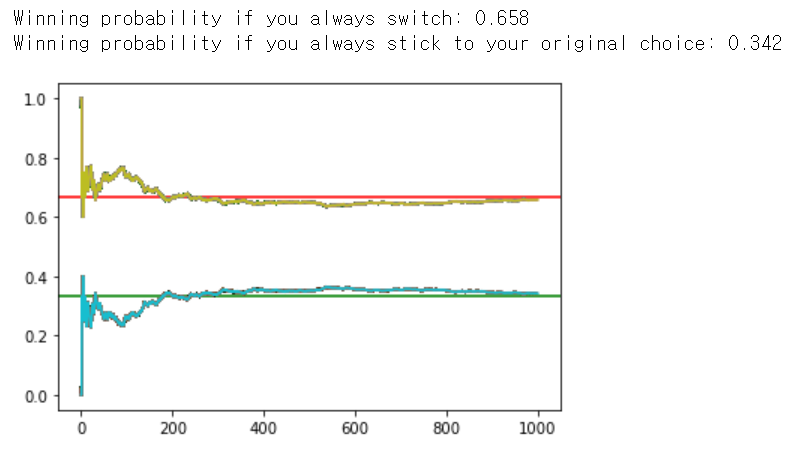

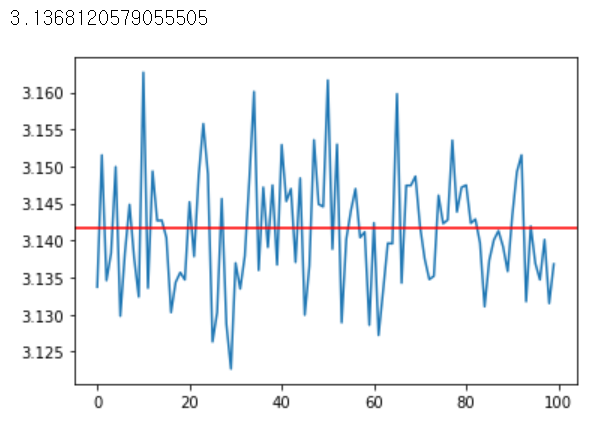
뷔퐁의 바늘 문제

---

바늘이 선 중 하나를 교차할 확률

이에 따른 원주율

import random
import math
import matplotlib.pyplot as plt

def monte_carlo(runs, needles, n_length, b_width):
    pi_values = []
    plt.axhline(y=math.pi, color='r', linestyle='-')

    for i in range(runs):
        nhits = 0 # 적중 바늘 수 초기화
        
        for j in range(needles):
            # 바늘이 선과 교차할 확률
            x = random.uniform(0, b_width/2.0)
            theta = random.uniform(0, math.pi/2)
            xtip = x - (n_length/2.0)*math.cos(theta)
            if xtip < 0:
                nhits += 1
                
        numerator = 2.0 * n_length * needles
        denominator = b_width * nhits
        
        pi_values.append((numerator/denominator))
        
    print(pi_values[-1])
    
    plt.plot(pi_values)
    
monte_carlo(100, 100000, 2, 2)