딥러닝 - Tensorflow: 선형회귀

1. 선형회귀 (Linear Regression)

• 주어진 입력 변수와 출력 변수 사이의 선형 관계를 모델링하는 기법

• 단순선형회귀의 경우, 다음과 같은 수식의 형태를 가짐

  $y = wx + b$, $(w$=가중치, $b$= 절편$)$

2. 딥러닝 기반 구현

• 손실 함수: 일반적으로 평균제곱오차(Mean Squared Error; MSE) 사용

  $\text{MSE} = \frac{1}{N} \sum_{i=1}^{N} (y_i - \hat{y}_i)^2$, $(y_i$=실제값, $\hat{y}_i$=예측값$)$

• 최적화 반복: 경사하강법(Gradient Descent)을 이용하여 손실을 최소화하는 방향을 찾고, 옵티마이저를 이용하여 $w$와 $b$를 업데이트

• 유의사항

  • $w$와 $b$의 초기값이 결과 수렴 속도에 영향을 미칠 수 있음
  • 학습률(learning_rate)이 너무 크면 발산하고, 너무 작으면 수렴 속도가 느릴 수 있음
  • 데이터 크기에 따라 적합한 반복 횟수(epoch)를 설정하여야 함

3. Tensorflow 코드 예제

• 가상 데이터셋 생성 및 시각화

import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import seaborn as sns
plt.rc("font", family="Liberation Sans")

import tensorflow as tf
tf.random.set_seed(777)

W_true = 3.0
b_true = 2.0
X = tf.random.normal([500, 1])
noise = tf.random.normal([500, 1])
y = X * W_true + b_true + noise

fig = plt.figure(figsize=(4, 3))
plt.scatter(X, y, c="w", alpha=.5, edgecolors="grey")
plt.title("Original Data")
plt.show()

• 경사하강법 기반 회귀계수 최적화

W = tf.Variable(5.0) # W_true = 3.0
b = tf.Variable(0.0) # b_true = 2.0
lr = 0.03

# 변화과정 기록용 리스트 생성
W_records = []
b_records = []
loss_records = []

# 최적화 과정을 100번 반복
for epoch in range(100):
    with tf.GradientTape() as tape:
        y_hat = W * X + b
        loss = tf.reduce_mean(tf.square(y_hat - y)) # MSE
        
    # Variable별 변화과정 기록
    W_records.append(W.numpy())
    b_records.append(b.numpy())
    loss_records.append(loss.numpy())
        
    # W, b의 기울기 계산    
    dw, db = tape.gradient(loss, [W, b])
    
    W.assign_sub(lr * dw) # W.assign(W - lr * dw)와 동일
    b.assign_sub(lr * db) # b.assign(b - lr * dw)와 동일

• 최적화 과정 확인

# 변화과정을 데이터프레임 형태로 저장
res = pd.DataFrame({
    "W": W_records,
    "b": b_records,
    "loss": loss_records
})

# head 확인
print(res.head())
#           W         b      loss
# 0  5.000000  0.000000  8.073974
# 1  4.895945  0.109825  7.331703
# 2  4.797212  0.213387  6.667764
# 3  4.703531  0.311045  6.073869
# 4  4.614645  0.403138  5.542607

# tail 확인 시 W_true와 b_true에 근사함을 확인 가능
print(res.tail())
#            W         b      loss
# 95  2.990326  1.928001  1.022950
# 96  2.989663  1.928452  1.022929
# 97  2.989035  1.928879  1.022910
# 98  2.988440  1.929282  1.022894
# 99  2.987875  1.929662  1.022879

• Epoch 진행에 따른 Loss 변화 시각화

fig = plt.figure(figsize=(7, 3))
sns.lineplot(x=res.index, y=res.loss, color="red")
plt.title("Loss")
plt.xlabel("Epoch")
plt.ylabel(None)
plt.show()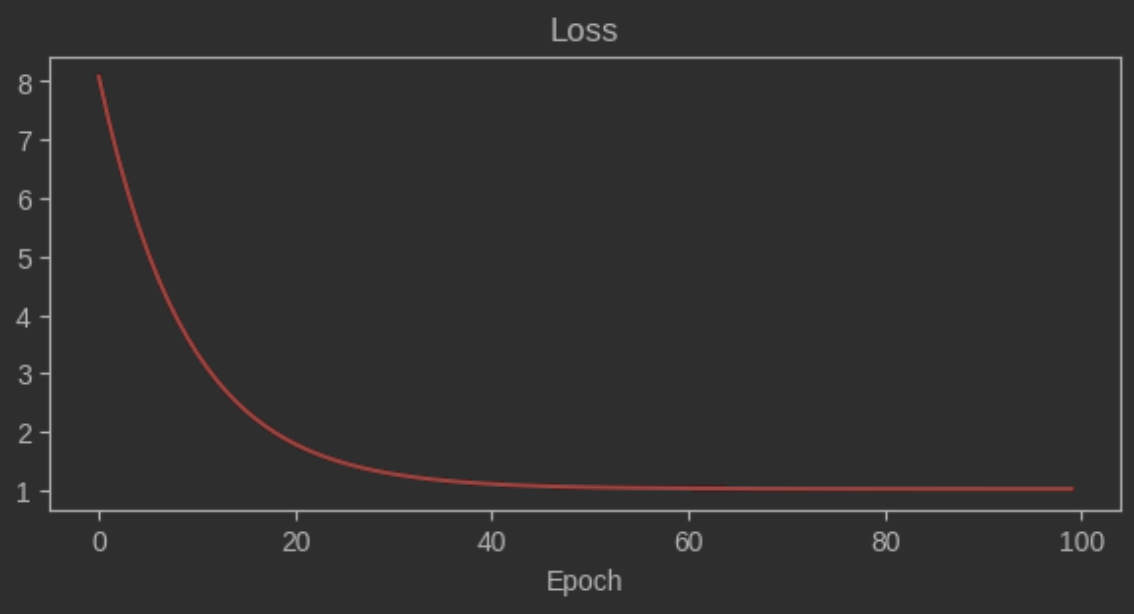

*이 글은 제로베이스 데이터 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다.