머신러닝 - 주성분 분석(PCA)

1.PCA(Principal Component Analysis; PCA) 개념

• 고차원 데이터를 저차원으로 축소하여 데이터의 주요 패턴을 파악하거나 시각화할 때 유용한 방법
• 기존 데이터의 분산을 최대로 설명할 수 있는 새로운 직교 좌표축(주성분)을 찾아 변환 실시
• 다음과 같은 효과를 보여줄 수 있음
  • 차원 축소: 고차원 데이터를 저차원으로 줄여 계산 효율성을 높임
  • 변수 선택: 중요하지 않은 변수(차원)를 제거하여 데이터의 주요 패턴만 보존
  • 시각화: 2D 또는 3D로 변환하여 고차원 데이터를 시각화할 수 있음

---

2. 계산 절차

2-1. 데이터 표준화

• 각 변수의 평균을 0으로 만드는 스케일링 과정을 적용

2-2. 공분산 행렬 계산

• 데이터의 공분산 행렬을 구해 각 변수 간 상관 관계를 계산

2-3. 고유값 분해

• 계산된 공분산 행렬을 고유값 분해하여 고유값과 고유벡터 도출
  • 고유값(Eigen Value): 각 주성분의 설명력(분산)을 나타냄
  • 고유벡터(Eigen Vector): 주성분의 방향을 나타냄

2-4. 주성분 선택 및 변환:

• 가장 큰 고유값에 대응하는 고유벡터를 선택하여 변환

---

3. 주성분 분석 구현

3-1. 가상 데이터 생성

• 상관관계가 존재하는 가상 데이터 생성

import numpy as np
import matplotlib.pyplot as plt

# 100개의 행과 세 개의 변수를 갖는 가상 데이터 생성
np.random.seed(42)
mean = [0, 0, 0] # 세 변수의 평균
cov = [[1, 0.8, 0.5], # 세 변수 간 상관관계
       [0.8, 1, 0.3],
       [0.5, 0.3, 1]]
data = np.random.multivariate_normal(mean, cov, size=100)
print(data[:5,:])
# [[-0.29024422 -0.65921211 -0.28787988]
#  [-1.53906451 -1.36364807 -0.82529455]
#  [-1.52344633 -0.93551024 -1.58104359]
#  [-0.71781502 -0.54383279  0.02041673]
#  [-1.02073437 -0.55533284  1.4033968 ]]

# 가상 데이터 시각화
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(data[:, 0], data[:, 1], data[:, 2], alpha=0.7, c="red")
ax.set_title("Before PCA")
ax.set_xlabel("Feature #1")
ax.set_ylabel("Feature #2")
ax.set_zlabel("Feature #3")
plt.show()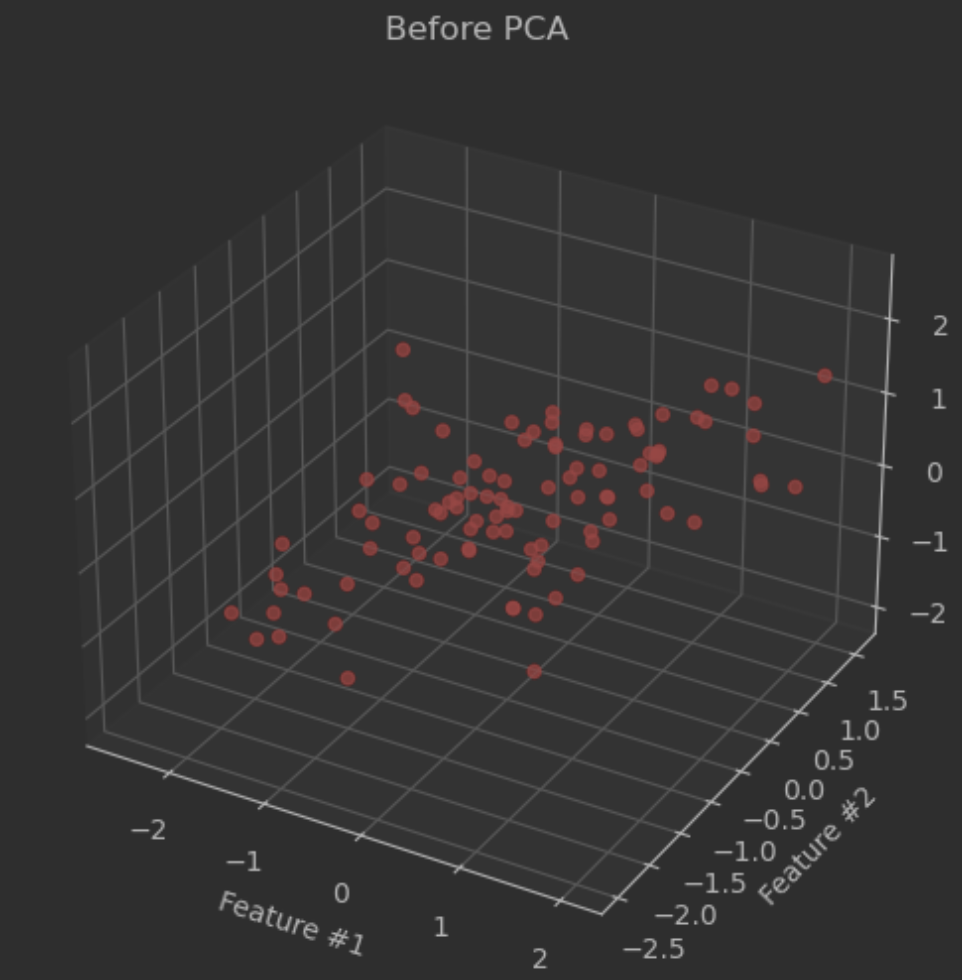

3-2. 데이터 표준화 및 공분산 행렬 계산

# 데이터 표준화
data_mean = np.mean(data, axis=0)
data_std = data - data_mean

# 공분산 행렬 계산
cov_matrix = np.cov(data_std.T)
print(cov_matrix)
# [[0.7998744  0.52631278 0.31789777]
#  [0.52631278 0.77345456 0.0685369 ]
#  [0.31789777 0.0685369  0.7666088 ]]

3-3. 고유값 분해

# 고유값 및 고유벡터 계산
eigen_val, eigen_vec = np.linalg.eig(cov_matrix)
print(eigen_val) # [1.43175444 0.20019827 0.70798505]
print(eigen_vec)
# [[ 0.69710943  0.71533245 -0.04835216]
#  [ 0.59844859 -0.61769053 -0.51021337]
#  [ 0.39483885 -0.32673827  0.85868759]]

# 고유값 정렬(내림차순)
idx = np.argsort(eigenvalues)[::-1]
eigenvalues = eigenvalues[idx]
eigenvectors = eigenvectors[:, idx]
print(eigen_val) # [1.43175444 0.70798505 0.20019827]
print(eigen_vec)
# [[ 0.69710943 -0.04835216  0.71533245]
#  [ 0.59844859 -0.51021337 -0.61769053]
#  [ 0.39483885  0.85868759 -0.32673827]]

3-4. 데이터 변환

# 두 개의 변수로 축소하기 위해 두 번째 고유벡터까지만 활용
# 원본 데이터와 행렬곱 실시
data_pca = data_std @ eigen_vec[:,:2]
print(data_pca.head())
# [[-0.56968609 -0.04838888]
#  [-2.07401139 -0.09006438]
#  [-2.10530441 -0.95821352]
#  [-0.67697365  0.1781475 ]
#  [-0.34896951  1.38620961]]

3-5. 결과 시각화

plt.figure(figsize=(12, 5))
plt.scatter(data_pca[:, 0], data_pca[:, 1], alpha=0.7, c="orange")
plt.title("After PCA")
plt.xlabel("Principal Component #1")
plt.ylabel("Principal Component #2")
plt.show()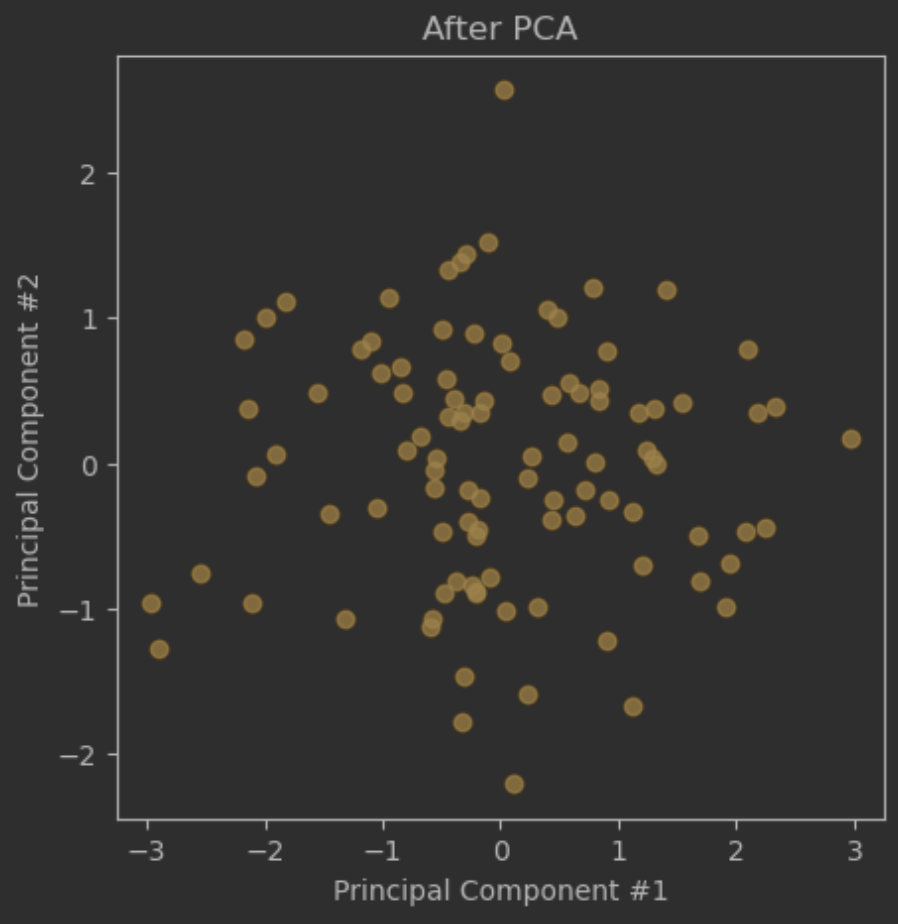

---

4. 예제 코드 (Scikit-learn)

4-1. 데이터 준비 및 시각화

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris

# 데이터 로드
iris = load_iris()
X = iris.data
y = iris.target

# 첫 세 개의 feature만 사용하여 산점도 시각화
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], alpha=0.7, c=y)
ax.set_title("Before PCA")
ax.set_xlabel("Feature #1")
ax.set_ylabel("Feature #2")
ax.set_zlabel("Feature #3")
plt.show()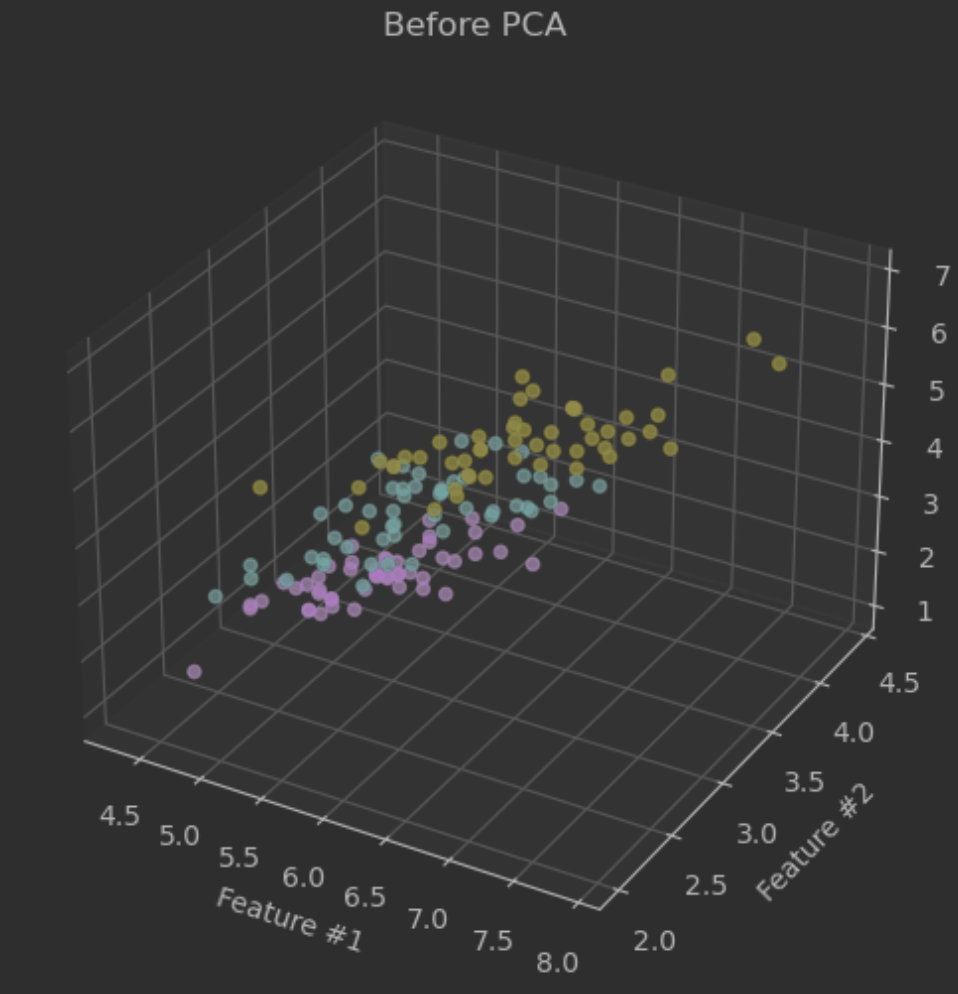

4-2. PCA 변환

from sklearn.decomposition import PCA

# PCA 객체 생성
pca = PCA(n_components=2) # 최대 2개의 주성분만 추출

# PCA 변환
X_pca = pca.fit_transform(X)

print("PCA 변환 전:", X.shape)
print("PCA 변환 후:", X_pca.shape)
# PCA 변환 전: (150, 4)
# PCA 변환 후: (150, 2)

4-3. 변환 결과 확인

plt.figure(figsize=(5, 5))
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, cmap='viridis', edgecolor='k')
plt.xlabel('Principal Component #1')
plt.ylabel('Principal Component #2')
plt.title('After PCA')
plt.show()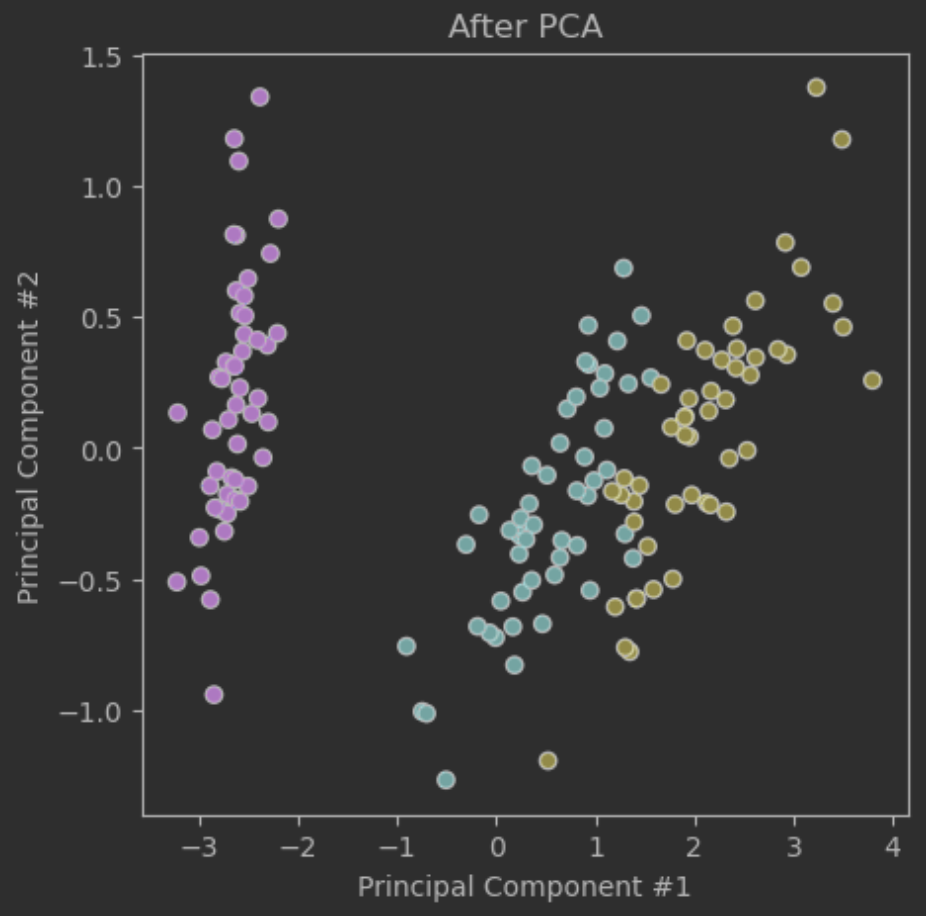

4-4. 주성분별 설명력 확인

print("주성분별 설명력", pca.explained_variance_ratio_)
print("총 설명력:", sum(pca.explained_variance_ratio_))
# 주성분별 설명력 [0.92461872 0.05306648]
# 총 설명력: 0.9776852063187962

---

*이 글은 제로베이스 데이터 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다.