머신러닝 - 군집 분석

dumbbelldore·2025년 1월 4일

ML dbscan k-means python 계층적군집 군집분석 데이터취업스쿨 비지도학습 제로베이스

zero-base 33기

목록 보기

60/97

1. 군집분석 (Cluster Analysis)

데이터를 유사성이 높은 그룹(Cluster)으로 묶는 기법
각 그룹 내 데이터는 가장 유사하도록, 그룹 간 데이터는 가장 상이하도록 분석과정이 진행됨
활용분야: 고객 세그먼테이션, 문서 분류, 이상치 탐지 등

2. 종류

2-1. K-Means 군집분석

사전에 정한 $k$ 개의 그룹으로 나누기 위한 초기 중심점 설정
각 데이터 포인트는 가장 유사한 그룹의 중심(centroid)에 가깝게 할당되며, 이를 기반으로 새로운 중심점을 계산하는 단계를 반복
원리가 간단하며 대규모 데이터에 적합하나, $k$ 의 올바른 설정이 성능을 크게 좌지우지 할 수 있음

2-2. DBSCAN (Density-Based Spatial Clustering of Applications with Noise)

데이터 밀도를 기준으로 그룹을 나눔. 즉, 밀도가 높은 곳은 그룹으로 인식되나 밀도가 낮은 곳은 그룹으로 인식되지 않음
밀도가 낮은 곳의 데이터 포인트로 이상치 탐지를 수행할 수 있으나, 밀도 관련 하이퍼파라미터의 올바른 설정이 중요함

2-3. 계층적 군집분석 (Hierarchical Clustering)

각 데이터 포인트를 병합해가며 그룹을 확장해가는 '병합형(Agglomerative)'과, 하나의 그룹에서 시작하여 그룹을 분할해가는 '분할형(Divisive)' 기법이 존재
클러스터 개수를 사전에 지정할 필요가 없고, 덴드로그램을 활용해 클러스터 간 관계를 시각화할 수 있으나 대규모 데이터에 적합하지 않음

3. 예제 코드

분석을 위한 가상 데이터셋 생성

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs

# 3개의 군집을 이루는 500개의 데이터
data, grp = make_blobs(n_samples=500, centers=3, cluster_std=3, random_state=42)

print(data.shape) # (500, 2)

# 시각화
plt.figure(figsize=(5,5))
plt.scatter(data[:,0], data[:,1], c=grp, alpha=.7)
plt.title("Generated Data")
plt.show()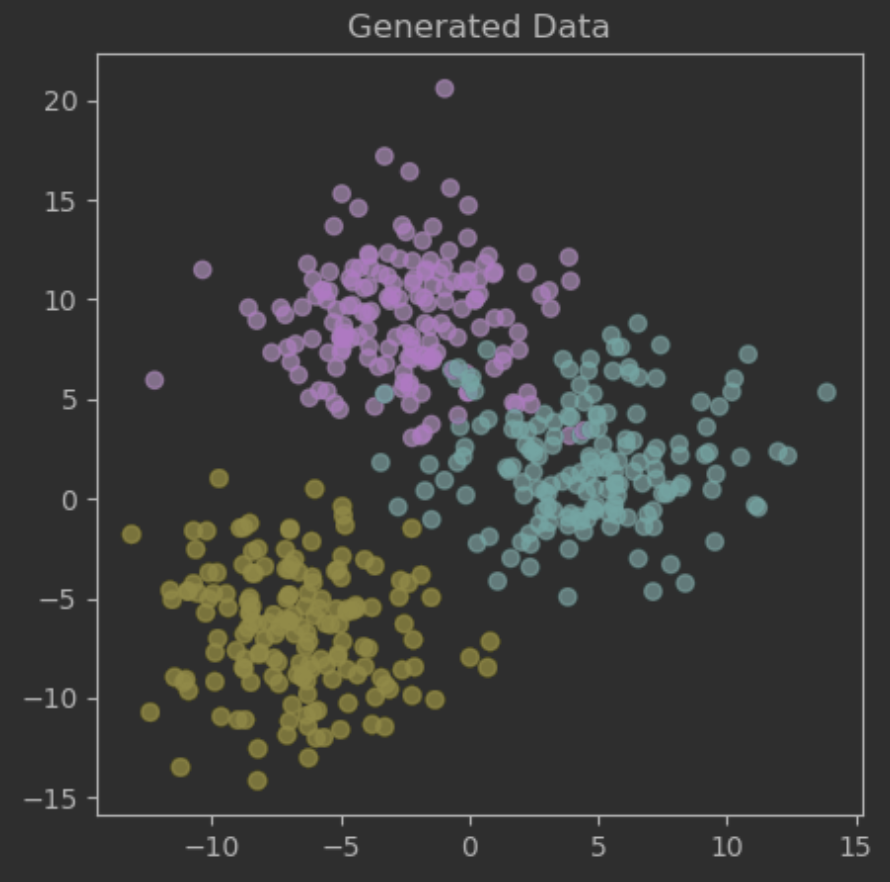

3-1. K-Means

$\text{SSE(Inertia)}$ 기준 최적 $k$ 값 탐색
- $\text{SSE(Inertia)}=\sum^{n}_{i=1}\min_{c_{k}}||x_{i}-\mu_{k}||^{2}$
- 즉, 각 그룹 내 데이터 포인트가 중심점에서 얼마나 가까운지를 측정한 지표로 작을수록 유리

from sklearn.cluster import KMeans

k_list = np.arange(2, 7, 1)
inertia_list = list()

for k in range(2,6):
    km = KMeans(n_clusters=k, random_state=42)
    grp_km = km.fit_predict(data)
    inertia_list.append(km.inertia_)

print("최소 SSE 보유 k 값:", k_list[np.argmin(inertia_list)])
# 최소 SSE 보유 k 값: 5

최적 $k$ 값 기준 모델 생성 및 시각화

km = KMeans(n_clusters=5, random_state=42)
grp_km = km.fit_predict(data)

plt.figure(figsize=(5,5))
plt.scatter(data[:,0], data[:,1], c=grp_km, alpha=.7)
plt.title("K-Means (k=5)")
plt.show()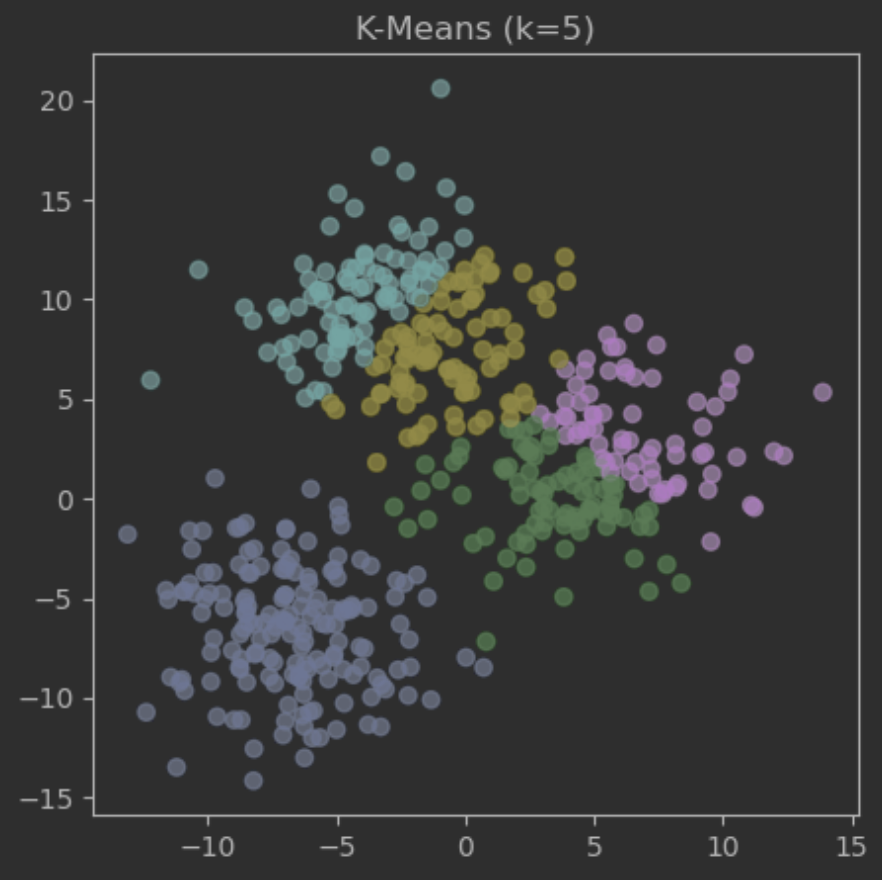

3-2. DBSCAN

실루엣 점수 기반 최적 $\epsilon$ , $\text{min\_samples}$ 설정
- $\epsilon$ : 하나의 데이터 포인트로부터 $\epsilon$ 의 거리 내 존재하는 데이터 포인트는 $\text{min\_samples}$ 조건만 만족한다면 같은 그룹으로 간주, 통상적으로 0.1~1.0 사이 설정
- $\text{min\_samples}$ : 하나의 그룹을 형성시키기 위해 모여야 하는 최소한의 데이터 포인트 수, 통상적으로 3~10 사이 설정
- 실루엣 점수 (Silhouette Score): $s=\frac{b-a}{max(a,b)}$ ( $a$ =응집도, $b$ =분리도)와 같이 나타낼 수 있으며, 각 데이터 포인트마다 계산되므로 통상적으로 평균함으로써 군집 성능을 판단
  - 1에 가까운 경우: 해당 데이터 포인트는 군집화가 완벽히 이루어졌음
  - 0에 가까운 경우: 해당 데이터 포인트는 두 그룹의 경계에 존재
  - -1에 가까운 경우: 해당 데이터 포인트는 군집화가 잘못 이루어졌음 (정 반대의 그룹에 존재)

from sklearn.cluster import DBSCAN
from sklearn.metrics import silhouette_score

# 해당 데이터 샘플은 0.1~1.0 범위 내 탐색 시 성능 저하로 탐색 범위 확대
epsilon_list = np.arange(0.1, 3.0, 0.1)
min_samples_list = np.arange(3, 10, 1)
result = list()

# 수동 Grid Search 실시
for epsilon in epsilon_list:
    for min_samples in min_samples_list:
        
        dbs = DBSCAN(eps=epsilon, min_samples=min_samples)
        grp_dbs = dbs.fit_predict(data)
        
        if len(np.unique(grp_dbs)) == 1: 
            continue # 실루엣 계수는 최소 2개의 그룹이 존재해야 계산 가능
        
        sil = silhouette_score(data, grp_dbs)
        result.append([epsilon, min_samples, sil])

# Grid Search 결과 데이터프레임 생성
res = pd.DataFrame(result, columns=['epsilon', 'min_samples', 'sil']).\
    sort_values(by="sil", ascending=False)
print(res.head())

## 출력 결과
#      epsilon  min_samples       sil
# 117      2.1            4  0.486884
# 118      2.1            5  0.483196
# 110      2.0            4  0.480973
# 119      2.1            6  0.478070
# 136      2.3            9  0.473304

최적 $\epsilon$ , $\text{min\_samples}$ 기준 모델 생성 및 시각화

from sklearn.cluster import DBSCAN
db = DBSCAN(min_samples=4, eps=2.1)
grp_dbs = db.fit_predict(data)

# 분홍색 점(그룹값: -1)을 이상치로 탐지하는 방식으로도 활용 가능
plt.figure(figsize=(5,5))
plt.scatter(data[:,0], data[:,1], c=grp_dbs, alpha=.7)
plt.title("DBSCAN (eps=2.1, min_samples=4)")
plt.show()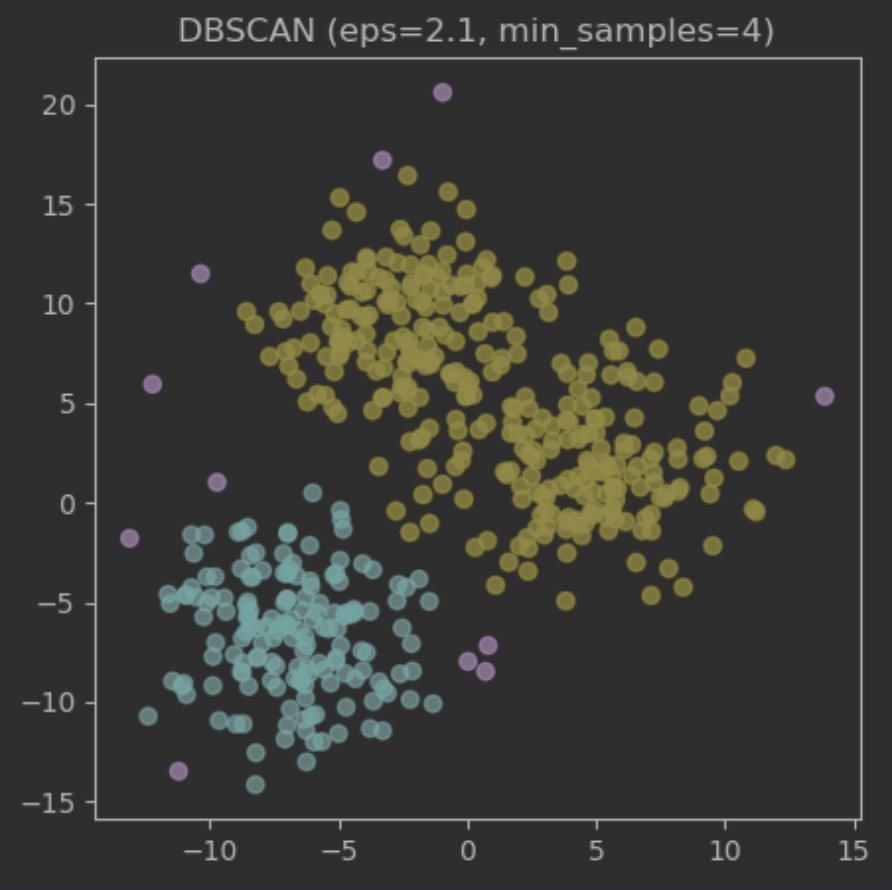

3-3. 병합형 계층적 군집분석

실루엣 계수 기반 최적 $\text{n\_clusters}$ 도출

from sklearn.cluster import AgglomerativeClustering

n_clusters_list = np.arange(2, 10, 1)
sil_list = list()

for n_clusters in n_clusters_list:
    agc = AgglomerativeClustering(n_clusters=n_clusters)
    grp_agc = agc.fit_predict(data)
    sil = silhouette_score(data, grp_agc)
    sil_list.append(sil)

print("최적 n_clusters 값:", n_clusters_list[np.argmax(sil_list)])
print(f"최고 실루엣 계수 값: {np.max(sil_list):.3f}")
# 최적 n_clusters 값: 3
# 최고 실루엣 계수 값: 0.536

최적 $\text{n\_clusters}$ 기반 모델링 및 시각화

agc = AgglomerativeClustering(n_clusters=3)
grp_agc = agc.fit_predict(data)  # 기본 "Euclidean" 거리, "ward" 연결법 사용

plt.figure(figsize=(5,5))
plt.scatter(data[:,0], data[:,1], c=grp_agc, alpha=.7)
plt.title("Agg. H-Clustering (n_clusters=2)")
plt.show()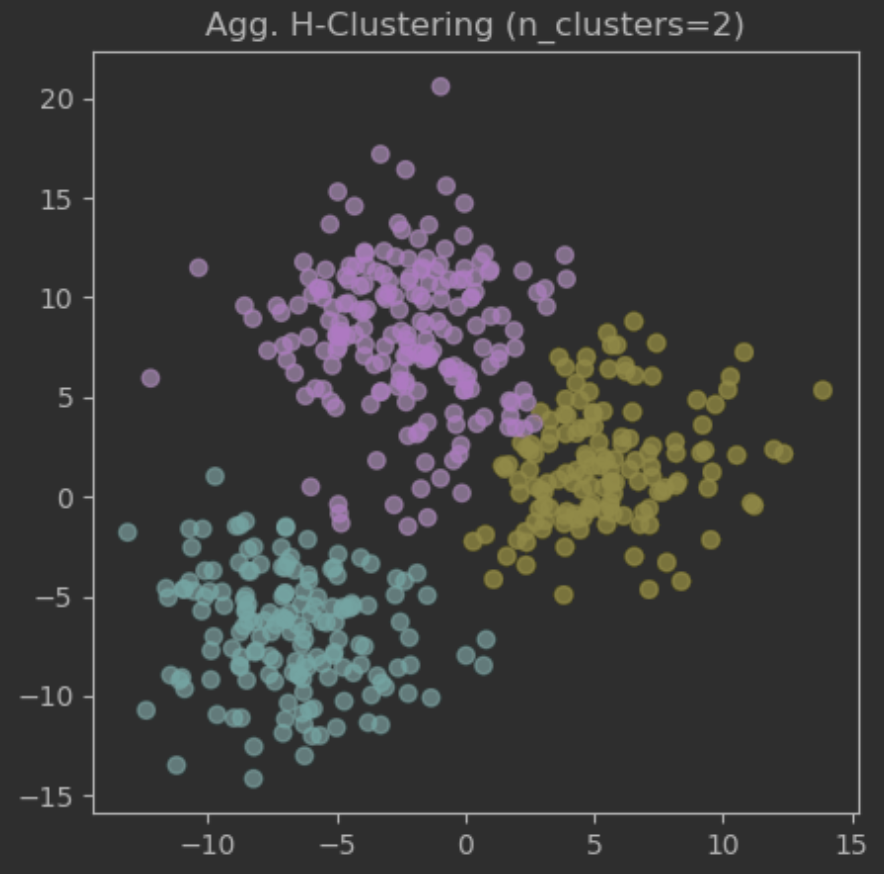

덴드로그램 시각화

from scipy.cluster.hierarchy import dendrogram, linkage

Z = linkage(data, method="ward")
plt.figure(figsize=(12,5))

# color_threshold는 덴드로그램을 그려가며 적절하게 조절 필요
dendrogram(Z, color_threshold=100, above_threshold_color="grey")

plt.title("Dendrogram")
plt.xticks([])
plt.show()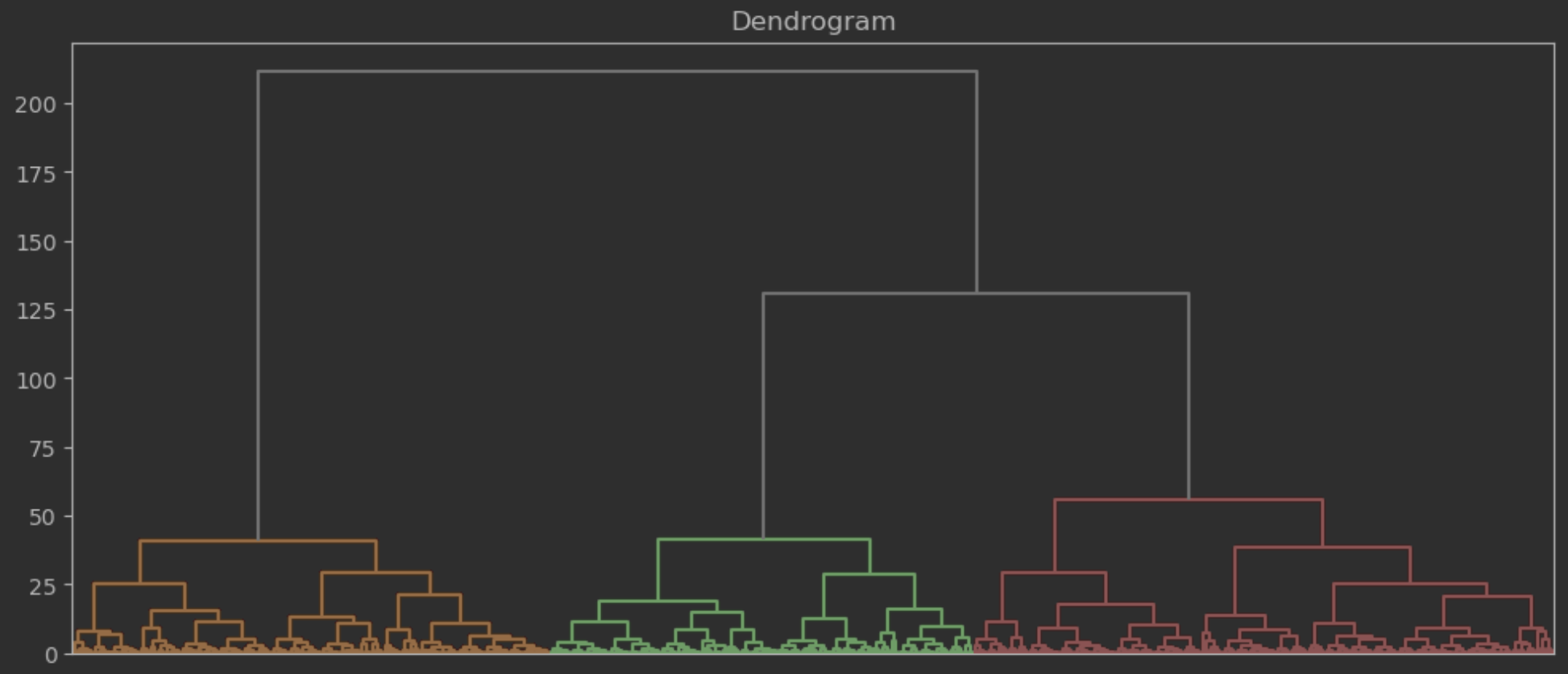

3-4. 분할형 계층적 군집분석

Scikit-learn에서는 분할형 계층적 군집분석을 지원하지 않으므로, K-Means 알고리즘과 while문을 사용하여 간이 사용자 정의 함수를 제작할 수 있음

from sklearn.cluster import KMeans

def DivisiveClustering(data, k):
    
    # 그룹별로 리스트에 담음
    grps = [data]
    
    # 원하는 k개의 그룹이 만들어질 떄까지 반복
    while len(grps) < k:
        # 가장 큰 그룹을 두 하위 그룹으로 분할
        tgt_grp_idx = np.argmax([len(grp) for grp in grps])
        tgt_grp = grps.pop(tgt_grp_idx)
        km = KMeans(n_clusters=2, random_state=42)
        grp_km = km.fit_predict(tgt_grp)
        
        # 분할된 두 그룹을 리스트에 다시 추가
        grps.append(tgt_grp[grp_km == 0])
        grps.append(tgt_grp[grp_km == 1])
    
    # 리스트 내 각 그룹별 데이터가 다시 리스트로 담겨있는 형태로 반환
    return grps

# 분할형 군집분석 실시
grp_dvc = DivisiveClustering(data, 3)

# 그룹 정보를 담은 데이터프레임 생성
res = pd.DataFrame(columns=["col1", "col2", "grp"])
for idx, grp in enumerate(grp_dvc):
    df = pd.DataFrame(grp, columns=["col1", "col2"])
    df["grp"] = idx
    res = pd.concat([res, df], axis=0).reset_index(drop=True)

print(res.shape) # (500, 3)

print(res.head())
#         col1      col2 grp
# 0  -3.431807 -8.989639   0
# 1   0.800626 -7.168289   0
# 2  -8.754083 -6.801836   0
# 3 -10.247793 -5.732880   0
# 4  -6.632775 -3.683668   0

print(res.tail())
#          col1       col2 grp
# 495 -3.899451   7.617097   2
# 496 -1.478343   3.725166   2
# 497 -5.233270   4.777375   2
# 498 -2.316358   5.781052   2
# 499 -2.740503  10.037742   2
    
# 시각화
plt.figure(figsize=(5,5))
plt.scatter(res.iloc[:,0], res.iloc[:,1], c=res.grp, alpha=.7)
plt.title("Div. H-Clustering (k=3)")
plt.show()