머신러닝 - 평가 지표

1. 평가 지표 선정

• 평가지표 선정에 정해진 답은 없으나, 직면한 데이터의 특성과 분석기법의 목적 등을 고려하여 프로젝트 초기에 선정하여야 함
• 여러 지표를 함께 활용해 다각적으로 평가하면 모델의 성능을 더 면밀히 이해할 수 있음

1-1. 데이터의 불균형 상태 고려

• 클래스 불균형 상태의 데이터에는 정확도(Accuracy)의 사용의 유의미하지 않을 수 있음
• 정밀도(Precision), 재현율(Recall), F1-Score 사용에 대한 고려가 필요함

1-2. 모델링 목적 고려

• False Negative를 더 줄여야 하는 경우 : 재현율(Recall) 우선
  ex) 질병 탐지 (병에 걸리지 않았다고 분류한 환자의 비율 감소 중요)
• False Positive를 더 줄여야 하는 경우: 정밀도(Precision) 우선
  ex) 스팸메일 탐지 (스팸으로 분류한 정상 메일의 비율 감소 중요)
• False Positive, False Negative 모두 고려가 필요한 경우: F1-Score 활용
  ex) 채무불이행 탐지 (타이트한 예측은 수익 감소에 영향, 완화한 예측 기준은 부실채권 증가에 영향)

1-3. 지표의 특성 고려

• MSE는 더 큰 오류에 패널티를 부여할 수 있지만, 측정단위가 동일하지 않음
• MAE는 측정단위가 동일하여 해석이 단순함
• R²는 모델의 설명력을 직관적으로 나타내기에 적합함

1-4. 모델의 특성 고려

• 연속형 데이터에 대한 예측은 MSE, MAE 등의 지표 사용
• 확률 기반 분류 모델은 ROC-AUC, 임계값 기반 분류 모델은 정밀도(Preicison), 재현율(Recall) 사용

---

2. 회귀 모델의 평가 지표

2-1. MSE (Mean Squared Error)

• $\text{MSE} = \frac{1}{n} \sum_{i=1}^n (y_i - \hat{y}_i)^2$

   from sklearn.metrics import mean_squared_error

   y_true = [3, -0.5, 2, 7]
   y_pred = [2.5, 0.0, 2, 8]
   mse = mean_squared_error(y_true, y_pred)
   print(mse)  # 출력: 0.375

2-2. RMSE (Root Mean Squared Error)

• MSE의 제곱근을 씌운 형태, 측정단위가 독립변수와 동일해지므로 해석이 편리함

2-3. MAE (Mean Absolute Error)

• 평균 절대 오차: $\text{MAE} = \frac{1}{n} \sum_{i=1}^n |y_i - \hat{y}_i|$

  from sklearn.metrics import mean_absolute_error

  mae = mean_absolute_error(y_true, y_pred)
  print(mae)  # 출력: 0.5

2-4. R² (결정 계수)

• 모델의 설명력 정도를 나타내며, 값이 1에 가까울수록 예측이 정확함을 의미

from sklearn.metrics import r2_score

r2 = r2_score(y_true, y_pred)
print(r2)  # 출력: 0.9486

---

3. 분류 모델의 평가 지표 (이진분류 기준)

• 분류 모델의 평가 지표 계산 시, 모델의 예측결과에 대한 '정오분류표(Confusion Matrix)'가 활용됨

  	실제 Positive	실제 Negative
  예측 Positive	True Positive (TP)	False Positive (FP)
  예측 Negative	False Negative (FN)	True Negative (TN)

3-1. 정확도 (Accuracy)

• 전체 예측 중에서 맞게 예측한 비율

  $\text{Accuracy} = \frac{\text{TP} + \text{TN}}{\text{TP} + \text{FP} + \text{FN} + \text{TN}}$

• 예시:

  from sklearn.metrics import accuracy_score
  
  y_true = [1, 0, 1, 1, 0, 1, 0]
  y_pred = [1, 0, 1, 1, 0, 0, 1]
  acc = accuracy_score(y_true, y_pred)
  print(acc)  # 출력: 0.714

3-2. 정밀도 (Precision)

• Positive로 예측한 것 중 실제로도 Positive인 비율

  $\text{Precision} = \frac{\text{TP}}{\text{TP} + \text{FP}}$

• 예시:

  from sklearn.metrics import precision_score
  
  prec = precision_score(y_true, y_pred)
  print(prec)  # 출력: 0.75

3-3. 재현율 (Recall)

• 실제 Positive인 것 중 알맞게 Positive로 예측한 비율

  $\text{Recall} = \frac{\text{TP}}{\text{TP} + \text{FN}}$

• 예시:

  from sklearn.metrics import recall_score
  
  rec = recall_score(y_true, y_pred)
  print(rec)  # 출력: 0.6

3-4. F1-Score

• 정밀도와 재현율의 조화 평균을 나타내며, 불균형 데이터에서 적합함

  $F1 = 2 \cdot \frac{\text{Precision} \cdot \text{Recall}}{\text{Precision} + \text{Recall}}$

• 예시:

  from sklearn.metrics import f1_score
  
  f1 = f1_score(y_true, y_pred)
  print(f1)  # 출력: 0.6667

3-5. ROC-AUC (Receiver Operating Characteristic - Area Under Curve)

• ROC는 분류기의 임계값 변화에 따른 TPR(재현율)과 FPR(거짓양성률)을 시각화한 곡선을 칭함

  $\text{TPR} = \frac{\text{TP}}{\text{TP} + \text{FN}}, \quad \text{FPR} = \frac{\text{FP}}{\text{FP} + \text{TN}}$

• AUC는 ROC 아래의 면적을 말하며, 1에 가까울수록 분류 성능이 우수함을 의미 (0.5의 경우 아무 분별력이 없는 랜덤 추측 모델에 해당)

• ROC 곡선 그리는 법

  • 이진 분류 문제에서 모델 예측 확률값과 실제 라벨이 다음과 같다고 가정한다면,

    Index	실제 라벨	예측 확률
    1	1	0.9
    2	0	0.8
    3	1	0.7
    4	0	0.6
    5	1	0.55
    6	0	0.4

  • 각 예측 확률을 임계값으로 하여 TPR과 FPR 계산

    Threshold	TP	FP	TN	FN	TPR	FPR
    1.0	0	0	3	3	0.00	0.00
    0.9	1	0	3	2	0.33	0.00
    0.8	1	1	2	2	0.33	0.33
    0.7	2	1	2	1	0.67	0.33
    0.6	2	2	1	1	0.67	0.67
    0.55	3	2	1	0	1.00	0.67
    0.4	3	3	0	0	1.00	1.00

  • 각 임계값에서 계산된 FPR과 TPR의 점을 각각 X좌표, Y좌표에 찍어 연결

    

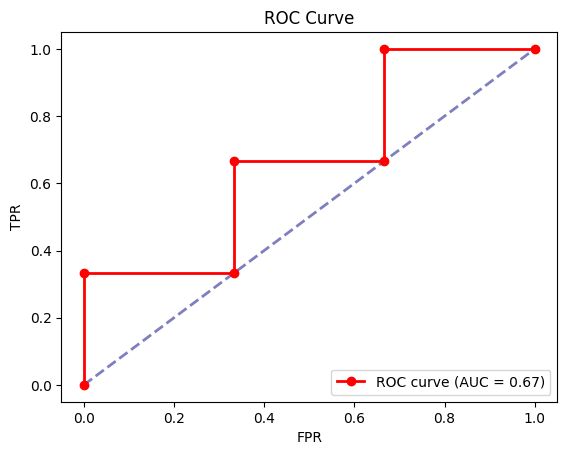
• 예시:

    import matplotlib.pyplot as plt
    from sklearn.metrics import roc_curve, auc
  
    # 예시 데이터 생성
    y_true = [1, 0, 1, 0, 1, 0] # 정답
    y_scores = [0.9, 0.8, 0.7, 0.6, 0.55, 0.4] # 모델 예측결과
  
    # ROC 요소 및 AUC 계산
    fpr, tpr, thresholds = roc_curve(y_true, y_scores)
    roc_auc = auc(fpr, tpr)
  
    # 시각화
    plt.figure()
    plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--', alpha=0.5)
    plt.plot(fpr, tpr, color='red', marker="o", lw=2, label=f'ROC curve (AUC = {roc_auc:.2f})')
    plt.xlabel('FPR')
    plt.ylabel('TPR')
    plt.title('ROC Curve')
    plt.legend(loc="lower right")
    plt.show()

---

*이 글은 제로베이스 데이터 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다.