https://darkpgmr.tistory.com/32
https://eehoeskrap.tistory.com/511
https://blog.daum.net/geoscience/1665

다음 블로그를 참고하여 정리하였다.
.
.
.

Camera Calibration 개념

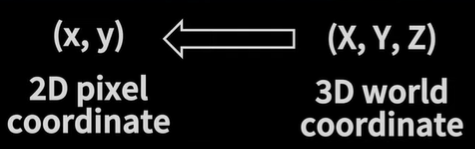
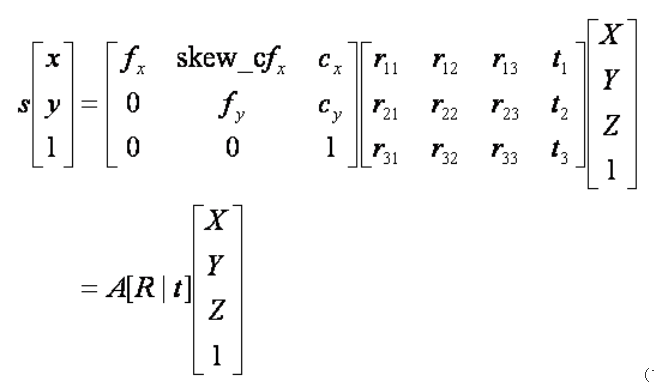
실제 세계는 3D이지만, 사진에서는 2D로 표현된다.
이때 3D 상의 점들이 2D에서는 어디에 대응되는지 기하학적으로 생각하면, 영상을 찍을 때의 카메라의 위치, 카메라의 방향 등 외부적인 요인의 영향을 받는다.
하지만, 뿐만 아니라 실제 이미지는 사용된 렌즈, 렌즈와 이미지 센서와의 거리, 렌즈와 이미지 센서가 이루는 각 등 내부적인 요인의 영향 또한 받게 되는데
3D 위치 좌표는 영상에 투영된 위치를 구하거나 or 역으로 영상 좌표로부터 3D를 복원할 때 위와 같은 내부 요인들을 제거해야 정확한 계산이 가능해진다.

이러한 내부적인 요인의 parameter값을 구하는 과정을
카메라 캘러브레이션(Camera Calibration)이라고 한다

사진이나 비디오를 촬영하는 실제 카메라 모델을 단순화시킨 핀홀(Pinhole) 카메라 모델의 매개변수를 추정하는 작업

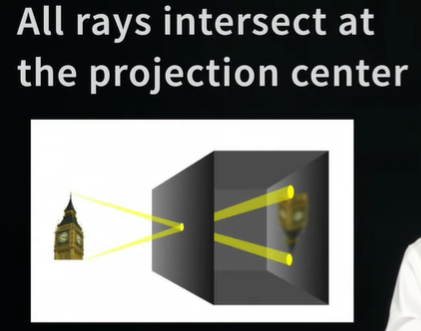
핀홀 카메라 모델이란?
: 하나의 바늘 구멍(pinhole)을 통해 외부의 상이 이미지로 투영되는 모델
: 바늘 구멍(pinhole)이 렌즈 중심, 이곳에서 뒷면의 상이 맺히는 곳까지의 거리 = 초점거리
: 핀홀 카메라의 매개변수는 카메라 행렬(Camera Matrix)라 불리는 3x4행렬로 표현
=> 이 매개변수를 추정하는 것이 바로 카메라 캘리브레이션

좌표의 종류

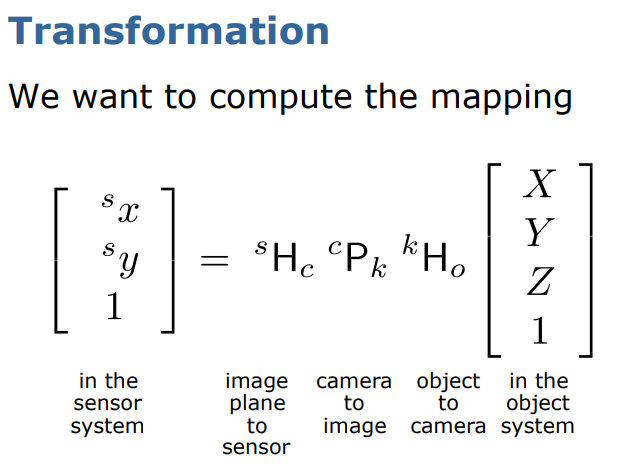
순서는 world->camera->image plane->sensor로!

카메라 모델의 매개변수

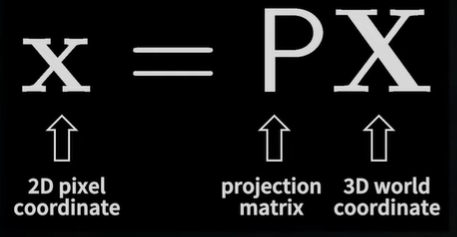
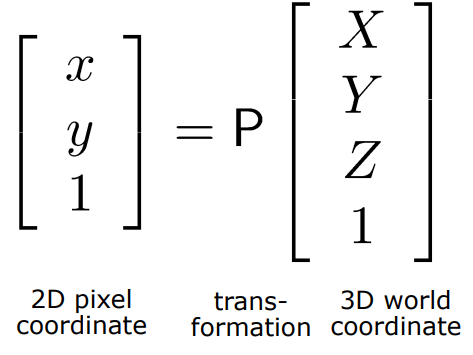
핀홀 카메라 모델에서 카메라 행렬(Camera Matrix)은

월드 좌표(world coordinate)에서 픽셀 좌표로 투영 매핑(projective mapping)을 나타내기 위해 사용됨

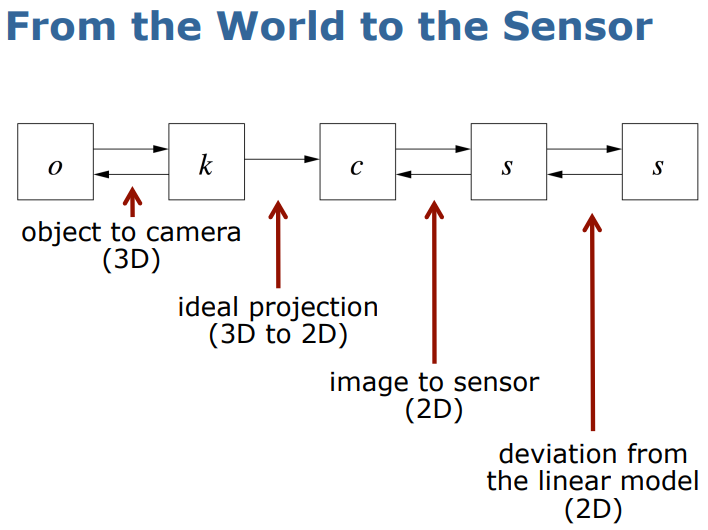
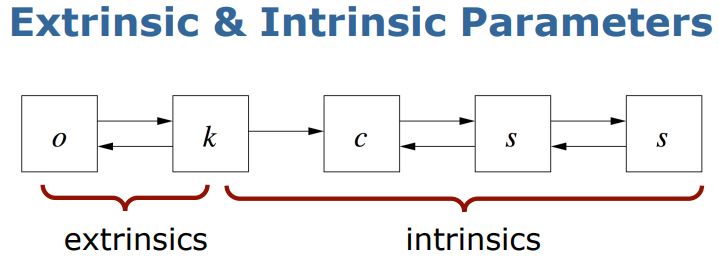
외부 매개변수(Extrinsic parameters)

카메라의 설치 높이, 방향 등 카메라와 외부공간과의 기하학적 관계에 관련된 파라미터

카메라 고유의 파라미터가 아니기 때문에 카메라를 어떤 위치에 어떤 방향으로 설치했는지에 따라 달라지고, 또한 월드 좌표계를 어떻게 정의했느냐에 따라 달라짐

카메라 좌표계와 월드 좌표계 사이의 변환관계를 설명하는 파라미터
두 좌표계 사이의 회전(rotation) 및 평행이동(translation) 변환으로 표현됨

카메라 외부 파라미터를 구하기 위해서는 먼저 캘리브레이션 툴 등을 이용하여 카메라 고유의 내부 파라미터들을 구합니다. 다음으로는 미리 알고 있는 또는 샘플로 뽑은 3D월드좌표–2D영상좌표 매칭 쌍들을 이용하여 식(1)에서 변환행렬을 구하면 됩니다.

내부 매개변수(Intrinsic parameters)

카메라의 초점 거리, aspect ratio, 중심점 등 카메라 자체의 내부적인 파라미터

• 5개의 내부 매개변수
• 초점거리(focal length), 이미지 센서 포맷(image sensor format), 주점(principal point)
  

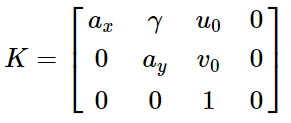
초점거리 (focus length)

: 렌즈 중심과 이미지센서(CCD,CMOS 등)와의 거리
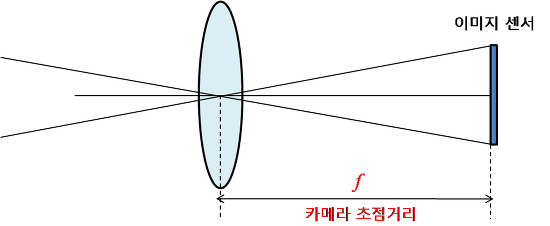디지털 카메라 등에서 초점거리는 mm단위로 표현되지만,
카메라 모델에서 말하는 초점거리(f)는 픽셀(pixel) 단위로 표현

1. $a_x = f * m_x$와 $a_y = f * m_y$는 픽셀단위의 초점 거리

• $m_x$와 $m_y$는 거리와 픽셀의 관계와 관련된 스케일 계수(scale factor)
• $f$는 거리단위의 초점거리

주점 (principal point)

: 카메라 렌즈의 중심, 핀홀에서 이미지 센서에 내린 수선의 발의 영상좌표
: 영상기하학에서 단순한 이미지 센터보다는 주점이 훨씬 중요하며, 영상의 모든 기하학적 해석은 이 주점을 이용하여 이루어짐

2. $u_0$와 $v_0$은 주점(principal point), 이상적인 경우 이미지의 중심이 주점

비대칭 계수(skew coefficient)

: 이미지 센서의 cell array의 y축이 기울어진 정도

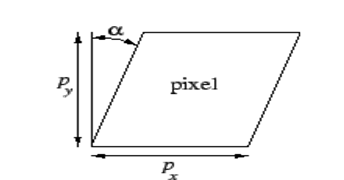
: 요즘 카메라들은 이러한 skew 에러가 거의 없기 때문에 카메라 모델에서 보통 비대칭 계수까지는 고려하지 않는다고 한다.

3. $\gamma$는 $x$과 $y$축 사이의 뒤틀림계수(skew coefficient), 종종 0이 된다