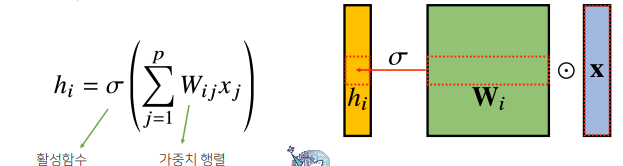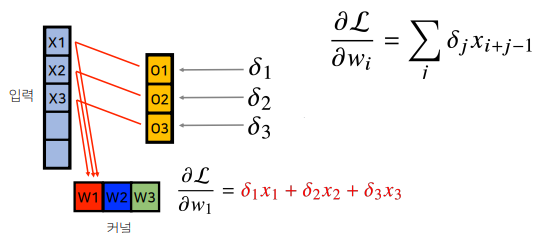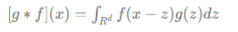[U stage DAY 5] AI Math (3)

먼지감자·2021년 8월 6일

boostcamp

AI Boostcamp 2기

목록 보기

5/48

강의 내용 복습

8강. 베이즈 통계학 맛보기

베이즈 정리

베이즈 정리는 조건부확률을 이용하여 정보를 갱신하는 방법을 알려준다.
A라는 새로운 정보가 주어졌을 때 p(B)로부터 P(B|A)를 계산하는 방법을 제공한다.

\begin{gathered} P(A \cap B)=P(B) P(A \mid B) \\ P(B \mid A)=\frac{P(A \cap B)}{P(A)}=P(B) \frac{P(A \mid B)}{P(A)} \end{gathered}

베이즈 정리를 활용한 예제.
COVID-99 의 발병률이 $10 \%$ 로 알려져있다. COVID-99 에 실제로 걸렸을 때 검진될 확률은 $99 \%$ , 실제로 걸리지 않았을 때 오검진될 확률이 $1 \%$ 라고 할 때, 어떤 사람이 질병에 걸렸다고 검진결과가 나왔을 때 정말로 COVID-99 에 감염되었을 확률은?

P(\theta \mid \mathcal{D})=P(\theta) \frac{P(\mathcal{D} \mid \theta)}{P(\mathcal{D})}

$P(\theta \mid \mathcal{D})$ : 사후확률 (데이터를 관찰한 이후에 hypothesis가 성립할 확률)
$P(\theta)$ : 사전확률 (데이터를 관찰하지 않은 상태에서 사전에 알려진 정보)
${P(\mathcal{D} \mid \theta)}$ : 가능도(likelihood) (모수가 주어진 상황에서 데이터 D가 관찰될 확률)
$P(\mathcal{D})$ : Evidence (데이터)

즉 사전확률, 민감도(Recall), 오탐율(False Alarm)을 가지고 정밀도 (Precision)을 계산하는 문제

\begin{array}{rl} P(\theta)=0.1 & P(\mathcal{D} \mid \theta)=0.99 \\ & P(\mathcal{D} \mid \neg \theta)=0.01 \end{array} \\ P(\mathcal{D})=\sum_{\theta} P(\mathcal{D} \mid \theta) P(\theta)=0.99 \times 0.1+0.01 \times 0.9=0.108 \\ P(\theta \mid \mathcal{D})=0.1 \times \frac{0.99}{0.108} \approx 0.916

0.916의 높은 정밀도를 확인할 수 있는데, 이는 잘못 판단할 확률이 0.01로 굉장히 작기 때문이다. 오검진될 확률(1종 오류)이 10%라면 결과는 달라진다.

\begin{array}{rl} P(\theta)=0.1 & P(\mathcal{D} \mid \theta)=0.99 \\ & P(\mathcal{D} \mid \neg \theta)=0.1 \end{array} \\ \begin{gathered} P(\mathcal{D})=\sum_{\theta} P(\mathcal{D} \mid \theta) P(\theta)=0.99 \times 0.1+0.1 \times 0.9=0.189 \\ P(\theta \mid \mathcal{D})=0.1 \times \frac{0.99}{0.189} \approx 0.524 \end{gathered}

위의 결과에서 확인할 수 있는것 처럼, 오탐율(False rate)이 오르면 테스트의 정밀도(Precision)가 떨어진다.

위의 예시에서 본 조건부 확률을 confusion matrix로 시각화하면
목적에 따라 다르지만 주로 1종 오류보다는 2종 오류가 클 경우 더욱 심각한 문제가 발생하므로 이 경우 FP를 희생하더라도 FN을 줄이는 형식으로 설계한다.

베이즈 정리를 통한 정보의 갱신

베이즈 정리를 통해 새로운 데이터가 들어왔을 때 앞서 계산한 사후확률을 사전확률로 사용하여 갱신된 사후확률을 계산할 수 있다.

앞서 COVID-99 판정을 받은 사람이 두 번재 검진을 받았을 때도 양성이 나왔을 떄 진짜 COVID-99에 걸렸을 확률은?

\begin{array}{r} P(\theta \mid \mathcal{D})=0.1 \times \frac{0.99}{0.189} \approx 0.524 \quad \begin{array}{c} P(\mathcal{D} \mid \theta)=0.99 \\ P(\mathcal{D} \mid \neg \theta)=0.1 \end{array} \\ P\left(\mathcal{D}^{*}\right)=0.99 \times 0.524+0.1 \times 0.476 \approx 0.566 \\ _{\text {갱신된 사후확률 }} P\left(\theta \mid \mathcal{D}^{*}\right)=0.524 \times \frac{0.99}{\text { (posterior) }}=0.917 \end{array}

인과관계 추론

인과관계는 데이터 분포의 변화에 강건한 예측모형을 만들 때 사용한다. 이 때, 조건부 확률을 함부로 인과관계(causality)추론에 사용해서는 안된다. 그 예로 심슨의 역설이라는 것이 있다.

두가지 치료법 a,b에 따른 병의 완치율간의 관계를 알고자
1. 단순 조건부 확률 (Overall)
2. 신장 결석 크기가 다른 환자에 따른 결과
를 확인해봤다.

단순히 조건부 확률로 각 치료법을 사용했을 떄의 완치율을 보면 치료법 b가 더 좋아보이지만, 신장의 크기가 다른 환자 각각을 보면 치료법 a의 결과가 더 좋은 것을 확인할 수 있다.
이는 신장 결석 크기 라는 조건이 치료법과 완치율에 연관되어 있는 중첩요인(confounding factor)로 작용했기 때문이다.

조정(intervention) 효과를 통해 중첩요인 Z의 개입을 제거하면 조건부 확률과는 반대의 결과가 나온다.

\begin{aligned} P^{\mathfrak{E}_{a}}(R=1) &=\sum_{z \in\{0,1\}} P^{\mathfrak{E}}(R=1 \mid T=a, Z=z) P^{\mathbb{C}}(Z=z) \\ \begin{array}{r} \end{array} &=\frac{81}{87} \times \frac{(87+270)}{700}+\frac{192}{263} \times \frac{(263+80)}{700} \approx 0.8325 \end{aligned} \\ \begin{aligned} P^{\mathfrak{G}_{b}}(R=1) &=\sum_{z \in\{0,1\}} P^{\mathfrak{C}}(R=1 \mid T=b, Z=z) P^{\mathbb{C}}(Z=z) \\ &=\frac{234}{270} \times \frac{(87+270)}{700}+\frac{55}{80} \times \frac{(263+80)}{700} \approx 0.7789 \end{aligned}

따라서 데이터 분석을 할 때 강건한 모델을 만들기 위해서는 단순 조건부 확률만 고려하지 말고, 데이터가 어떻게 만들어졌는지, 데이터 간의 상관관계가 있는지 등을 고려해야한다.

9강. CNN 첫걸음

CNN은 Convolutional neural network의 약자로, 모델 내에서 convolution 연산을 사용하여 특징을 뽑아낸다.

convolution 연산은 커널(kernel)을 입력벡터 상에서 움직여가면서 선형모델(convoltion 연산도 선형변환임)과 합성함수(활성화 함수)가 적용되는 구조이다. 이는 fully connected 구조와는 달리 모든 i에 대해 적용되는 가중치(커널)이 같아 파라미터 개수가 크게 줄어드는 효과가 있다.

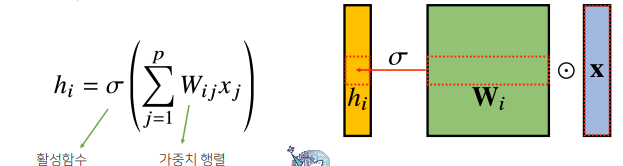
(위: fully connected layer) i가 바뀌면 사용되는 가중치도 바뀜
(아래: convolution layer) 모든 i에 대해 적용되는 가중치가 같음

해당 연산의 수학적 의미는 신호(signal)을 커널을 이용하여 국소적으로 증폭 또는 감소시켜 정보를 추출 또는 필터링 하는 것이다.

\begin{aligned} &\text { continuous }[f * g](x)=\int_{\mathbb{R}^{d}} f(z) g(x-z) \mathrm{d} z=\int_{\mathbb{R}^{d}} f(x-z) g(z) \mathrm{d} z=[g * f](x) \\ &\text { discrete } \quad[f * g](i)=\sum_{a \in \mathbb{Z}^{d}} f(a) g(i-a)=\sum_{a \in \mathbb{Z}^{d}} f(i-a) g(a)=[g * f](i) \end{aligned}

CNN에서 사용하는 연산은 위의 수식에서 뺴는 것이 아니라 더하기를 하기 때문에 convoution이 아니고 cross-correlation이라고 부름

convoution 연산은 1차원 뿐 아니라 다양한 차원에서도 가능한데 , 이를 수식으로 이해하기엔 쉽지 않아 2차원 convolution 을 그림으로 이해하면 다음과 같다.

2D convolution을 진행한 후 출력의 크기는 다음과 같으며, 출력 텐서의 채널수는 커널의 갯수와 같다.

\begin{aligned} &O_{H}=H-K_{H}+1 \\ &O_{W}=W-K_{W}+1 \end{aligned}

convolution 연산의 역전파

convolution 연산은 커널이 모든 입력 데이터에 대해 공통으로 적용되기 때문에 역전파를 계산할 때도 convolution 연산이 나오게 된다.
이 역시 그림으로 이해하면 다음과 같다.

1) 커널을 이동시키며 convolution 연산을 수행

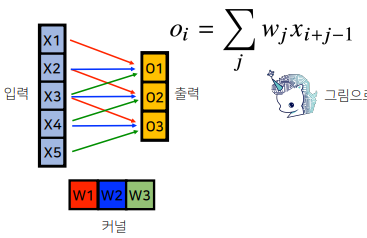
2) 하나의 입력 X3만 보면 다음과 같음, back propagation 시 미분값이 각 output으로 전달됨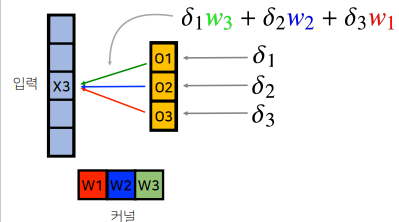
3) 해당 미분값과 입력값 x3의 곱을 커널에 전달함
4) 각 커널에 들어오는 gradient를 더하면 결국 convoution 연산과 같음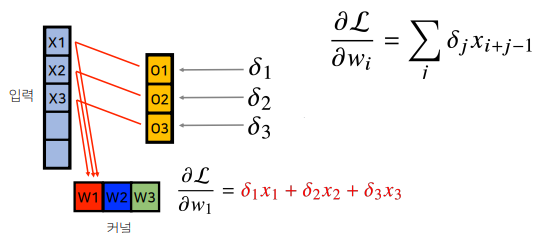

10강. RNN 첫걸음

아래에서 소개할 내용을 RNN의 기초를 다루고, 실제 데이터를 분석할 떄에는 사용하지 않는다. 실제로는 vanishing gradient 문제의 해결을 위해 LSTM/GRU 등의 모델을 사용한다.

RNN은 Recurrent neural network의 약자로, 소리/문자열/주가 등의 시퀀스(sequence) 데이터를 다룬다. 이전 시점의 데이터를 가지고다음 시점의 데이터를 예측하는데, 이때 조건부 확률을 이용한다.

\begin{aligned} P\left(X_{1}, \ldots, X_{t}\right) &=P\left(X_{t} \mid X_{1}, \ldots, X_{t-1}\right) P\left(X_{1}, \ldots, X_{t-1}\right) \\ &=P\left(X_{t} \mid X_{1}, \ldots, X_{t-1}\right) P\left(X_{t-1} \mid X_{1}, \ldots, X_{t-2}\right) P\left(X_{1}, \ldots, X_{t-2}\right)\\ &=\prod_{s=1}^{t} P\left(X_{s} \mid X_{s-1}, \ldots, X_{1}\right) \end{aligned}

정리하면 특정 시점의 데이터는 이전 시점의 데이터를 이용하게 되는데, 이 경우 아래와 같이 조건부에 들어가는 데이터의 길이가 가변적이다.

\begin{gathered} X_{t} \sim P\left(X_{t} \mid X_{t-1}, \ldots, X_{1}\right) \\ X_{t+1} \sim P\left(X_{t+1} \mid X_{t}, X_{t-1}, \ldots, X_{1}\right) \end{gathered}

이 문제를 해결하기 위해 이전 시퀀스의 정보중 고정된 길이 만큼의 시퀀스만 사용하는 자기회귀모델(Autoregressive Model) 과 바로이전정보를 제외한 나머지 정보를 $H_t$ 라는 잠재변수로 인코딩해서 사용하는 잠재 AR모델이 있다.

RNN은 잠재변수 $H_t$ 을 신경망을 통해 반복해서 사용하여 시퀀스 데이터의 패턴을 학습하는 모델이다.
RNN은 이전 순서의 잠재변수와 현재의 입력을 활용하여 모델링하며, RNN의 역전파는 잠재변수의 연결그래프에 따라 순차적으로 계산한다. 이를 Backpropagation Through Time (BPTT)라고 한다.

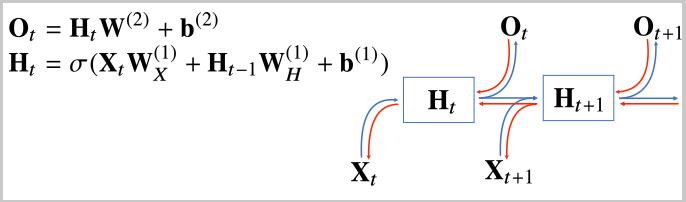
RNN의 역전파

시퀀스의 길이가 길어지는 경우 BPTT를 통한 역전파 알고리즘을 계산하면 시퀀스 처음부터 끝까지 모든 에러를 미분하여 전달해야하는데, 이경우 계산이 불안정해서 gradient vanishing 문제가 나타날 수 있다. 따라서 길이를 끊는것이 필요한데, 현재 시점에서 일정 시간 이상까지만 에러를 미분하는 back propagation을 사용하며, 이를 truncated BPTT라고 한다.

이런 문제를 해결하기 위해 등장한 것이 LSTM과 GRU이다.

과제 수행 과정 및 결과

없음

피어 세션

베이즈정리에서 evidence를 구할 때 조건부확률과 marginal distribution을 이용해서 p(D)를 구하는 과정에 대한 토의

\sum 안의 식을 정리하면 D와 theta의 교집합이 되고, 이때 marginal distribution에서 하는 것처럼 모든 theta에 대해서 그 값을 더하니까 결국 D에 대한 분포(확률)을 구한다고 이해
// 조건부확률 정의와 theta가 binary하다는 점을 생각하면 결론적으로 D와 theta의 교집합과 차집합의 합이 되는데, 이를 합한 것이 D가 됨이 자명하기 때문에 맞다.
Convolution 연산 수식에 대한 이해

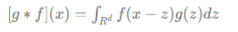
-> f가 데이터를 의미하고 z가 커널을 의미함, 커널이 f를 돌아다니며 합성곱을 하게 되는데 이때 g는 항상 고정된 index지만 f의 인덱스가 변하게 되므로 x-z라고 표현한 것
convolution 역전파에 대한 토의
순전파때 곱해준 순서 그대로 커널까지 미분값을 곱해준다.
주말에 선택과제 다 해보기